斐波那契数列的多种解法 C++实现，绘图部分用Python实现

flyfish

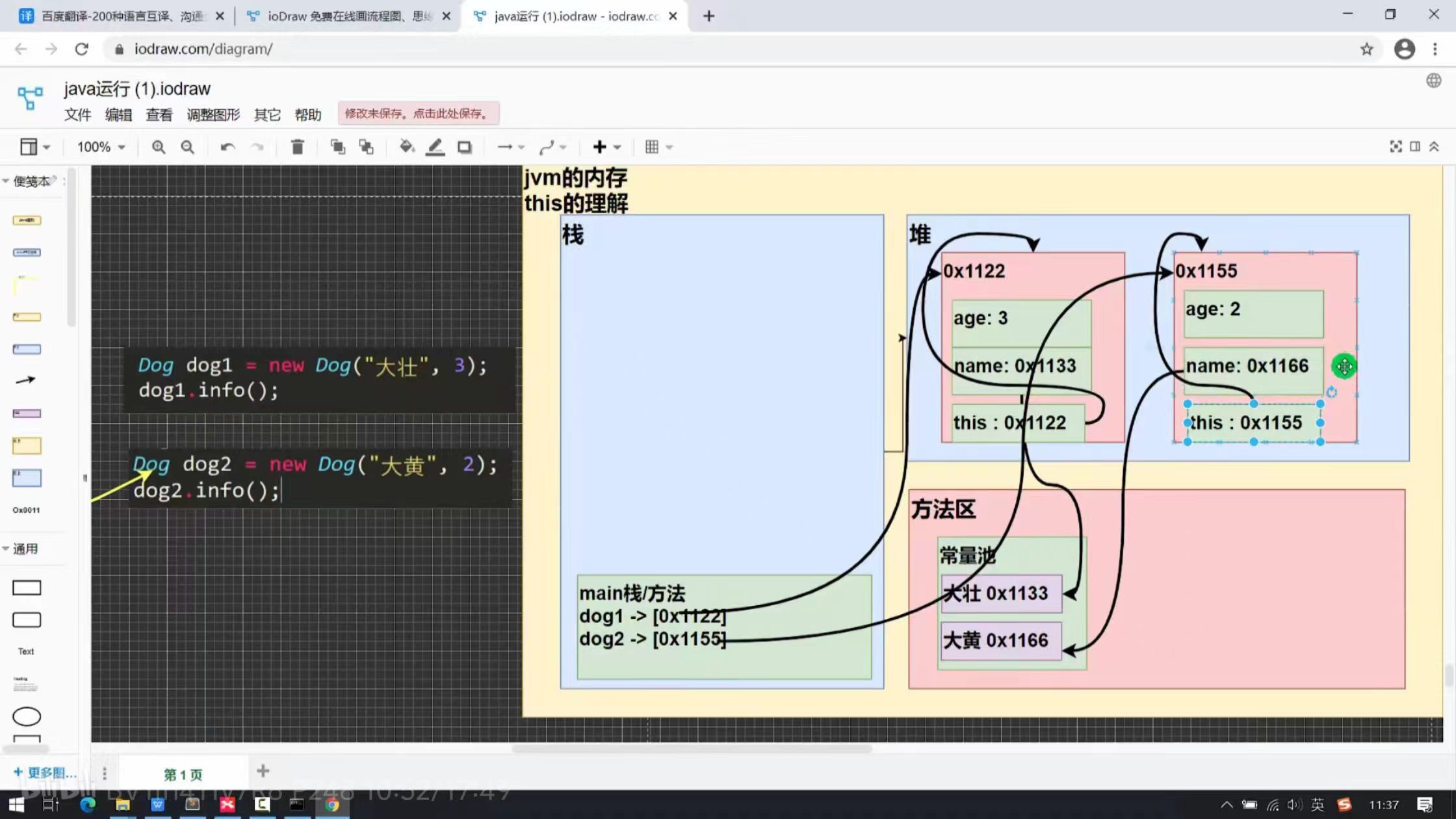
斐波那契数列（Fibonacci sequence）是一个经典的数列，定义如下：
$$\{\begin{array}{ll}0& \text{if }n=0\\ 1& \text{if }n=1\\ F(n-1)+F(n-2)& \text{if }n>1\end{array}$$
斐波那契数列由0和1开始，之后的斐波那契数就是由之前的两数相加而得出。首几个斐波那契数是：1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89
斐波那契数列的多种解法

1. 递归法

递归是最直观的方法，但它的时间复杂度很高，是指数级别 $O(2^n)$。

#include <iostream>

// 递归法计算斐波那契数列
int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

int main() {
    int n = 10;
    std::cout << "Fibonacci number at position " << n << " is " << fibonacci(n) << std::endl;
    return 0;
}

递归和递推是计算机科学和数学中解决问题的两种方法，虽然它们有些相似，但在实现和思维方式上有一些区别。下面详细解释它们的区别：

递归 (Recursion)

递归是一种解决问题的方法，其中函数通过调用自身来解决问题。递归通常包括两个部分：

1. 基本情况 (Base Case) ：定义了递归何时停止的条件。如果满足这个条件，函数将不再调用自身，直接返回结果。

2. 递归步骤 (Recursive Step) ：函数调用自身来解决一个更小的子问题。

示例：阶乘计算

阶乘是递归的经典例子。n 的阶乘（记作 n!）可以定义为：

n! = 1 当 n = 0 或 n = 1
n! = n * (n-1)! 当 n > 1

int factorial(int n) {
    if (n <= 1) return 1; // 基本情况
    else return n * factorial(n - 1); // 递归步骤
}

递推 (Iteration)

递推（也称为迭代）是一种通过重复执行某个过程的方式来解决问题的方法。在递推中，通常使用循环结构（如 for 循环或 while 循环）来重复执行某些操作，直到满足某个条件。

示例：阶乘计算

使用递推计算阶乘：

int factorial(int n) {
    int result = 1;
    for (int i = 1; i <= n; ++i) {
        result *= i;
    }
    return result;
}

2. 动态规划法

动态规划通过存储子问题的解来避免重复计算，大大提高了效率。其时间复杂度为 $O(n)$，空间复杂度也为 $O(n)$。

#include <iostream>
#include <vector>

// 动态规划法计算斐波那契数列
int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    std::vector<int> fib(n + 1);
    fib[0] = 0;
    fib[1] = 1;
    for (int i = 2; i <= n; ++i) {
        fib[i] = fib[i - 1] + fib[i - 2];
    }
    return fib[n];
}

int main() {
    int n = 10;
    std::cout << "Fibonacci number at position " << n << " is " << fibonacci(n) << std::endl;
    return 0;
}

3. 动态规划法（优化空间复杂度）

通过只保存最近两个斐波那契数，可以将空间复杂度优化为 $O(1)$。

#include <iostream>

// 优化空间复杂度的动态规划法计算斐波那契数列
int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    int a = 0, b = 1;
    for (int i = 2; i <= n; ++i) {
        int next = a + b;
        a = b;
        b = next;
    }
    return b;
}

int main() {
    int n = 10;
    std::cout << "Fibonacci number at position " << n << " is " << fibonacci(n) << std::endl;
    return 0;
}

4. 矩阵快速幂法

利用矩阵快速幂法可以将斐波那契数列的计算时间复杂度降低到 $O(\log n)$。

#include <iostream>
#include <vector>

// 矩阵乘法
std::vector<std::vector<int>> matrixMultiply(const std::vector<std::vector<int>>& a, const std::vector<std::vector<int>>& b) {
    std::vector<std::vector<int>> result(2, std::vector<int>(2));
    for (int i = 0; i < 2; ++i) {
        for (int j = 0; j < 2; ++j) {
            result[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
        }
    }
    return result;
}

// 矩阵快速幂
std::vector<std::vector<int>> matrixPower(std::vector<std::vector<int>> base, int exponent) {
    std::vector<std::vector<int>> result = {{1, 0}, {0, 1}};
    while (exponent > 0) {
        if (exponent % 2 == 1) {
            result = matrixMultiply(result, base);
        }
        base = matrixMultiply(base, base);
        exponent /= 2;
    }
    return result;
}

// 矩阵快速幂法计算斐波那契数列
int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    std::vector<std::vector<int>> F = {{1, 1}, {1, 0}};
    F = matrixPower(F, n - 1);
    return F[0][0];
}

int main() {
    int n = 10;
    std::cout << "Fibonacci number at position " << n << " is " << fibonacci(n) << std::endl;
    return 0;
}

矩阵表示法

斐波那契数列的递推关系是：

$$F(n)=F(n-1)+F(n-2)$$

可以将其表示为矩阵形式：

$$\left(\begin{array}{c}F(n)\\ F(n-1)\end{array}\right)=\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}F(n-1)\\ F(n-2)\end{array}\right)$$

令矩阵 $A$ 为：

$$A=\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)$$

那么上面的递推关系可以表示为：
$$\left(\begin{array}{c}F(n)\\ F(n-1)\end{array}\right)=A\left(\begin{array}{c}F(n-1)\\ F(n-2)\end{array}\right)$$

通过递推，可以得到：

$$\left(\begin{array}{c}F(n)\\ F(n-1)\end{array}\right)=A^{n-1}\left(\begin{array}{c}F(1)\\ F(0)\end{array}\right)$$

因为 $F(1)=1$ 和 $F(0)=0$，有：

$$\left(\begin{array}{c}F(n)\\ F(n-1)\end{array}\right)=A^{n-1}\left(\begin{array}{c}1\\ 0\end{array}\right)$$

矩阵快速幂法 高效地计算矩阵 $A^{n-1}$，使用矩阵快速幂法。矩阵快速幂法类似于普通的快速幂法，通过将幂次分解成二进制来减少计算次数。

时间复杂度分析

分析矩阵快速幂法的时间复杂度，分为以下几个步骤：

1. 矩阵乘法的时间复杂度 ：

• 矩阵乘法（两个 $2\times 2$ 矩阵相乘）的时间复杂度是 $O(1)$。虽然严格来说是 $O(4)$（每个元素需要进行4次乘法和3次加法），但在渐进意义上可以视为常数时间。

2. 矩阵幂运算的时间复杂度 ：

• 矩阵快速幂的思想是将幂次 $n$ 表示成二进制，从而通过不断的平方和乘积来减少计算次数。

• 具体地，计算矩阵的 $n$ 次幂的过程中，需要进行 $\log n$ 次矩阵乘法。因为每次将指数 $n$ 减半（或者说向右移一位）会进行一次矩阵乘法，最多需要进行 $\log n$ 次乘法。
  综上所述，矩阵快速幂法的时间复杂度主要取决于矩阵乘法的次数，而每次矩阵乘法的复杂度是 $O(1)$。因此，总的时间复杂度是：$O(\log n)$

矩阵快速幂法的时间复杂度计算

通过以下步骤来更详细地理解这一过程：

1. 初始化单位矩阵：

初始化单位矩阵的时间复杂度是 $O(1)$，因为只是创建一个 $2\times 2$ 的矩阵。

2. 矩阵乘法：

对于每次乘法操作，两矩阵相乘需要常数时间 $O(1)$。

3. 快速幂运算：

每次运算中，如果当前幂次为奇数，需要额外进行一次乘法，否则仅需要进行一次平方操作。总的乘法次数不超过 $\log n$ 次。

具体例子：

假设需要计算 $F(10)$：

1. 初始化矩阵 $A=\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)$。

2. 计算 $A^9$（因为 $F(10)=A^9\left(\begin{array}{c}1\\ 0\end{array}\right)$）。

计算过程中：

• 9 的二进制表示是 1001。

• 需要进行矩阵乘法和平方运算：

  • $A\to A^2\to A^4\to A^8$。

  • 最后，将所有奇次幂结果相乘：$A^8\cdot A$。
    总的运算次数为 $\log 9=4$ 次（近似）。

5. 通项公式法（Binet公式）

利用斐波那契数列的通项公式，直接计算第 $n$ 项的值。这个方法的时间复杂度是 $O(1)$，但由于浮点运算可能会有精度误差。
斐波那契数列的通项公式如下：
$$F(n)=\frac{1}{\sqrt{5}}\left({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n\right)$$

#include <iostream>
#include <cmath>

// 通项公式法计算斐波那契数列
int fibonacci(int n) {
    double phi = (1 + std::sqrt(5)) / 2;
    return std::round((std::pow(phi, n) - std::pow(1 - phi, n)) / std::sqrt(5));
}

int main() {
    int n = 10;
    std::cout << "Fibonacci number at position " << n << " is " << fibonacci(n) << std::endl;
    return 0;
}

斐波那契数列的通项公式可以通过特征方程法推导出来。斐波那契数列定义为：
$F(n)=F(n-1)+F(n-2)$
$F(0)=0$
$F(1)=1$
可以通过以下步骤推导出斐波那契数列的通项公式：

1). 设定递推关系的特征方程

考虑斐波那契数列的递推关系：
$F(n)-F(n-1)-F(n-2)=0$
假设其特征方程为：
$x^2-x-1=0$

2). 解特征方程

解特征方程：
$x^2-x-1=0$
使用求根公式：
$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$其中 $a=1$, $b=-1$, $c=-1$。代入公式：$x=\frac{1\pm \sqrt{5}}{2}$
得到两个根：
$\alpha =\frac{1+\sqrt{5}}{2}$
$\beta =\frac{1-\sqrt{5}}{2}$

3). 建立通解

因为这是一个二阶线性齐次递推关系，其通解形式为：
$F(n)=A{\alpha }^n+B{\beta }^n$

4). 确定常数 A 和 B

利用初始条件 $F(0)=0$ 和 $F(1)=1$，可以求解常数 $A$ 和 $B$。对于 $F(0)=0$：$A{\alpha }^0+B{\beta }^0=A+B=0$
$A=-B$对于 $F(1)=1$：$A{\alpha }^1+B{\beta }^1=A\alpha +B\beta =1$将 $A=-B$ 代入上式：$-B\alpha +B\beta =1$
$B(\beta -\alpha )=1$
$B=\frac{1}{\beta -\alpha }$因为 $\alpha$ 和 $\beta$ 的值已知，计算 $\beta -\alpha$：$\beta -\alpha =\frac{1-\sqrt{5}}{2}-\frac{1+\sqrt{5}}{2}=-\sqrt{5}$
所以：
$B=\frac{1}{-\sqrt{5}}=-\frac{1}{\sqrt{5}}$
$A=-B=\frac{1}{\sqrt{5}}$

5). 得出通项公式

将 $A$ 和 $B$ 带入通解公式：$F(n)=\frac{1}{\sqrt{5}}{\alpha }^n-\frac{1}{\sqrt{5}}{\beta }^n$
$F(n)=\frac{1}{\sqrt{5}}\left({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n\right)$

6). 最终通项公式

因此，斐波那契数列的通项公式为：
$F(n)=\frac{1}{\sqrt{5}}\left({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n\right)$
这个公式允许直接计算斐波那契数列中任意位置的数值，而不需要递归或迭代计算。

6. 编译时计算斐波那契数列编译时计算

编译时计算（Compile-time Computation）指的是在编译阶段完成的计算，而不是在程序运行时进行.

#include <iostream>

// 通用模板：计算第N个斐波那契数
// 该模板在编译期通过递归方式计算斐波那契数
template<int N>
struct Fibonacci {
    // value表示第N个斐波那契数
    // 它通过递归调用前两个斐波那契数的和来计算
    static const int value = Fibonacci<N - 1>::value + Fibonacci<N - 2>::value;
};

// 特化模板：用于结束递归
// 当N为0时，斐波那契数为0
template<>
struct Fibonacci<0> {
    static const int value = 0;
};

// 特化模板：用于结束递归
// 当N为1时，斐波那契数为1
template<>
struct Fibonacci<1> {
    static const int value = 1;
};

int main() {
    // 在编译期计算第5个斐波那契数
    // Fibonacci<5>::value的值在编译期确定，并在运行时输出
    std::cout << "Fibonacci of 5: " << Fibonacci<5>::value << std::endl;

    // 在编译期计算第10个斐波那契数
    std::cout << "Fibonacci of 10: " << Fibonacci<10>::value << std::endl;

    return 0;
}

Fibonacci<5>::value 和 Fibonacci<10>::value 在编译时计算，编译器将这些值嵌入到生成的代码中

斐波那契数可以通过对杨辉三角形中的对角线进行求和得到

杨辉三角形简介

杨辉三角形是一个由二项式系数组成的三角形，其构造规则是：

• 第一行和最后一行的数都是1。

• 其它每个数等于它上方和左上方两个数之和。

前几行的杨辉三角形如下：

	 1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

杨辉三角形与斐波那契数列的关系

可以通过在杨辉三角形中找到斐波那契数列。具体方法是将杨辉三角形的各行的元素沿对角线相加，得到斐波那契数列的元素。例如：

	    1
       1  1
     1  2  1
   1  3  3  1
 1  4  6  4  1

沿着对角线求和的步骤如下：

• 第1个斐波那契数：1

• 第2个斐波那契数：1

• 第3个斐波那契数：1 + 1 = 2

• 第4个斐波那契数：1 + 2 = 3

• 第5个斐波那契数：1 + 3 + 1 = 5

• 第6个斐波那契数：1 + 4 + 3 = 8

• 第7个斐波那契数：1 + 5 + 6 + 1 = 13

通过这种方式，可以看到杨辉三角形的对角线上的和恰好是斐波那契数列。

黄金分割表示为 $\varphi$（希腊字母 phi），其值为：$\varphi =\frac{1+\sqrt{5}}{2}\approx 1.618033988749895$

黄金分割与斐波那契数列的关系

当斐波那契数列中的一个数除以前一个数时，商会越来越接近黄金分割 $\varphi$。具体来说，斐波那契数列中的第 $n$ 项 $F(n)$ 和第 $n-1$ 项 $F(n-1)$ 的比值：$\frac{F(n)}{F(n-1)}$随着 $n$ 的增大，这个比值会趋向于 $\varphi$。这种关系可以通过以下数学公式和渐近分析来解释。

斐波那契数列的通项公式

斐波那契数列的通项公式（Binet公式）为：
$F(n)=\frac{1}{\sqrt{5}}\left({\varphi }^n-(1-\varphi {)}^n\right)$其中 $\varphi =\frac{1+\sqrt{5}}{2}$，而 $1-\varphi =\frac{1-\sqrt{5}}{2}$ 绝对值小于1，并且随着 $n$ 增加迅速趋近于0。

比值分析

当 $n$ 很大时，$(1-\varphi {)}^n$ 趋近于零，因此可以近似为：$F(n)\approx \frac{1}{\sqrt{5}}{\varphi }^n$
从而：
$F(n-1)\approx \frac{1}{\sqrt{5}}{\varphi }^{n-1}$
因此，斐波那契数列相邻两项的比值为：
$\frac{F(n)}{F(n-1)}\approx \frac{\frac{1}{\sqrt{5}}{\varphi }^n}{\frac{1}{\sqrt{5}}{\varphi }^{n-1}}=\varphi$

可视化

如果觉得不好看，代码已经提供，自己改改画吧，用Python写的

import numpy as np
import matplotlib.pyplot as plt

# 生成斐波那契数列
def fibonacci(n):
    fib_seq = [0, 1]
    for i in range(2, n):
        fib_seq.append(fib_seq[-1] + fib_seq[-2])
    return fib_seq

# 生成斐波那契螺旋点
def fibonacci_spiral_points(n_points, scale=1):
    golden_angle = np.pi * (3 - np.sqrt(5))
    angles = np.arange(n_points) * golden_angle
    radii = scale * np.sqrt(np.arange(n_points))
    
    x = radii * np.cos(angles)
    y = radii * np.sin(angles)
    
    return x, y

# 绘制斐波那契螺旋
def plot_fibonacci_spiral(n_points=500, scale=1):
    x, y = fibonacci_spiral_points(n_points, scale)
    
    plt.figure(figsize=(10, 10))
    
    # 绘制斐波那契螺旋线
    plt.plot(x, y, linestyle='-', color='b', linewidth=1, alpha=0.6)
    
    plt.title('Fibonacci Spiral')
    plt.gca().set_aspect('equal', adjustable='box')
    plt.axis('off')
    plt.show()

# 绘制向日葵种子排列
def plot_sunflower_pattern(n_points=500, scale=1):
    x, y = fibonacci_spiral_points(n_points, scale)
    
    plt.figure(figsize=(10, 10))
    
    # 绘制向日葵种子图案
    plt.scatter(x, y, s=20, c=np.arange(n_points), cmap='hsv', alpha=0.6, edgecolors='w')
    
    plt.title('Sunflower Seed Pattern')
    plt.gca().set_aspect('equal', adjustable='box')
    plt.axis('off')
    plt.show()

# 示例用法
plot_fibonacci_spiral(n_points=500, scale=10)
plot_sunflower_pattern(n_points=1000, scale=10)