数组

最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例：

• 输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
• 输出：6
• 解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

public static int maxSubArray(int[] nums) {
    if (nums == null || nums.length == 0) {
        throw new IllegalArgumentException("Array is empty");
    }

    int n = nums.length;
    int[] dp = new int[n];
    dp[0] = nums[0];
    int maxSum = dp[0];

    for (int i = 1; i < n; i++) {
        dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
        maxSum = Math.max(maxSum, dp[i]);
    }

    return maxSum;
}

合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例：

• 输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
• 输出：[[1,6],[8,10],[15,18]]
• 解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

public static int[][] merge(int[][] intervals) {
   if (intervals == null || intervals.length == 0) {
       return new int[0][0];
   }

   // Sort intervals by starting time
   Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));

   List<int[]> merged = new LinkedList<>();
   int[] currentInterval = intervals[0];
   merged.add(currentInterval);

   for (int i = 1; i < intervals.length; i++) {
       int[] interval = intervals[i];
       // If the current interval overlaps with the new interval
       if (currentInterval[1] >= interval[0]) {
           // Merge the current interval with the new interval
           currentInterval[1] = Math.max(currentInterval[1], interval[1]);
       } else {
           // If no overlap, add the current interval to the result
           // and start a new interval
           currentInterval = interval;
           merged.add(currentInterval);
       }
   }

   return merged.toArray(new int[merged.size()][]);
}

轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例：

• 输入: nums = [1,2,3,4,5,6,7], k = 3
• 输出: [5,6,7,1,2,3,4]
• 解释:

向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

public class ArrayRotation {

    // 向右轮转数组
    public static void rotate(int[] nums, int k) {
        int n = nums.length;
        if (n == 0 || k % n == 0) {
            return; // 如果数组为空或 k 是数组长度的倍数，则不需要旋转
        }
        k = k % n; // 处理 k 大于数组长度的情况
        
        reverse(nums, 0, n - 1); // 反转整个数组
        reverse(nums, 0, k - 1); // 反转前 k 个元素
        reverse(nums, k, n - 1); // 反转后 n - k 个元素
    }
    
    // 反转数组的部分
    private static void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }
}

除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例：

• 输入: nums = [1,2,3,4]
• 输出: [24,12,8,6]

public class ProductArray {

    // 计算除自身以外的数组乘积
    public static int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] leftProducts = new int[n];
        int[] rightProducts = new int[n];
        int[] result = new int[n];

        // 计算左侧乘积
        leftProducts[0] = 1;
        for (int i = 1; i < n; i++) {
            leftProducts[i] = leftProducts[i - 1] * nums[i - 1];
        }

        // 计算右侧乘积
        rightProducts[n - 1] = 1;
        for (int i = n - 2; i >= 0; i--) {
            rightProducts[i] = rightProducts[i + 1] * nums[i + 1];
        }

        // 计算结果数组
        for (int i = 0; i < n; i++) {
            result[i] = leftProducts[i] * rightProducts[i];
        }

        return result;
    }
}

缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

示例：

• 输入：nums = [3,4,-1,1]
• 输出：2
• 解释：1 在数组中，但 2 没有。

public static int firstMissingPositive(int[] nums) {
    int n = nums.length;

    // 标记所有小于等于 0 或大于 n 的数为 n + 1
    for (int i = 0; i < n; i++) {
        if (nums[i] <= 0 || nums[i] > n) {
            nums[i] = n + 1;
        }
    }

    // 将每个正整数映射到对应的索引位置
    for (int i = 0; i < n; i++) {
        int num = Math.abs(nums[i]);
        if (num <= n) {
            nums[num - 1] = -Math.abs(nums[num - 1]);
        }
    }

    // 查找第一个未出现的正整数
    for (int i = 0; i < n; i++) {
        if (nums[i] > 0) {
            return i + 1;
        }
    }

    // 如果所有 1 到 n 的正整数都出现了，则返回 n + 1
    return n + 1;
}

矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例：

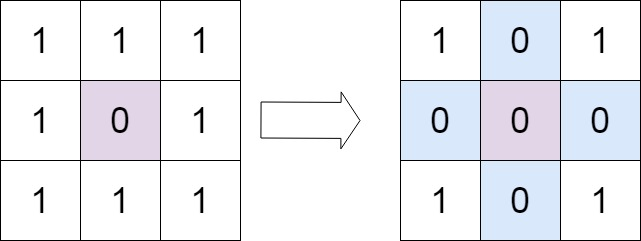
• 输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
• 输出：[[1,0,1],[0,0,0],[1,0,1]]

public class MatrixZeroes {
    public static void setZeroes(int[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return;
        }

        int m = matrix.length;
        int n = matrix[0].length;
        boolean firstRowZero = false;
        boolean firstColZero = false;

        // Check if the first row needs to be zeroed
        for (int j = 0; j < n; j++) {
            if (matrix[0][j] == 0) {
                firstRowZero = true;
                break;
            }
        }

        // Check if the first column needs to be zeroed
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                firstColZero = true;
                break;
            }
        }

        // Use the first row and first column as markers
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0; // Mark the row
                    matrix[0][j] = 0; // Mark the column
                }
            }
        }

        // Zero out cells based on markers in the first row and first column
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }

        // Zero out the first row if needed
        if (firstRowZero) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }

        // Zero out the first column if needed
        if (firstColZero) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

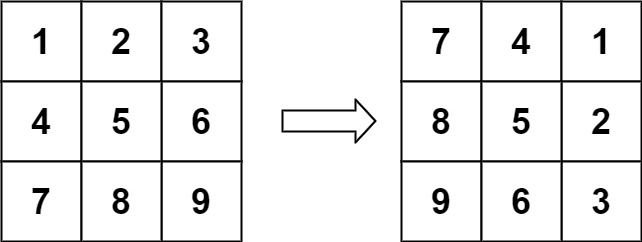
旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例：

public void rotate(int[][] matrix) {
    int n = matrix.length;
    
    // Step 1: 转置矩阵
    for (int i = 0; i < n; i++) {
        for (int j = i; j < n; j++) {
            // 交换 matrix[i][j] 和 matrix[j][i]
            int temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
    
    // Step 2: 反转每一行
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n / 2; j++) {
            // 交换 matrix[i][j] 和 matrix[i][n-1-j]
            int temp = matrix[i][j];
            matrix[i][j] = matrix[i][n - 1 - j];
            matrix[i][n - 1 - j] = temp;
        }
    }
}

搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例：

• 输入：nums = [4,5,6,7,0,1,2], target = 0
• 输出：4

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            // 找到目标值
            if (nums[mid] == target) {
                return mid;
            }

            // 判断哪一部分是有序的
            if (nums[left] <= nums[mid]) { // 左侧有序
                if (nums[left] <= target && target < nums[mid]) {
                    right = mid - 1; // 目标在左侧
                } else {
                    left = mid + 1; // 目标在右侧
                }
            } else { // 右侧有序
                if (nums[mid] < target && target <= nums[right]) {
                    left = mid + 1; // 目标在右侧
                } else {
                    right = mid - 1; // 目标在左侧
                }
            }
        }

        return -1; // 未找到目标值
    }
}

找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例：

• 输入：nums = [3,4,5,1,2]
• 输出：1
• 解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

class Solution {
    public int findMin(int[] nums) {
      int left = 0;
        int right = nums.length - 1;

        while (left < right) {
            int mid = left + (right - left) / 2;

            // 比较中间值与右边界值
            if (nums[mid] > nums[right]) {
                // 最小值在 mid 右侧
                left = mid + 1;
            } else {
                // 最小值在 mid 左侧或 mid 即为最小值
                right = mid;
            }
        }

        // 最终 left == right，即为最小值
        return nums[left];
    }
}

在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例：

• 输入：nums = [5,7,7,8,8,10], target = 8
• 输出：[3,4]

class Solution {
    private static int findFirstPosition(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        int result = -1;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                result = mid;
                right = mid - 1; // 继续向左查找
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return result;
    }

    // 查找目标值在数组中的结束位置
    private static int findLastPosition(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        int result = -1;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                result = mid;
                left = mid + 1; // 继续向右查找
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return result;
    }

    // 主方法，返回目标值的开始位置和结束位置
    public static int[] searchRange(int[] nums, int target) {
        int[] result = new int[2];
        result[0] = findFirstPosition(nums, target);
        result[1] = findLastPosition(nums, target);
        return result;
    }
}

搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例：

• 输入: nums = [1,3,5,6], target = 5
• 输出: 2

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return left;
    }
}

寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

示例：

• 输入：nums = [3,4,5,1,2]
• 输出：1
• 解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

class Solution {
    public int findMin(int[] nums) {
        int left = 0;
        int right = nums.length - 1;

        while (left < right) {
            int mid = left + (right - left) / 2;

            // 比较中间元素和右端元素
            if (nums[mid] > nums[right]) {
                // 最小值在右半部分
                left = mid + 1;
            } else {
                // 最小值在左半部分或者是 mid
                right = mid;
            }
        }

        // 最小值在 left 或 right 位置
        return nums[left];
    }
}

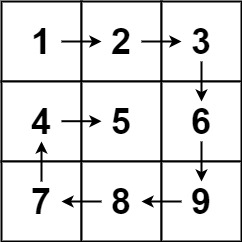
螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例：

public static List<Integer> spiralOrder(int[][] matrix) {
    List<Integer> result = new ArrayList<>();
    if (matrix == null || matrix.length == 0) {
        return result;
    }

    int m = matrix.length;
    int n = matrix[0].length;
    int left = 0, right = n - 1, top = 0, bottom = m - 1;

    while (left <= right && top <= bottom) {
        // 从左到右遍历上边界
        for (int i = left; i <= right; i++) {
            result.add(matrix[top][i]);
        }
        top++; // 上边界下移

        // 从上到下遍历右边界
        for (int i = top; i <= bottom; i++) {
            result.add(matrix[i][right]);
        }
        right--; // 右边界左移

        // 确保还有下边界要遍历
        if (top <= bottom) {
            // 从右到左遍历下边界
            for (int i = right; i >= left; i--) {
                result.add(matrix[bottom][i]);
            }
            bottom--; // 下边界上移
        }

        // 确保还有左边界要遍历
        if (left <= right) {
            // 从下到上遍历左边界
            for (int i = bottom; i >= top; i--) {
                result.add(matrix[i][left]);
            }
            left++; // 左边界右移
        }
    }

    return result;
}

反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

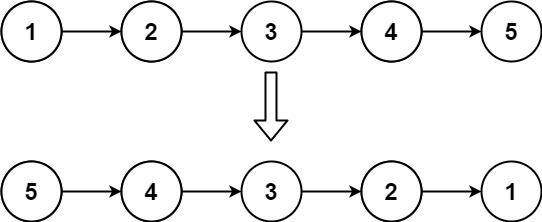
• 输入：head = [1,2,3,4,5]
• 输出：[5,4,3,2,1]

class ListNode {
    int val;
    ListNode next;
    ListNode(int x) { val = x; }
}

public class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        
        while (curr != null) {
            ListNode temp = curr.next; // 保存下一个节点
            curr.next = prev;              // 当前节点的next指向前一个节点
            prev = curr;                   // 前一个节点移到当前节点
            curr = temp;               // 当前节点移到下一个节点
        }
        
        return prev;
    }
}

两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例：

• 输入：head = [1,2,3,4]
• 输出：[2,1,4,3]

public ListNode swapPairs(ListNode head) {
   // 1. 创建一个哑节点，简化边界情况处理
   ListNode dummy = new ListNode(0);
   dummy.next = head;
   ListNode prev = dummy;

   while (prev.next != null && prev.next.next != null) {
       // 2. 标记要交换的两个节点
       ListNode first = prev.next;
       ListNode second = prev.next.next;

       // 3. 交换节点
       first.next = second.next;
       second.next = first;
       prev.next = second;

       // 4. 移动到下一个节点对
       prev = first;
   }

   return dummy.next;
}

删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例：

• 输入：head = [1,2,3,4,5], n = 2
• 输出：[1,2,3,5]

public ListNode removeNthFromEnd(ListNode head, int n) {
   // 1. 创建一个哑节点，简化边界情况处理
   ListNode dummy = new ListNode(0);
   dummy.next = head;
   ListNode first = dummy;
   ListNode second = dummy;
   
   // 2. 让 first 指针先移动 n+1 步
   for (int i = 0; i < n + 1; i++) {
       first = first.next;
   }

   // 3. 同时移动 first 和 second 指针，直到 first 到达链表末尾
   while (first != null) {
       first = first.next;
       second = second.next;
   }

   // 4. 删除倒数第 n 个节点
   second.next = second.next.next;

   // 返回链表的头节点
   return dummy.next;
}

两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例1：

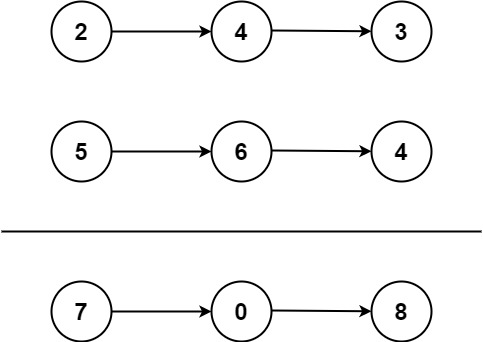
• 输入：l1 = [2,4,3], l2 = [5,6,4]
• 输出：[7,0,8]
• 解释：342 + 465 = 807.

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    ListNode dummyHead = new ListNode(0);
    ListNode p = l1, q = l2, current = dummyHead;
    int carry = 0;
    
    while (p != null || q != null) {
        int x = (p != null) ? p.val : 0;
        int y = (q != null) ? q.val : 0;
        int sum = carry + x + y;
        carry = sum / 10;
        current.next = new ListNode(sum % 10);
        current = current.next;
        if (p != null) p = p.next;
        if (q != null) q = q.next;
    }
    
    if (carry > 0) {
        current.next = new ListNode(carry);
    }
    
    return dummyHead.next;
}

合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例1：

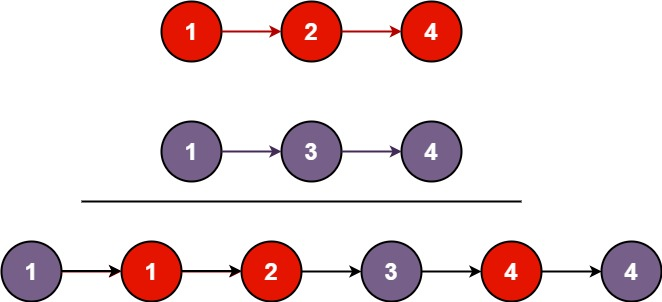
• 输入：l1 = [1,2,4], l2 = [1,3,4]
• 输出：[1,1,2,3,4,4]

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
   ListNode dummy = new ListNode(0);
   ListNode current = dummy;

   while (l1 != null && l2 != null) {
       if (l1.val < l2.val) {
           current.next = l1;
           l1 = l1.next;
       } else {
           current.next = l2;
           l2 = l2.next;
       }
       current = current.next;
   }

   if (l1 != null) {
       current.next = l1;
   } else {
       current.next = l2;
   }

   return dummy.next;
}

合并 K 个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例1：

• 输入：lists = [[1,4,5],[1,3,4],[2,6]]
• 输出：[1,1,2,3,4,4,5,6]
• 解释：链表数组如下：
  [
  1->4->5,
  1->3->4,
  2->6
  ]
  将它们合并到一个有序链表中得到。
  1->1->2->3->4->4->5->6

示例2：
输入：lists = [[]]
输出：[]

public ListNode mergeKLists(ListNode[] lists) {
   PriorityQueue<ListNode> pq = new PriorityQueue<>((a, b) -> a.val - b.val);

   // 初始化优先队列，将每个链表的第一个节点放入队列
   for (ListNode list : lists) {
       if (list != null) {
           pq.add(list);
       }
   }

   ListNode dummy = new ListNode(0);
   ListNode current = dummy;

   // 处理优先队列中的节点
   while (!pq.isEmpty()) {
       ListNode node = pq.poll();
       current.next = node;
       current = current.next;
       if (node.next != null) {
           pq.add(node.next);
       }
   }

   return dummy.next;
}

排序链表

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例1：

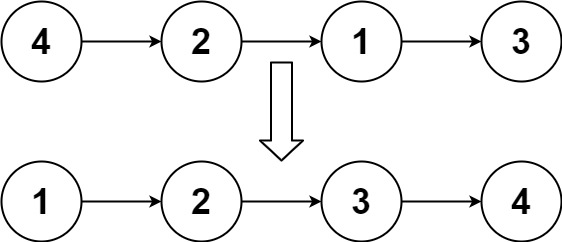
• 输入：head = [4,2,1,3]
• 输出：[1,2,3,4]

public ListNode sortList(ListNode head) {
   // 基本情况：如果链表为空或只有一个节点
   if (head == null || head.next == null) {
       return head;
   }
   
   // 找到链表的中点
   ListNode mid = getMid(head);
   ListNode left = head;
   ListNode right = mid.next;
   mid.next = null; // 将链表分为两个部分
   
   // 递归地对两个子链表进行排序
   left = sortList(left);
   right = sortList(right);
   
   // 合并排序后的子链表
   return merge(left, right);
}
    
private ListNode getMid(ListNode head) {
   ListNode slow = head;
   ListNode fast = head.next;
   while (fast != null && fast.next != null) {
       slow = slow.next;
       fast = fast.next.next;
   }
   return slow;
}
    
private ListNode merge(ListNode l1, ListNode l2) {
   ListNode dummy = new ListNode(0);
   ListNode current = dummy;
   while (l1 != null && l2 != null) {
       if (l1.val < l2.val) {
           current.next = l1;
           l1 = l1.next;
       } else {
           current.next = l2;
           l2 = l2.next;
       }
       current = current.next;
   }
   if (l1 != null) {
       current.next = l1;
   } else {
       current.next = l2;
   }
   return dummy.next;
}

相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

题目数据 保证 整个链式结构中不存在环。

示例1：

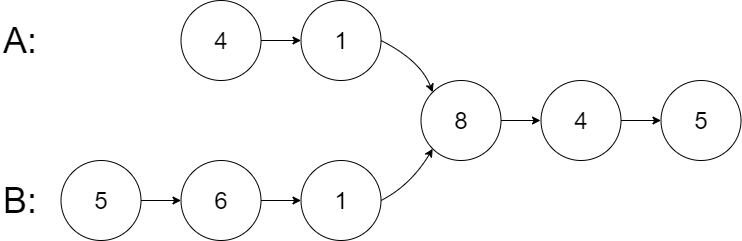
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3

输出：Intersected at ‘8’

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    // Step 1: Calculate lengths of both lists
    int lenA = getLength(headA);
    int lenB = getLength(headB);
    
    // Step 2: Adjust starting points so that they start at the same distance from end
    while (lenA > lenB) {
        headA = headA.next;
        lenA--;
    }
    
    while (lenB > lenA) {
        headB = headB.next;
        lenB--;
    }
    
    // Step 3: Compare nodes until intersection or end
    while (headA != headB) {
        headA = headA.next;
        headB = headB.next;
    }
    
    // Either headA or headB is the intersection node, or null if no intersection
    return headA;
}
    
// Helper method to calculate length of a linked list
private int getLength(ListNode node) {
    int length = 0;
    while (node != null) {
        length++;
        node = node.next;
    }
    return length;
}

环形链表

给你一个链表的头节点 head ，判断链表中是否有环，如果链表中存在环 ，则返回 true 。 否则，返回 false 。

示例1：

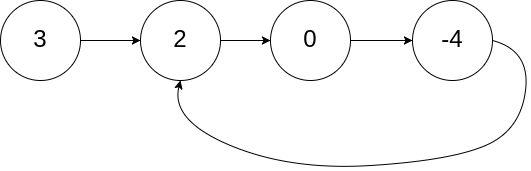
• 输入：head = [3,2,0,-4], pos = 1
• 输出：true
• 解释：链表中有一个环，其尾部连接到第二个节点。

示例2：

• 输入：head = [1], pos = -1
• 输出：false
• 解释：链表中没有环。

public boolean hasCycle(ListNode head) {
    if (head == null || head.next == null) {
        return false;
    }
    
    ListNode slow = head;
    ListNode fast = head.next;
    
    while (slow != fast) {
        if (fast == null || fast.next == null) {
            return false;
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    
    return true;
}

环形链表 II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

示例1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例2：

• 输入：head = [1], pos = -1
• 输出：返回 null
• 解释：链表中没有环。

public ListNode detectCycle(ListNode head) {
  if (head == null || head.next == null) {
      return null;
  }

  ListNode slow = head;
  ListNode fast = head;
  boolean hasCycle = false;

  // Step 1: Determine if there is a cycle
  while (fast != null && fast.next != null) {
      slow = slow.next;
      fast = fast.next.next;

      if (slow == fast) {
          hasCycle = true;
          break;
      }
  }

  // Step 2: If there is a cycle, find the start of the cycle
  if (hasCycle) {
      slow = head;
      while (slow != fast) {
          slow = slow.next;
          fast = fast.next;
      }
      return slow; // Both pointers meet at the start of the cycle
  }

  return null; // No cycle found
}

回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例1：

• 输入：head = [1,2,2,1]
• 输出：true

public boolean isPalindrome(ListNode head) {
   if (head == null || head.next == null) {
       return true;
   }

   // Step 1: Find the middle of the linked list
   ListNode slow = head;
   ListNode fast = head;
   while (fast != null && fast.next != null) {
       slow = slow.next;
       fast = fast.next.next;
   }

   // Step 2: Reverse the second half of the list
   ListNode secondHalfStart = reverseList(slow);

   // Step 3: Compare the first half and the reversed second half
   ListNode firstHalfStart = head;
   ListNode secondHalfCopy = secondHalfStart;
   while (secondHalfStart != null) {
       if (firstHalfStart.val != secondHalfStart.val) {
           return false;
       }
       firstHalfStart = firstHalfStart.next;
       secondHalfStart = secondHalfStart.next;
   }

   // Optional Step 4: Restore the list
   reverseList(secondHalfCopy);

   return true;
}

private ListNode reverseList(ListNode head) {
  ListNode prev = null;
  while (head != null) {
      ListNode next = head.next;
      head.next = prev;
      prev = head;
      head = next;
  }
  return prev;
}

两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例1：

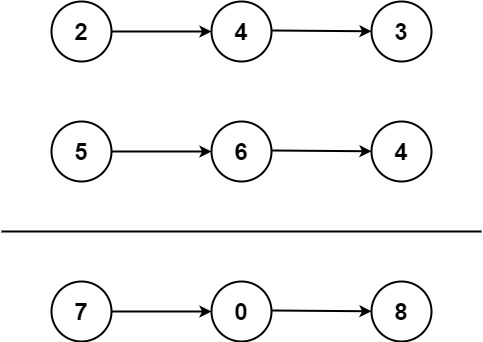
• 输入：l1 = [2,4,3], l2 = [5,6,4]
• 输出：[7,0,8]
• 解释：342 + 465 = 807.

示例2：

• 输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
• 输出：[8,9,9,9,0,0,0,1]

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
   ListNode dummyHead = new ListNode(0);
   ListNode p = l1, q = l2, curr = dummyHead;
   int carry = 0;
   while (p != null || q != null) {
       int x = (p != null) ? p.val : 0;
       int y = (q != null) ? q.val : 0;
       int sum = carry + x + y;
       carry = sum / 10;
       curr.next = new ListNode(sum % 10);
       curr = curr.next;
       if (p != null) p = p.next;
       if (q != null) q = q.next;
   }
   if (carry > 0) {
       curr.next = new ListNode(carry);
   }
   return dummyHead.next;
}

合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例1：

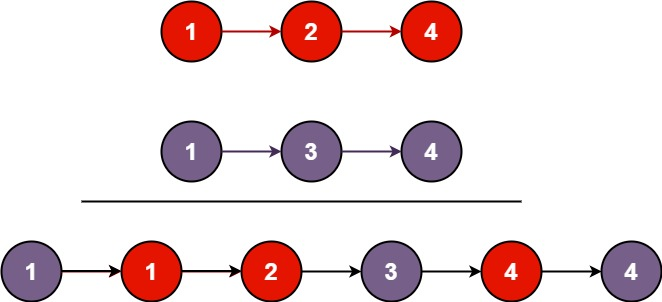
• 输入：l1 = [1,2,4], l2 = [1,3,4]
• 输出：[1,1,2,3,4,4]

示例2：

• 输入：l1 = [], l2 = []
• 输出：[]

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    ListNode dummyHead = new ListNode(0);
    ListNode curr = dummyHead;

    while (l1 != null && l2 != null) {
        if (l1.val <= l2.val) {
            curr.next = l1;
            l1 = l1.next;
        } else {
            curr.next = l2;
            l2 = l2.next;
        }
        curr = curr.next;
    }
    
    // If either l1 or l2 still has remaining elements
    if (l1 != null) {
        curr.next = l1;
    } else {
        curr.next = l2;
    }

    return dummyHead.next;
}

K 个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

示例1：

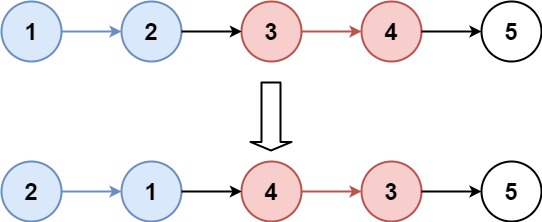
• 输入：head = [1,2,3,4,5], k = 2
• 输出：[2,1,4,3,5]

class Solution {
    private static ListNode reverseList(ListNode head, int k) {
        ListNode prev = null;
        ListNode curr = head;
        ListNode next = null;
        while (k > 0) {
            next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
            k--;
        }
        return prev;
    }

    // 计算链表的长度
    private static int getLength(ListNode head) {
        int length = 0;
        ListNode current = head;
        while (current != null) {
            length++;
            current = current.next;
        }
        return length;
    }

    // 主函数，K 个一组翻转链表
    public static ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || k <= 1) {
            return head;
        }

        int length = getLength(head);
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode prevGroupEnd = dummy;

        while (length >= k) {
            ListNode groupStart = prevGroupEnd.next;
            ListNode groupEnd = groupStart;
            for (int i = 1; i < k; i++) {
                groupEnd = groupEnd.next;
            }
            ListNode nextGroupStart = groupEnd.next;

            // 反转当前组
            groupEnd.next = null;
            prevGroupEnd.next = reverseList(groupStart, k);
            groupStart.next = nextGroupStart;

            // 移动 prevGroupEnd
            prevGroupEnd = groupStart;
            length -= k;
        }

        return dummy.next;
    }
}

随机链表的复制

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

示例：

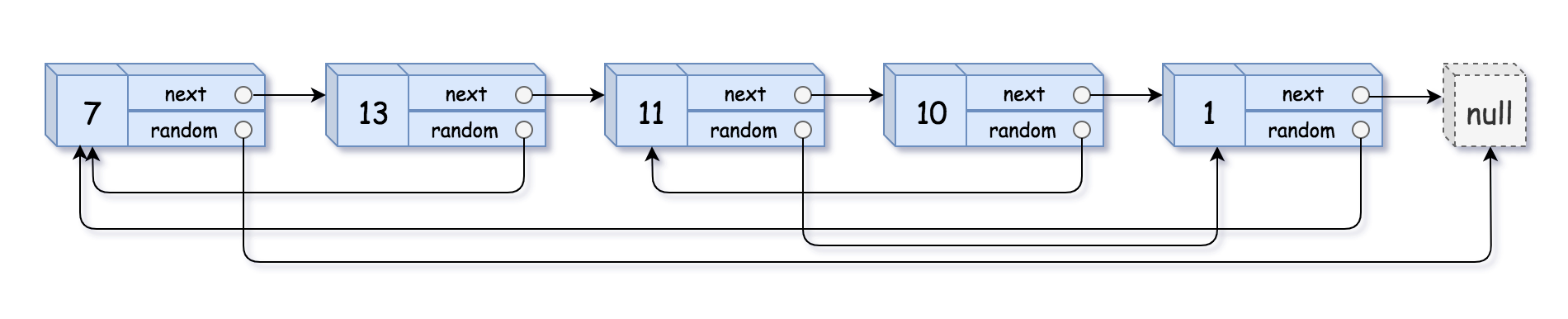
• 输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
• 输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

class Solution {
    // 复制链表
    public Node copyRandomList(Node head) {
        if (head == null) {
            return null;
        }

        // 第一遍遍历：为每个节点创建一个新节点，并将新节点插入到原节点之后
        Node current = head;
        while (current != null) {
            Node newNode = new Node(current.val);
            newNode.next = current.next;
            current.next = newNode;
            current = newNode.next;
        }

        // 第二遍遍历：设置新节点的 random 指针
        current = head;
        while (current != null) {
            Node newNode = current.next;
            newNode.random = (current.random != null) ? current.random.next : null;
            current = newNode.next;
        }

        // 第三遍遍历：分离原链表和复制链表
        Node oldHead = head;
        Node newHead = head.next;
        Node newCurrent = newHead;
        
        while (oldHead != null) {
            oldHead.next = newCurrent.next;
            oldHead = oldHead.next;
            if (oldHead != null) {
                newCurrent.next = oldHead.next;
                newCurrent = newCurrent.next;
            }
        }

        return newHead;
    }
}

树

二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例1：

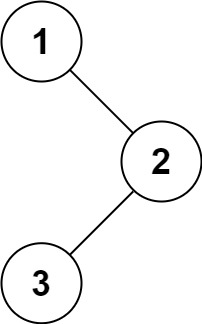
• 输入：root = [1,null,2,3]
• 输出：[1,3,2]

public List<Integer> inorderTraversal(TreeNode root) {
   List<Integer> result = new ArrayList<>();
   Stack<TreeNode> stack = new Stack<>();
   TreeNode current = root;

   while (current != null || !stack.isEmpty()) {
       // Reach the left most TreeNode
       while (current != null) {
           stack.push(current);
           current = current.left;
       }
       // Current must be null at this point
       current = stack.pop();
       result.add(current.val);  // Add the node value to the result
       current = current.right;  // Visit the right subtree
   }

   return result;
}

二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例1：

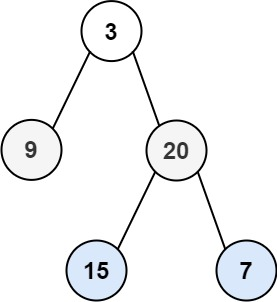
• 输入：root = [3,9,20,null,null,15,7]
• 输出：[[3],[9,20],[15,7]]

public List<List<Integer>> levelOrder(TreeNode root) {
   List<List<Integer>> result = new ArrayList<>();
   if (root == null) return result;

   Queue<TreeNode> queue = new LinkedList<>();
   queue.add(root);

   while (!queue.isEmpty()) {
       int levelSize = queue.size();
       List<Integer> currentLevel = new ArrayList<>();

       for (int i = 0; i < levelSize; i++) {
           TreeNode currentNode = queue.poll();
           currentLevel.add(currentNode.val);

           if (currentNode.left != null) {
               queue.add(currentNode.left);
           }
           if (currentNode.right != null) {
               queue.add(currentNode.right);
           }
       }

       result.add(currentLevel);
   }

   return result;
}

验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

示例1：

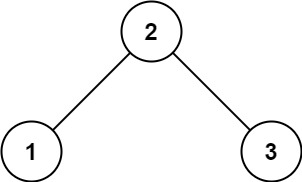
• 输入：root = [2,1,3]
• 输出：true

public boolean isValidBST(TreeNode root) {
   if (root == null) return true;
   
   Stack<TreeNode> stack = new Stack<>();
   TreeNode prev = null;
   
   while (root != null || !stack.isEmpty()) {
       while (root != null) {
           stack.push(root);
           root = root.left;
       }
       
       root = stack.pop();
       // Check current node's value with previous node
       if (prev != null && root.val <= prev.val) {
           return false;
       }
       
       prev = root;
       root = root.right;
   }
   
   return true;
}

对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例1：

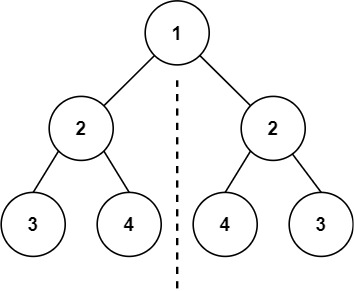
• 输入：root = [1,2,2,3,4,4,3]
• 输出：true

public boolean isSymmetric(TreeNode root) {
    if (root == null) return true;
    return isMirror(root.left, root.right);
}

private boolean isMirror(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return true;
    if (t1 == null || t2 == null) return false;
    return (t1.val == t2.val)
            && isMirror(t1.right, t2.left)
            && isMirror(t1.left, t2.right);
}

二叉树中的最大路径和

给你一个二叉树的根节点 root ，返回其 最大路径和 。

路径和 是路径中各节点值的总和。

示例1：

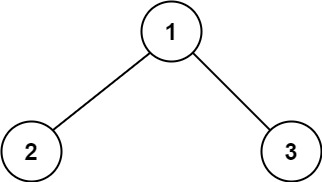
• 输入：root = [1,2,3]
• 输出：6
• 解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

int maxSum = Integer.MIN_VALUE;

public int maxPathSum(TreeNode root) {
    maxPathSumRecursive(root);
    return maxSum;
}

private int maxPathSumRecursive(TreeNode node) {
    if (node == null) return 0;
    
    // 计算左右子树的最大路径和，如果小于0则置0
    int leftSum = Math.max(maxPathSumRecursive(node.left), 0);
    int rightSum = Math.max(maxPathSumRecursive(node.right), 0);
    
    // 当前节点作为根节点的最大路径和
    int currentMax = node.val + leftSum + rightSum;
    
    // 更新全局最大路径和
    maxSum = Math.max(maxSum, currentMax);
    
    // 返回以当前节点为根节点的最大路径和（只能选左子树或右子树的一条路径）
    return node.val + Math.max(leftSum, rightSum);
}

翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例1：

• 输入：root = [4,2,7,1,3,6,9]
• 输出：[4,7,2,9,6,3,1]

public TreeNode invertTree(TreeNode root) {
    if (root == null) {
        return null;
    }
    
    // 递归翻转左右子树
    TreeNode left = invertTree(root.left);
    TreeNode right = invertTree(root.right);
    
    // 交换左右子节点
    root.left = right;
    root.right = left;
    
    return root;
}

二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例1：

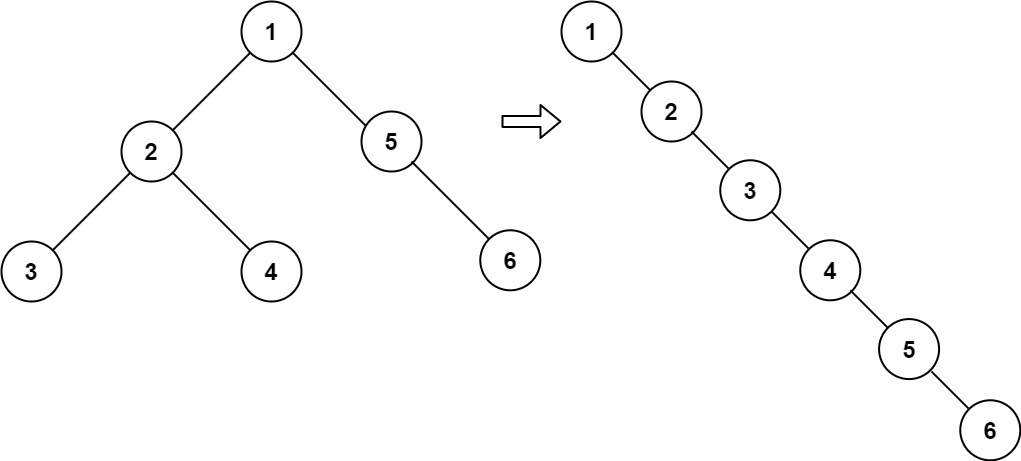
• 输入：root = [1,2,5,3,4,null,6]
• 输出：[1,null,2,null,3,null,4,null,5,null,6]

public void flatten(TreeNode root) {
   if (root == null) {
       return;
   }

   // 递归展开左子树和右子树
   flatten(root.left);
   flatten(root.right);

   // 保存右子树
   TreeNode rightSubtree = root.right;

   // 将左子树移到右子树位置
   root.right = root.left;
   root.left = null;

   // 找到新的右子树的末端
   TreeNode current = root;
   while (current.right != null) {
       current = current.right;
   }

   // 将保存的右子树接到末端
   current.right = rightSubtree;
}

技巧

颜色分类

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

示例：

• 输入：nums = [2,0,2,1,1,0]
• 输出：[0,0,1,1,2,2]

class Solution {
    public void sortColors(int[] nums) {
       int low = 0, mid = 0, high = nums.length - 1;
        
        while (mid <= high) {
            if (nums[mid] == 0) {
                // Swap nums[low] and nums[mid]
                int temp = nums[low];
                nums[low] = nums[mid];
                nums[mid] = temp;
                low++;
                mid++;
            } else if (nums[mid] == 1) {
                mid++;
            } else {
                // Swap nums[mid] and nums[high]
                int temp = nums[mid];
                nums[mid] = nums[high];
                nums[high] = temp;
                high--;
            }
        }
    }
}

多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

示例：

• 输入：nums = [3,2,3]
• 输出：3

class Solution {
    public int majorityElement(int[] nums) {
        int candidate = findCandidate(nums);
        return candidate;
    }
    
    private int findCandidate(int[] nums) {
        int candidate = nums[0];
        int count = 1;
        
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] == candidate) {
                count++;
            } else {
                count--;
                if (count == 0) {
                    candidate = nums[i];
                    count = 1;
                }
            }
        }
        
        return candidate;
    }
}

动态规划

最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

示例：

• 输入：text1 = “abcde”, text2 = “ace”
• 输出：3
• 解释：最长公共子序列是 “ace” ，它的长度为 3 。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
      int m = text1.length();
        int n = text2.length();
        
        // 创建动态规划表
        int[][] dp = new int[m + 1][n + 1];
        
        // 填充动态规划表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        
        // 返回最长公共子序列的长度
        return dp[m][n];
    }
}

完全平方数

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例：

• 输入：n = 12
• 输出：3
• 解释：12 = 4 + 4 + 4

public class PerfectSquares {

    // 计算和为 n 的完全平方数的最少数量
    public static int numSquares(int n) {
        if (n <= 0) {
            return 0;
        }

        // 初始化动态规划数组
        int[] dp = new int[n + 1];
        // 填充 dp 数组，初始值为最大值 n + 1
        for (int i = 1; i <= n; i++) {
            dp[i] = Integer.MAX_VALUE;
        }

        // 计算 dp[i] 的值
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j * j <= i; j++) {
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }

        return dp[n];
    }
}

零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

示例：

• 输入：coins = [1, 2, 5], amount = 11
• 输出：3
• 解释：11 = 5 + 5 + 1

public class CoinChange {

    // 计算组成金额 amount 的最少硬币数量
    public static int coinChange(int[] coins, int amount) {
        // 动态规划数组
        int[] dp = new int[amount + 1];
        // 初始化动态规划数组，初始值为最大值 amount + 1
        for (int i = 1; i <= amount; i++) {
            dp[i] = amount + 1;
        }
        dp[0] = 0; // 组成金额 0 不需要硬币

        // 填充动态规划数组
        for (int i = 1; i <= amount; i++) {
            for (int coin : coins) {
                if (i - coin >= 0) {
                    dp[i] = Math.min(dp[i], dp[i - coin] + 1);
                }
            }
        }

        // 返回结果
        return dp[amount] > amount ? -1 : dp[amount];
    }
}

单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例：

• 输入: s = “leetcode”, wordDict = [“leet”, “code”]
• 输出: true
• 解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。

public class WordBreak {

    // 判断字符串 s 是否可以由字典中的单词拼接而成
    public static boolean wordBreak(String s, Set<String> wordDict) {
        int n = s.length();
        // 动态规划数组
        boolean[] dp = new boolean[n + 1];
        dp[0] = true; // 空字符串可以被认为是由字典中的单词拼接而成

        // 填充动态规划数组
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                if (dp[j] && wordDict.contains(s.substring(j, i))) {
                    dp[i] = true;
                    break; // 找到一个有效的拆分后就可以停止
                }
            }
        }

        // 返回结果
        return dp[n];
    }
}

乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续
子数组
（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例：

• 输入: nums = [2,3,-2,4]
• 输出: 6
• 解释: 子数组 [2,3] 有最大乘积 6。

class Solution {
    // 找出数组中乘积最大的非空连续子数组
    public  int maxProduct(int[] nums) {
        if (nums.length == 0) return 0;

        // 初始化动态规划变量
        int maxEndingHere = nums[0];
        int minEndingHere = nums[0];
        int globalMax = nums[0];

        // 遍历数组更新动态规划变量
        for (int i = 1; i < nums.length; i++) {
            int num = nums[i];

            // 计算当前元素可能的最大乘积和最小乘积
            int tempMax = Math.max(num, Math.max(num * maxEndingHere, num * minEndingHere));
            minEndingHere = Math.min(num, Math.min(num * maxEndingHere, num * minEndingHere));

            maxEndingHere = tempMax;

            // 更新全局最大乘积
            globalMax = Math.max(globalMax, maxEndingHere);
        }

        return globalMax;
    }
}

不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例：

• 输入：m = 3, n = 2
• 输出：3
• 解释：
  从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

class Solution {
    public int uniquePaths(int m, int n) {
        // 创建一个动态规划数组
        int[][] dp = new int[m][n];
        
        // 初始化第一行和第一列
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1; // 第一列只有一种路径，即一直向下
        }
        for (int j = 0; j < n; j++) {
            dp[0][j] = 1; // 第一行只有一种路径，即一直向右
        }
        
        // 填充动态规划数组
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        
        // 返回右下角的路径数量
        return dp[m - 1][n - 1];
    }
}

最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例：

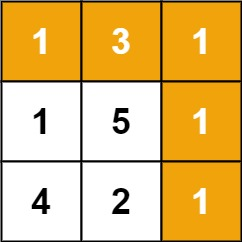
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

class Solution {
    // 计算从左上角到右下角的最小路径和
    public int minPathSum(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return 0;
        }

        int m = grid.length;
        int n = grid[0].length;

        // 创建一个动态规划数组
        int[][] dp = new int[m][n];

        // 初始化动态规划数组
        dp[0][0] = grid[0][0];

        // 初始化第一行
        for (int j = 1; j < n; j++) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }

        // 初始化第一列
        for (int i = 1; i < m; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }

        // 填充动态规划数组
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]);
            }
        }

        // 返回右下角的最小路径和
        return dp[m - 1][n - 1];
    }
}

最长回文子串

给你一个字符串 s，找到 s 中最长的 回文子串。

示例：

• 输入：s = “babad”
• 输出：“bab”
• 解释：“aba” 同样是符合题意的答案。

class Solution {
 // 找到字符串中的最长回文子串
    public static String longestPalindrome(String s) {
        if (s == null || s.length() == 0) {
            return "";
        }

        int start = 0; // 最长回文子串的起始索引
        int maxLength = 1; // 最长回文子串的长度

        for (int i = 0; i < s.length(); i++) {
            // 以 s[i] 为中心的回文子串
            String pal1 = expandAroundCenter(s, i, i);
            // 以 s[i] 和 s[i+1] 之间的间隙为中心的回文子串
            String pal2 = expandAroundCenter(s, i, i + 1);

            // 选择更长的回文子串
            String longerPal = pal1.length() > pal2.length() ? pal1 : pal2;

            if (longerPal.length() > maxLength) {
                maxLength = longerPal.length();
                start = s.indexOf(longerPal);
            }
        }

        return s.substring(start, start + maxLength);
    }

    // 扩展回文中心
    private static String expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            left--;
            right++;
        }
        return s.substring(left + 1, right);
    }

}

编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例：

• 输入：word1 = “horse”, word2 = “ros”
• 输出：3
• 解释：
  horse -> rorse (将 ‘h’ 替换为 ‘r’)
  rorse -> rose (删除 ‘r’)
  rose -> ros (删除 ‘e’)

class Solution {
    public static int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();

        // 创建动态规划数组
        int[][] dp = new int[m + 1][n + 1];

        // 初始化 dp 数组
        for (int i = 0; i <= m; i++) {
            dp[i][0] = i; // 删除操作
        }
        for (int j = 0; j <= n; j++) {
            dp[0][j] = j; // 插入操作
        }

        // 填充动态规划数组
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1]; // 字符相同，不需要额外操作
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, // 删除操作
                                                 dp[i][j - 1] + 1), // 插入操作
                                       dp[i - 1][j - 1] + 1); // 替换操作
                }
            }
        }

        // 返回将 word1 转换成 word2 的最小操作数
        return dp[m][n];
    }
}

堆，栈

前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例：

• 输入: nums = [1,1,1,2,2,3], k = 2
• 输出: [1,2]

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 统计每个元素的频率
        Map<Integer, Integer> frequencyMap = new HashMap<>();
        for (int num : nums) {
            frequencyMap.put(num, frequencyMap.getOrDefault(num, 0) + 1);
        }

        // 使用优先队列（最小堆）来维护前 k 个频率最高的元素
        PriorityQueue<Map.Entry<Integer, Integer>> minHeap = new PriorityQueue<>(
                (a, b) -> a.getValue() - b.getValue()
        );

        for (Map.Entry<Integer, Integer> entry : frequencyMap.entrySet()) {
            minHeap.add(entry);
            if (minHeap.size() > k) {
                minHeap.poll(); // 移除频率最低的元素
            }
        }

        // 将优先队列中的元素取出并放入结果数组
        int[] result = new int[k];
        for (int i = 0; i < k; i++) {
            result[i] = minHeap.poll().getKey();
        }

        return result;
    }
}

数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例：

class Solution {
    private static final Random rand = new Random();

    public static int findKthLargest(int[] nums, int k) {
        int n = nums.length;
        return quickSelect(nums, 0, n - 1, n - k);
    }

    private static int quickSelect(int[] nums, int left, int right, int index) {
        if (left == right) {
            return nums[left];
        }
        
        int pivotIndex = partition(nums, left, right);

        if (pivotIndex == index) {
            return nums[pivotIndex];
        } else if (pivotIndex < index) {
            return quickSelect(nums, pivotIndex + 1, right, index);
        } else {
            return quickSelect(nums, left, pivotIndex - 1, index);
        }
    }

    private static int partition(int[] nums, int left, int right) {
        int pivotIndex = left + rand.nextInt(right - left + 1);
        int pivotValue = nums[pivotIndex];
        swap(nums, pivotIndex, right);

        int storeIndex = left;
        for (int i = left; i < right; i++) {
            if (nums[i] < pivotValue) {
                swap(nums, storeIndex, i);
                storeIndex++;
            }
        }
        swap(nums, storeIndex, right);

        return storeIndex;
    }

    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例：

• 输入: temperatures = [73,74,75,71,69,72,76,73]
• 输出: [1,1,4,2,1,1,0,0]

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        int[] answer = new int[n];
        Stack<Integer> stack = new Stack<>();

        for (int i = 0; i < n; i++) {
            while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                int index = stack.pop();
                answer[index] = i - index;
            }
            stack.push(i);
        }

        return answer;
    }
}

最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

示例：

输入：
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

class MinStack {

private Stack<Integer> stack;
    private Stack<Integer> minStack;

    public MinStack() {
        stack = new Stack<>();
        minStack = new Stack<>();
    }

    public void push(int val) {
        stack.push(val);
        if (minStack.isEmpty() || val <= minStack.peek()) {
            minStack.push(val);
        } else {
            minStack.push(minStack.peek());
        }
    }

    public void pop() {
        stack.pop();
        minStack.pop();
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }

}

有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。
• 每个右括号都有一个对应的相同类型的左括号。

示例：

class Solution {
    public boolean isValid(String s) {
        // 使用栈来存放左括号
        Stack<Character> stack = new Stack<>();

        // 遍历字符串中的每个字符
        for (char c : s.toCharArray()) {
            // 如果是左括号，压入栈中
            if (c == '(' || c == '{' || c == '[') {
                stack.push(c);
            }
            // 如果是右括号，检查栈顶是否是对应的左括号
            else if (c == ')' && !stack.isEmpty() && stack.peek() == '(') {
                stack.pop();
            } else if (c == '}' && !stack.isEmpty() && stack.peek() == '{') {
                stack.pop();
            } else if (c == ']' && !stack.isEmpty() && stack.peek() == '[') {
                stack.pop();
            } else {
                // 如果不匹配或者栈为空，则字符串无效
                return false;
            }
        }

        // 如果栈为空，则字符串有效
        return stack.isEmpty();
    }
}