前言

本章将介绍神经网络的学习中的一些重要观点，主题涉及寻找最优权重参数的最优化方法、权重参数的初始值、超参数的设定方法等

此外，为了应对过拟合，本章还将介绍权值衰减、Dropout等正则化方法，并进行实现。

最后将对近年来众多研究中使用的Batch Normalization 方法进行简单的介绍。

使用本章介绍的方法，可以高效地进行神经网络（深度学习）的学习，提高识别精度。让我们一起往下看吧！

参数的更新

神经网络的学习的目的是找到使损失函数的值尽可能小的参数，，解决这个问题的过程称为最优化（optimization）

随机梯度下降法（stochastic gradient descent），简称SGD。SGD是一个简单的方法，不过比起胡乱地搜索参数空间，也算是“聪明”的方法

我们将指出SGD的缺点，并介绍SGD以外的其他最优化方法。

冒险家的故事

有一个性情古怪的探险家。他在广袤的干旱地带旅行，坚持寻找幽深的山谷。他的目标是要到达最深的谷底（他称之为“至深之地”）。这也是他旅行的目的。并且，他给自己制定了两个严格的“规定”：一个是不看地图；另一个是把眼睛蒙上。因此，他并不知道最深的谷底在这个广袤的大地的何处，而且什么也看不见。在这么严苛的条件下，这位探险家如何前往“至深之地”呢？他要如何迈步，才能迅速找到“至深之地”呢？

在这么困难的状况下，地面的坡度显得尤为重要。探险家虽然看不到周围的情况，但是能够知道当前所在位置的坡度（通过脚底感受地面的倾斜状况）。于是，朝着当前所在位置的坡度最大的方向前进，就是SGD的策略。勇敢的探险家心里可能想着只要重复这一策略，总有一天可以到达“至深之地”。

SGD

这里把需要更新的权重参数记为W，把损失函数关于W的梯度记为
$$\frac{\partial L}{\partial W}$$
η 表示学习率，实际上会取0.01 或0.001 这些事先决定好的值

式子中的←表示用右边的值更新左边的值

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

使用这个SGD类，可以按如下方式进行神经网络的参数的更新（下面的代码是不能实际运行的伪代码）。

network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
    ...
    x_batch, t_batch = get_mini_batch(...) # mini-batch
    grads = network.gradient(x_batch, t_batch)
    params = network.params
    optimizer.update(params, grads)
    ...

通过单独实现进行最优化的类，功能的模块化变得更简单

[!IMPORTANT]

很多深度学习框架都实现了各种最优化方法，并且提供了可以简单切换这些方法的构造

SGD的缺点

在指出SGD的缺点之际，我们来思考一下求下面这个函数的最小值的问题。

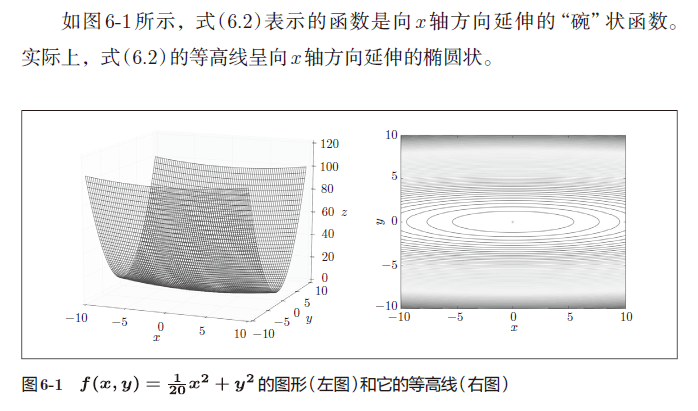
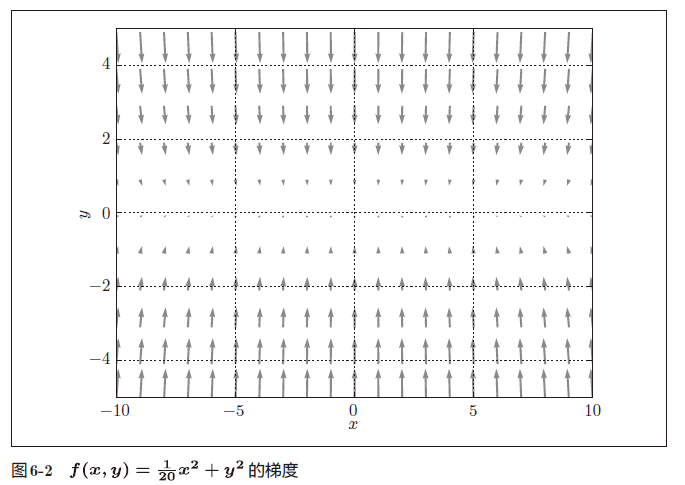
就是y 轴方向的坡度大，而x轴方向的坡度小

虽然式（6.2）的最小值在(x, y) = (0, 0) 处，但是图6-2 中的梯度在很多地方并没有指向(0, 0)。

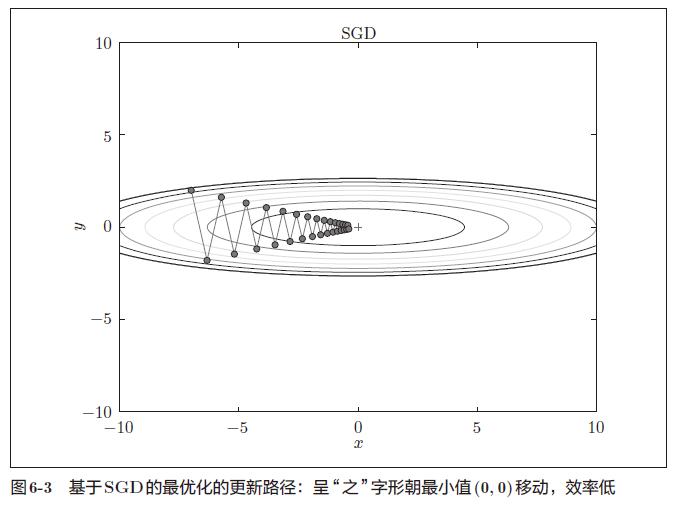
SGD的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效

我们需要比单纯朝梯度方向前进的SGD更聪明的方法。SGD低效的根本原因是，梯度的方向并没有指向最小值的方向。

Momentum

Momentum是“动量”的意思，和物理有关

W表示要更新的权重参数， 表示损失函数关于W的梯度，η 表示学习率。这里新出现了一个变量v，对应物理上的速度。式（6.3）表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加这一物理法则

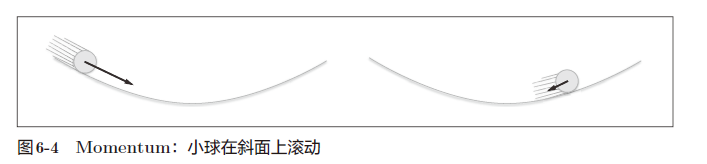
式（6.3）中有αv这一项。在物体不受任何力时，该项承担使物体逐渐减速的任务（α设定为0.9 之类的值），对应物理上的地面摩擦或空气阻力。

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
        def update(self, params, grads):
            if self.v is None:
                self.v = {}
                for key, val in params.items():
                    self.v[key] = np.zeros_like(val)
                    
            for key in params.keys():
                self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
                params[key] += self.v[key]

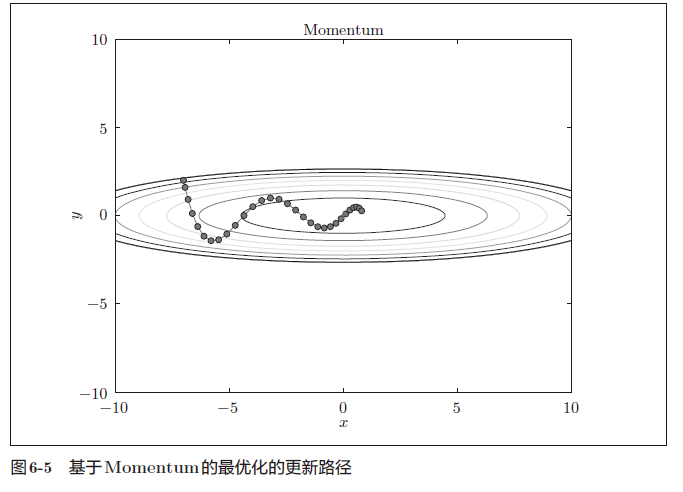
现在尝试使用Momentum解决式（6.2）的最优化问题，如图6-5 所示。

AdaGrad

在神经网络的学习中，学习率（数学式中记为η）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。

在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多”学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用。

AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习（AdaGrad的Ada来自英文单词Adaptive，即“适当的”的意思）

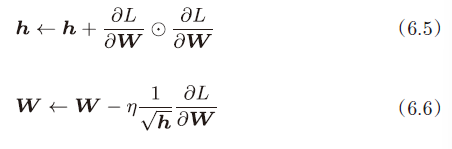
如式(6.5) 所示，它保存了以前的所有梯度值的平方和（式（6.5）中的表示⊙对应矩阵元素的乘法）

参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

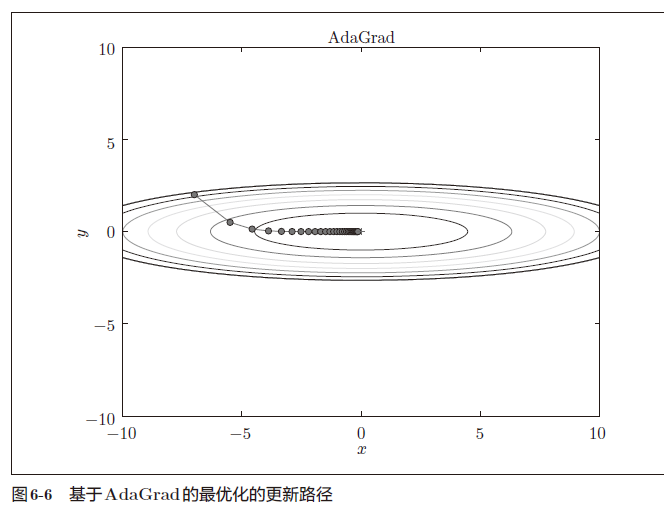
函数的取值高效地向着最小值移动

由于y 轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐

Adam

Momentum参照小球在碗中滚动的物理规则进行移动，AdaGrad为参数的每个元素适当地调整更新步伐。如果将这两个方法融合在一起会怎么样呢？这就是Adam方法的基本思路。

通过组合前面两个方法的优点，有望实现参数空间的高效搜索

进行超参数的“偏置校正”也是Adam的特征

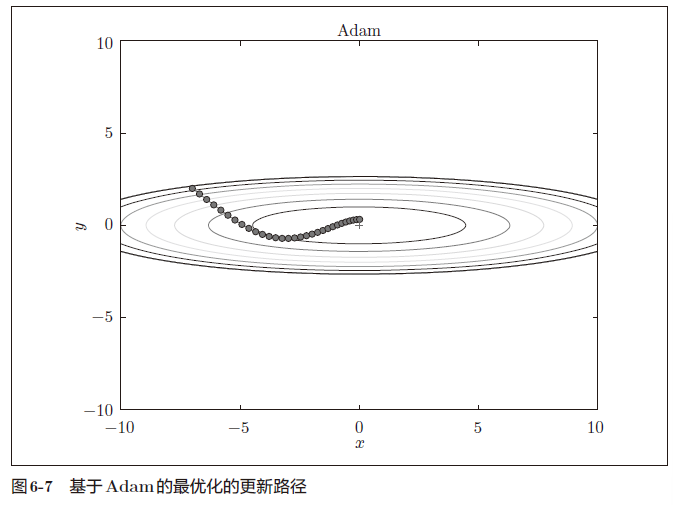
[!IMPORTANT]

Adam 会设置3 个超参数。一个是学习率（论文中以α出现），另外两个是一次momentum系数β1 和二次momentum系数β2。

使用哪种更新方法呢

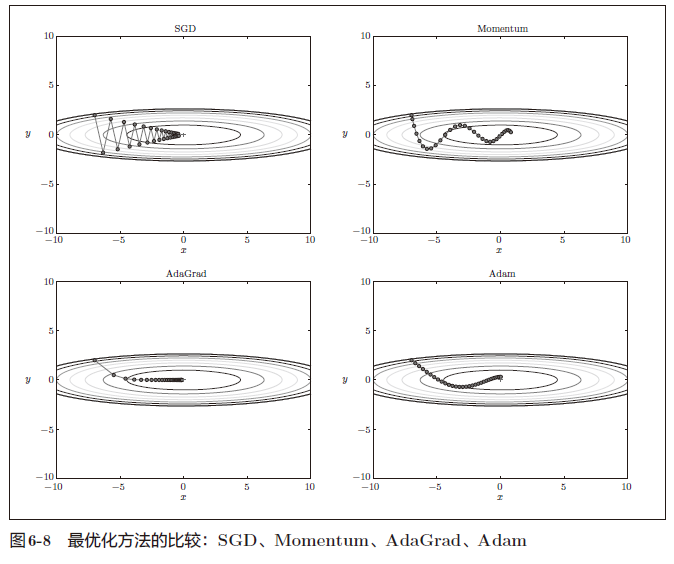
结果会根据要解决的问题而变。并且，很显然，超参数（学习率等）的设定值不同，结果也会发生变化

非常遗憾，（目前）并不存在能在所有问题中都表现良好的方法。这4 种方法各有各的特点，都有各自擅长解决的问题和不擅长解决的问题。

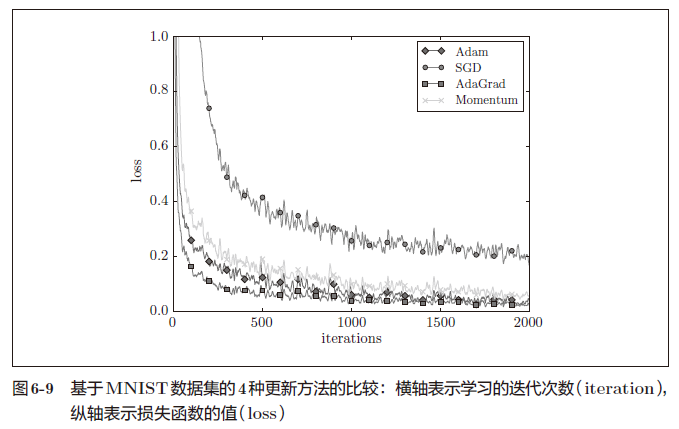
基于MNIST数据集的更新方法的比较

以手写数字识别为例，比较前面介绍的SGD、Momentum、AdaGrad、Adam这4 种方法，并确认不同的方法在学习进展上有多大程度的差异。

权重的初始值

本节将介绍权重初始值的推荐值，并通过实验确认神经网络的学习是否会快速进行

可以将权重值设为0吗

后面我们会介绍抑制过拟合、提高泛化能力的技巧——权值衰减（weight decay）。

权值衰减就是一种以减小权重参数的值为目的进行学习的方法。通过减小权重参数的值来抑制过拟合的发生。

如果我们把权重初始值全部设为0 以减小权重的值，会怎么样呢？从结论来说，将权重初始值设为0 不是一个好主意。事实上，将权重初始值设为0 的话，将无法正确进行学习。

为了防止“权重均一化”（严格地讲，是为了瓦解权重的对称结构），必须随机生成初始

隐藏层的激活值的分布

观察隐藏层的激活值（激活函数的输出数据）的分布，可以获得很多启发

来做一个简单的实验，观察权重初始值是如何影响隐藏层的激活值的分布的。这里要做的实验是，向一个5 层神经网络（激活函数使用sigmoid 函数）传入随机生成的输入数据，用直方图绘制各层激活值的数据分布

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
x = np.random.randn(1000, 100) # 1000个数据
node_num = 100 # 各隐藏层的节点（神经元）数
hidden_layer_size = 5 # 隐藏层有5层
activations = {} # 激活值的结果保存在这里
for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]
    #设定权重标准差
    w = np.random.randn(node_num, node_num) * 1
    #w = np.random.randn(node_num, node_num) * 0.01
    z = np.dot(x, w)
    a = sigmoid(z) # sigmoid函数
    activations[i] = a
    
# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

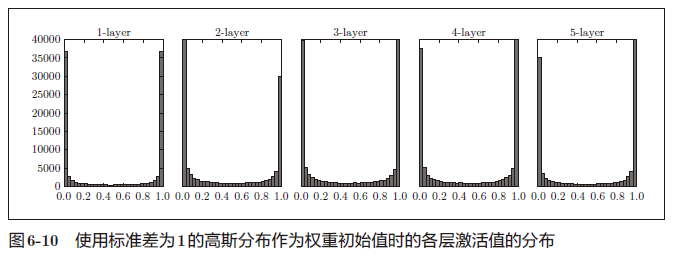
偏向0 和1 的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）

使用标准差为0.01 的高斯分布时，各层的激活值的分布如图6-11 所示。

这次呈集中在0.5 附近的分布，但是，激活值的分布有所偏向，说明在表现力上会有很大问

如果100个神经元都输出几乎相同的值，那么也可以由1 个神经元来表达基本相同的事情

激活值在分布上有所偏向会出现“表现力受限”的问题。

[!NOTE]

各层的激活值的分布都要求有适当的广度

因为通过在各层间传递多样性的数据，神经网络可以进行高效的学习

反过来，如果传递的是有所偏向的数据，就会出现梯度消失或者“表现力受限”的问题，导致学习可能无法顺利进行。

在一般的深度学习框架中，Xavier 初始值（论文中推荐的权重初始值）已被作为标准使用

$$Xavier的论文中，为了使各层的激活值呈现出具有相同广度的分布，推导了合适的权重尺度。推导出的结论是，如果前一层的节点数为n，则初始值使用标准差为\frac{1}{\sqrt{n}}的分布（图6-12）。$$

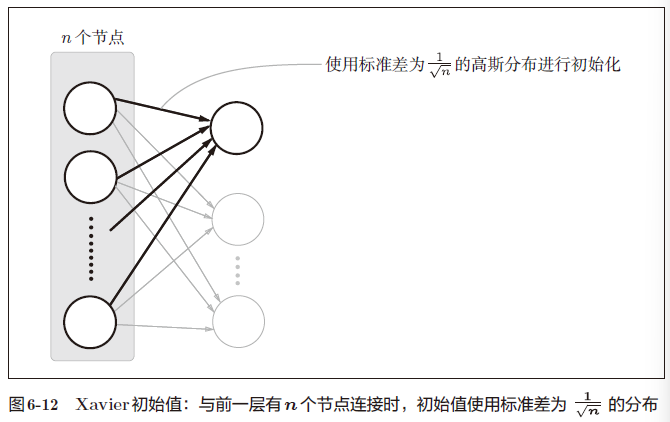
node_num = 100 # 前一层的节点数
w = np.random.randn(node_num, node_num) / np.sqrt(node_num)

使用Xavier 初始值后的结果如图6-13 所示

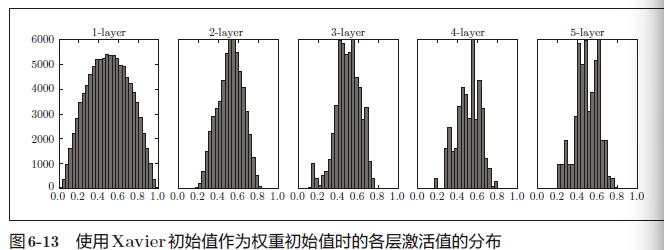
[!IMPORTANT]

图6-13 的分布中，后面的层的分布呈稍微歪斜的形状。如果用tanh函数（双曲线函数）代替sigmoid函数，这个稍微歪斜的问题就能得到改善

实际上，使用tanh函数后，会呈漂亮的吊钟型分布

众所周知，用作激活函数的函数最好具有关于原点对称的性质

ReLU的权重初始值

Xavier 初始值是以激活函数是线性函数为前提而推导出来的

当激活函数使用ReLU时，一般推荐使用ReLU专用的初始值，也就是Kaiming He等人推荐的初始值，也称为“He初始值”。
$$当前一层的节点数为n时，He初始值使用标准差为\sqrt{\frac{2}{n}}的高斯分布$$
与Xavier初始值相比较，（直观上）可以解释为，因为ReLU的负值区域的值为0，为了使它更有广度，所以需要2 倍的系数。

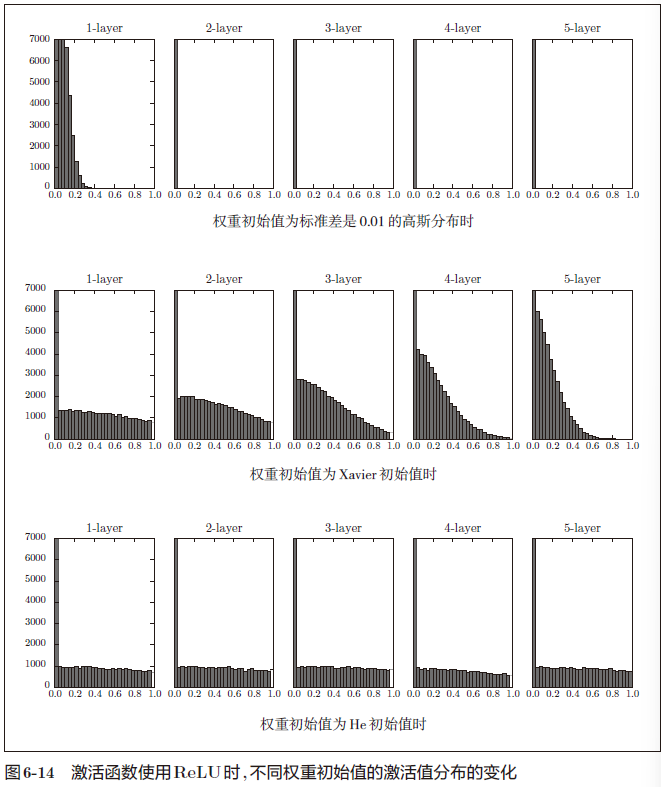
当激活函数使用ReLU时，权重初始值使用He初始值，当激活函数为sigmoid 或tanh 等S 型曲线函数时，初始值使用Xavier 初始值。这是目前的最佳实践。

基于MNIST数据集的权重初始值的比较

下面通过实际的数据，观察不同的权重初始值的赋值方法会在多大程度上影响神经网络的学习

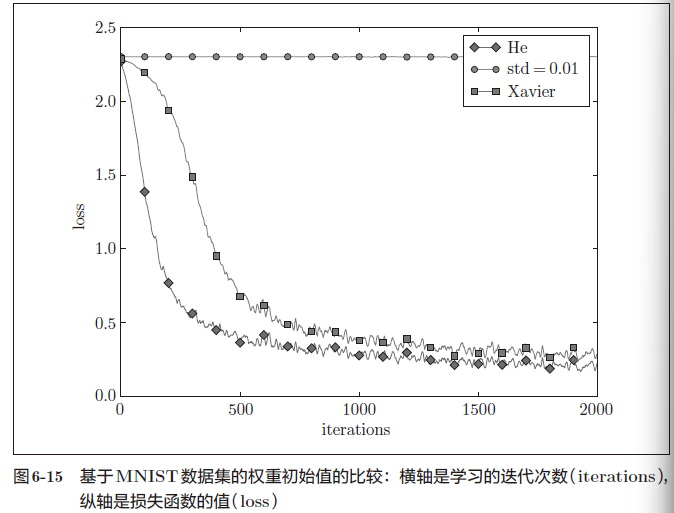
std = 0.01 时完全无法进行学习,因为正向传播中传递的值很小（集中在0附近的数据）。因此，逆向传播时求到的梯度也很小，权重几乎不进行更新。

当权重初始值为Xavier 初始值和He初始值时，学习进行得很顺利。并且，我们发现He初始值时的学习进度更快一些。

在神经网络的学习中，权重初始值非常重要。很多时候权重初始值的设定关系到神经网络的学习能否成功。

Batch Normalization

如果设定了合适的权重初始值，则各层的激活值分布会有适当的广度，从而可以顺利地进
行学习。那么，为了使各层拥有适当的广度，“强制性”地调整激活值的分布会怎样呢？实际上，Batch Normalization方法就是基于这个想法而产生的。

Batch Normalization 的算法

Batch Norm虽然是一个问世不久的新方法，但已经被很多研究人员和技术人员广泛使用

为什么Batch Norm这么惹人注目呢？因为Batch Norm有以下优点：

• 可以使学习快速进行（可以增大学习率）。
• 不那么依赖初始值（对于初始值不用那么神经质）。
• 抑制过拟合（降低Dropout等的必要性）。

Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度。为此，要向神经网络中插入对数据分布进行正规化的层，即BatchNormalization 层（下文简称Batch Norm层），如图6-16 所示。

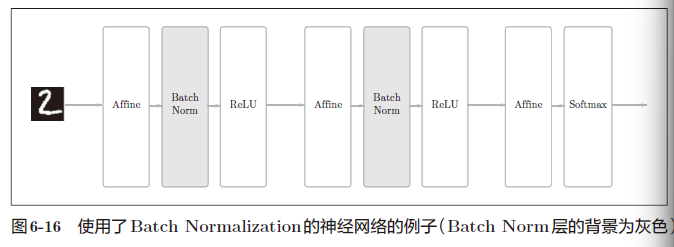
Batch Norm，顾名思义，以进行学习时的mini-batch 为单位，按minibatch进行正规化。具体而言，就是进行使数据分布的均值为0、方差为1 的正规化。用数学式表示的话，如下所示：

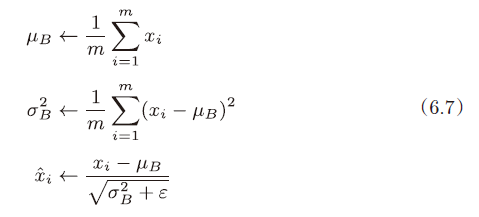
式（6.7）所做的是将mini-batch 的输入数据{x1, x2, . . . , xm} 变换为均值为0、方差为1 的数据，非常简单

通过将这个处理插入到激活函数的前面（或者后面），可以减小数据分布的偏向。

接着，Batch Norm层会对正规化后的数据进行缩放和平移的变换，用数学式可以如下表示。

γ 和β 是参数。一开始γ = 1，β = 0，然后再通过学习调整到合适的值。

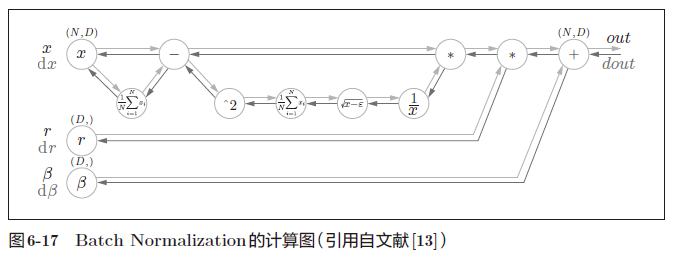
Batch Norm的反向传播的推导有些复杂，这里我们不进行介绍

Frederik Kratzert 的博客“Understanding the backward pass through Batch ormalization Layer”里有详细说明，感兴趣的读者可以参考一下。

Batch Normalization的评估

使用MNIST数据集，观察使用Batch Norm层和不使用Batch Norm层时学习的过程会如何变化（源代码在ch06/batch_norm_test.py中），结果如图6-18 所示

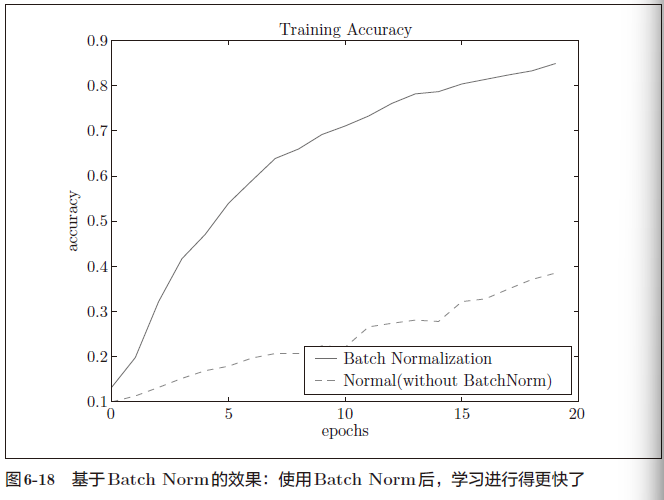
图6-19 是权重初始值的标准差为各种不同的值时的学习过程图。

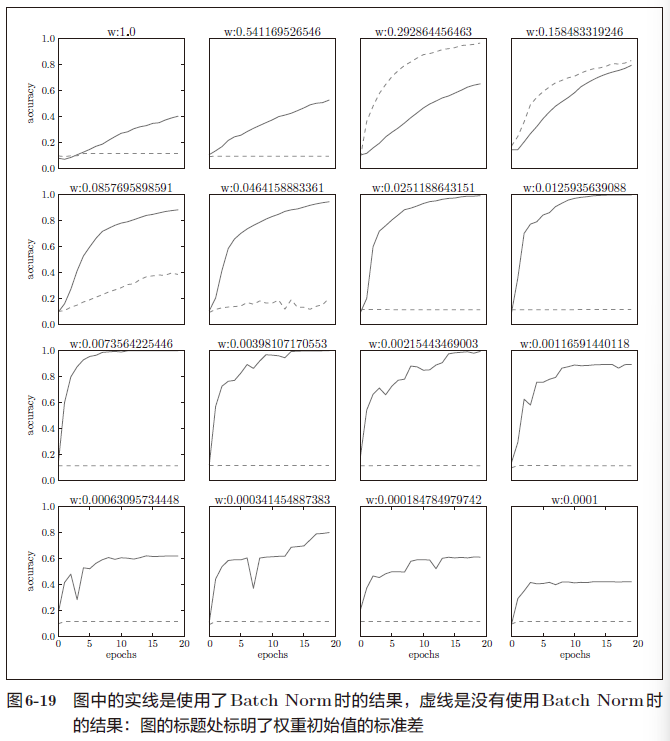
几乎所有的情况下都是使用Batch Norm时学习进行得更快

实际上，在不使用Batch Norm的情况下，如果不赋予一个尺度好的初始值，学习将完全无法进行。

综上，通过使用Batch Norm，可以推动学习的进行。并且，对权重初始值变得健壮（“对初始值健壮”表示不那么依赖初始值）。Batch Norm具备了如此优良的性质，一定能应用在更多场合中。

正则化

机器学习的问题中，过拟合是一个很常见的问题

机器学习的目标是提高泛化能力，即便是没有包含在训练数据里的未观测数据，也希望模型可以进行正确的识别

过拟合

发生过拟合的原因，主要有以下两个。

• 模型拥有大量参数、表现力强。
• 训练数据少。

首先是用于读入数据的代码。

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 为了再现过拟合，减少学习数据
x_train = x_train[:300]
t_train = t_train[:300]

接着是进行训练的代码

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100,100, 100, 100], output_size=10)
optimizer = SGD(lr=0.01) # 用学习率为0.01的SGD更新参数

max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0

for i in range(1000000000):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    grads = network.gradient(x_batch, t_batch)
    optimizer.update(network.params, grads)
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        
        epoch_cnt += 1
        if epoch_cnt >= max_epochs:
            break

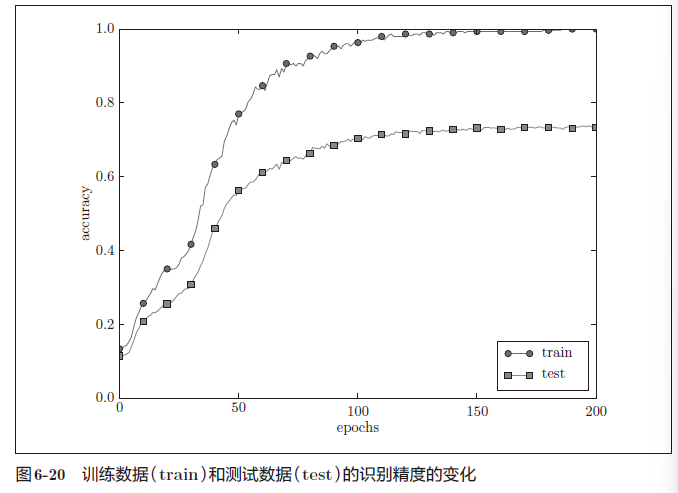
从图中可知，模型对训练时没有使用的一般数据（测试数据）拟合得不是很好。

权值衰减

权值衰减是一直以来经常被使用的一种抑制过拟合的方法

该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。很多过拟合原本就是因为权重参数取值过大才发生的。

神经网络的学习目的是减小损失函数的值，例如为损失函数加上权重的平方范数（L2 范数）。这样一来，就可以抑制权重变大。
$$用符号表示的话，如果将权重记为W，L2范数的权值衰减就是\frac{1}{2}\lambda W^2，然后将这个\frac{1}{2}\lambda W^2加到损失函数上$$
λ是控制正则化强度的超参数。λ设置得越大，对大的权重施加的惩罚就越重
$$此外，\frac{1}{2}\lambda W^2开头的是用于将的求导结果变成\lambda W的调整用常量$$
​

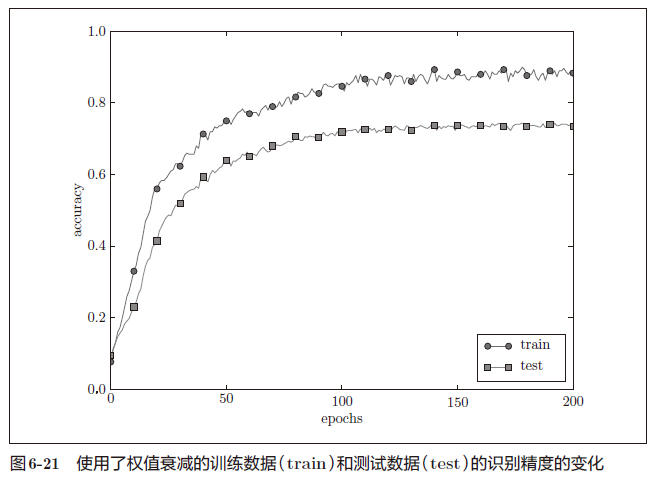
如图6-21 所示，虽然训练数据的识别精度和测试数据的识别精度之间有差距，但是与没有使用权值衰减的图6-20 的结果相比，差距变小了。这说明过拟合受到了抑制。此外，还要注意，训练数据的识别精度没有达到100%（1.0）

Dropout

如果网络的模型变得很复杂，只用权值衰减就难以应对了。在这种情况下，我们经常会使用Dropout 方法。

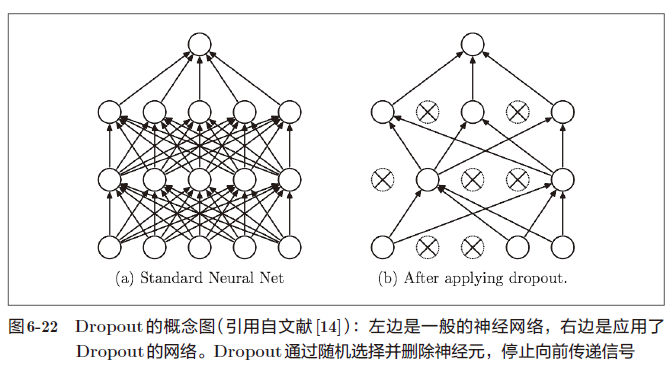
Dropout 是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递，如图6-22 所示

训练时，每传递一次数据，就会随机选择要删除的神经元。

测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出

class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None
    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)
    def backward(self, dout):
        return dout * self.mask

正向传播时传递了信号的神经元，反向传播时按原样传递信号；正向传播时没有传递信号的神经元，反向传播时信号将停在那里。

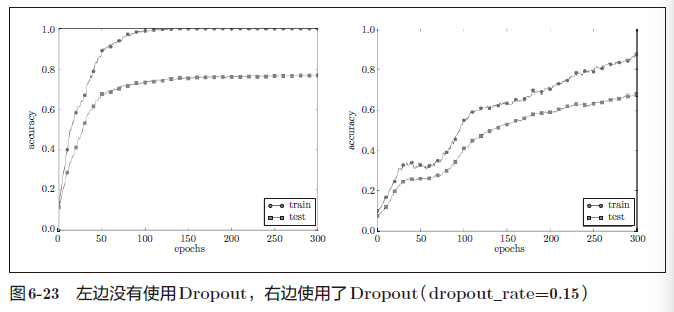
像这样，通过使用Dropout，即便是表现力强的网络，也可以抑制过拟合。

[!IMPORTANT]

机器学习中经常使用集成学习。所谓集成学习，就是让多个模型单独进行学习，推理时再取多个模型的输出的平均值

Dropout将集成学习的效果（模拟地）通过一个网络实现了。

超参数的验证

神经网络中，除了权重和偏置等参数，超参数（hyper-parameter）也经常出现。

虽然超参数的取值非常重要，但是在决定超参数的过程中一般会伴随很多的试错。本节将介绍尽可能高效地寻找超参数的值的方法。

验证数据

不能使用测试数据评估超参数的性能。这一点非常重要，但也容易被忽视。

为什么不能用测试数据评估超参数的性能呢？

用测试数据确认超参数的值的“好坏”，就会导致超参数的值被调整为只拟合测试数据。这样的话，可能就会得到不能拟合其他数据、泛化能力低的模型。

调整超参数时，必须使用超参数专用的确认数据。用于调整超参数的数据，一般称为验证数据（validation data）

[!IMPORTANT]

训练数据用于参数（权重和偏置）的学习，验证数据用于超参数的性能评估。为了确认泛化能力，要在最后使用（比较理想的是只用一次）测试数据。

如果是MNIST数据集，获得验证数据的最简单的方法就是从训练数据中事先分割20%作为验证数据

(x_train, t_train), (x_test, t_test) = load_mnist()
# 打乱训练数据
x_train, t_train = shuffle_dataset(x_train, t_train)
# 分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]

因为数据集的数据可能存在偏向（比如，数据从“0”到“10”按顺序排列等）。这里使用的shuffle_dataset函数利用了np.random.shuffle，在common/util.py中有它的实现。

超参数的最优化

进行超参数的最优化时，逐渐缩小超参数的“好值”的存在范围非常重要。

所谓逐渐缩小范围，是指一开始先大致设定一个范围，从这个范围中随机选出一个超参数（采样），用这个采样到的值进行识别精度的评估；然后，多次重复该操作，观察识别精度的结果，根据这个结果缩小超参数的“好值”的范围。通过重复这一操作，就可以逐渐确定超参数的合适范围。

• 步骤0
  • 设定超参数的范围（用对数尺度指定）
• 步骤1
  • 从设定的超参数范围中随机采样
• 步骤2
  • 使用步骤1中采样到的超参数的值进行学习，通过验证数据评估识别精度（但是要将epoch设置得很小）
• 步骤3
  • 重复步骤1和步骤2（100次等），根据它们的识别精度的结果，缩小超参数的范围

[!IMPORTANT]

这里介绍的超参数的最优化方法是实践性的方法。不过，这个方法与其说是科学方法，倒不如说有些实践者的经验的感觉。在超参数的最优化中，如果需要更精炼的方法，可以使用贝叶斯最优化（Bayesian optimization）。贝叶斯最优化运用以贝叶斯定理为中心的数学理论，能够更加严密、高效地进行最优化。详细内容请参考论文“Practical Bayesian Optimization of Machine Learning Algorithms”等。

超参数最优化的实现

现在，我们使用MNIST数据集进行超参数的最优化。这里我们将学习率和控制权值衰减强度的系数（下文称为“权值衰减系数”）这两个超参数的搜索问题作为对象

如前所述，通过从0.001（10^{−3）到1000（10}3）这样的对数尺度的范围中随机采样进行超参数的验证.这在Python 中可以写成10 ** np.random.uniform(-3, 3)

在该实验中，权值衰减系数的初始范围为10−8 到10−4，学习率的初始范围为10−6 到10−2。此时，超参数的随机采样的代码如下所示。

weight_decay = 10 ** np.random.uniform(-8, -4) lr = 10 ** np.random.uniform(-6, -2)

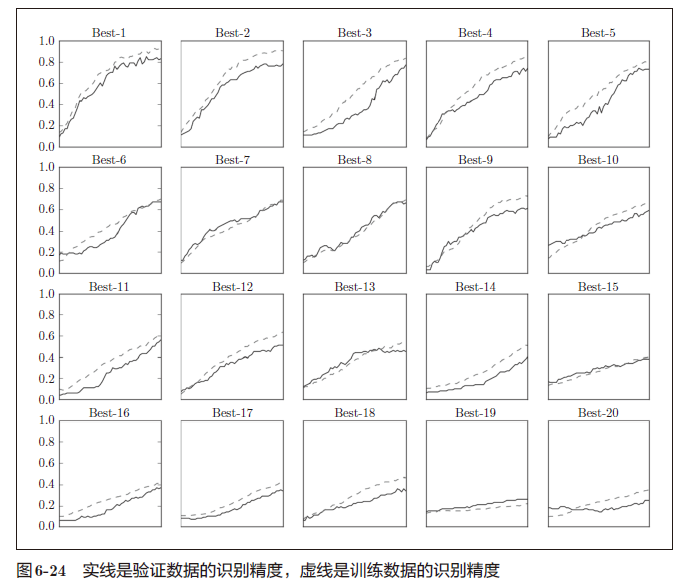
像这样进行随机采样后，再使用那些值进行学习。之后，多次使用各种超参数的值重复进行学习，观察合乎逻辑的超参数在哪里

小结

• 参数的更新方法，除了SGD 之外，还有Momentum、AdaGrad、Adam等方法。
• 权重初始值的赋值方法对进行正确的学习非常重要。
• 作为权重初始值，Xavier 初始值、He初始值等比较有效。
• 通过使用Batch Normalization，可以加速学习，并且对初始值变得健壮。
• 抑制过拟合的正则化技术有权值衰减、Dropout等。
• 逐渐缩小“好值”存在的范围是搜索超参数的一个有效方法。