最大上升子序列问题也叫做LIS问题，与最大公共子序列LCS问题是一类经典问题，在本章我们将总结一下求解LIS最大上升子序列的几种方法，同时也会给出对应的最大不上升子序列的求解方法。 关于LCS问题，我在后面会再出一篇博客来讲解，

废话不多说，我们直接进入正题，如果你还一点都不了解LIS问题，那么请不要看这篇博客，本篇博客只是对于LIS的求解的总结与归纳，但凡是涉及结论公式求证的我一概不会论证，其实是我不会 ，在这里我将会直接使用

---

最大上升子序列： [4,2,3,6,9] 是一个序列，那么显而易见他的LIS应该是 [2,3,6,9]，长度为4吗，注意LIS问题是可以不连续的，我这个例子是连续的。

动态规划

我们定义dp[i] 作为以i结尾的子序列的最大上升子序列的长度

因此，我们可以知道，如果我们要求dp[i]，必须首先对i之前位置的元素 j 进行逐一遍历，然后和i位置的元素比较，只要j位置的元素小于i位置的元素，那么就是一个满足条件的元素，注意整个过程中需要满足
$$j<i，a[j]<a[i]$$
那么我们便可以通过来求得dp[i]
$$dp[i]=max(dp[i],dp[j]+1)$$
因为如果找到了一个符合条件的 a[j]<a[i] ，那么j这个位置的元素就可以是dp[i]的一个最大上升子序列的元素，因此dp[j]+1 将此长度加1，由于dp是一个状态转移的过程，我们还要确保之前的值与当前求得最长的长度要取得一个最大值

代码如下：

/*
	最长上升子序列
	*/
	for (int i = 1; i <= n; i++)
	{	
		dpAdd[i] = 1;	//以每一个i位置开始的元素的默认最长上升子序列长度是1(该元素本身)
		for (int j = 1; j < i; j++)	//遍历所有比i位置小的元素
		{
			if (a[j] < a[i])	//查找前面的位置的元素是否小于i位置
			{
				//存在一个比i位置小的元素在j位置，则记录j位置dp要加1，表示在j位置的后面可以找到一个i位置，使得i位置的元素比j位置大，i和j满足一个上升的子序列，所以取dp[j]+1 和 它本身的dp[i]的较大者
				dpAdd[i] = max(dpAdd[i], dpAdd[j] + 1);
			}
		}
		//dp[i]更新为[0,i]区间内的最长上升子序列的最大长度
		res = max(res, dpAdd[i]);
	}

---

求解最大不上升子序列的问题也是如此：
最大不上升子序列指的是当前元素的后面的所有元素都小于等于当前元素，即
$$i<j，a[i]>=a[j]$$
它的dp状态转移方程是一样的，因此我们便可以通过将遍历顺序倒过来，来求解最大不上升子序列问题。

/*
	最长不上升子序列
	*/
	for (int i = n; i >= 1; i--)
	{
		dpNAdd[i] = 1;
		for (int j = i + 1; j <= n; j++)	//在i的后面的元素开始
		{
			if (b[j] <= b[i])	//i后面的要小于等于i，所以才是不上升的
			{
				dpNAdd[i] = max(dpNAdd[i], dpNAdd[j] + 1);
			}
		}
		ans = max(ans, dpNAdd[i]);
	}

---

可见，在用DP方法来求解LIS问题中，我们用到了两重循环，因此在最差的情况下我们的时间复杂度为$$O(N^2)$$

另外我们可以发现，我们在DP的过程中，注意到在转移的过程中，我们需要反复地从 i - i中找满足条件的 j的位置，并且寻找最大的 a[j]，那么我们可以把这个过程抽象为一个从区间中寻找最大值的过程，那么我们便可以使用树状数组或者线段树来对这个过程进行维护。

---

树状数组

我们使用树状数组来查询 1-i 中的区间的最大值，这里我简单画了一个树状数组的实现的过程：

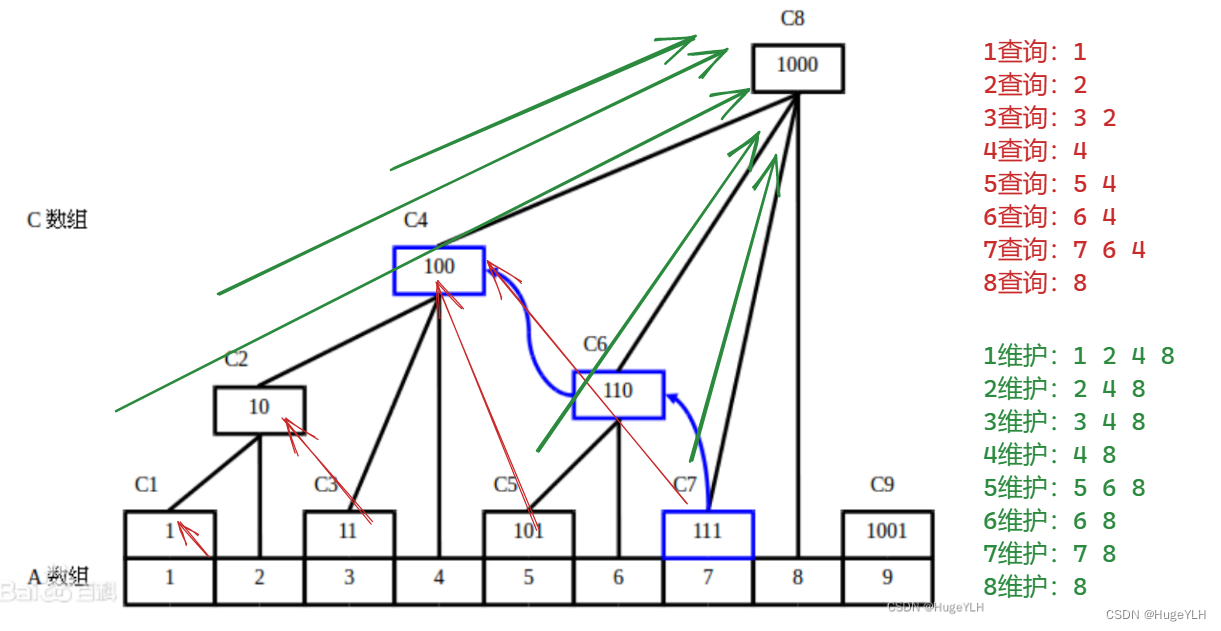
需要注意的点：

1. 在查询最大上升子序列的时候，由于前面的元素j不能等于 i位置，所以我们干脆就查询 a[i]-1,这样就做到了在 i之前查询
2. 在查询最大不上升子序列的时候，我们就把遍历的顺序从后往前，这样就做到了查询了i之后的元素，同时是小于等于的，直接a[i]即可。
3. 每次查询的时候都需要最后加上1，因为还要包含其自身

为什么可以使用树状数组？

我认为如上图所示，树状数组每次查询的时候都是查询所有比它小的位置的元素，而这些位置对于i来说都是 j<i 的，所以说只要在查询的时候获得一个最大值，即获得了以i结尾的最大不上升子序列的长度。

代码如下：

int tree[N];		
inline int lowbit(int i)
{
	return i & (-i);
}
void update(int i,int val)
{
	while (i <= maxn)
	{
		tree[i] = max(tree[i], val);
		i += lowbit(i);
	}
}
int query(int i)
{
	int sum = 0;
	while (i > 0)
	{
		sum = max(sum, tree[i]);
		i -= lowbit(i);
	}
	return sum;
}

int main()
{
	/*
	最长上升子序列
	*/
	maxn = 9;	//数组的元素最大值
	for (int i = 1; i <= n; i++)
	{
		int num = query(a[i] - 1) + 1;
		/*
		相当于for (int j=1;j<i;j++) if (a[j]<a[i])
			查询以a[i]结尾的最长上升子序列的最大长度，注意：查询时不包含a[i]元素，所以长度要再加1
		*/
		update(a[i], num);//维护树状数组，即维护了各个位置元素的最大上升子序列的长度
		res = max(res, num);
	}
	cout << res << endl << endl;

	memset(tree, 0, sizeof(tree));
	/*
	最长不上升子序列
	*/
	for (int i = n; i >= 1; i--)
	{
		//要查询的是不上升，所以后面的小于等于前面的，所以说查询时包括b[i]，无须向上面一样减1
		int num = query(b[i]) + 1;	

		update(b[i], num);
		ans = max(ans, num);
	}
	cout << ans;
	return 0;
}

---

树状数组的查询是$$O(NlogN)$$

---

线段树

线段树和树状数组的解法相同，只不过线段树代码量多，但是线段树易懂，树状数组比较抽象

代码如下：

/*
线段树
*/
int add[N];

inline void push_up(int i)
{
	//上移，维护区间最大值
	tree[i] = max(tree[i << 1], tree[i << 1 | 1]);
}
void build(int i, int pl, int pr)
{
	if (pl == pr)
	{
		tree[i] = 0;
		return;
	}
	int mid = (pl + pr) >> 1;
	build(i << 1, pl, mid);
	build(i << 1 | 1, mid + 1, pr);
	push_up(i);
}
void update(int i, int pl, int pr, int x, int val)
{
	if (pl == pr)
	{
		tree[i] = max(tree[i], val);
		return;
	}
	int mid = (pl + pr) >> 1;
	if (x <= mid) update(i << 1, pl, mid, x,val);	//递归左子树
	if (x > mid) update(i << 1 | 1, mid + 1, pr, x, val);//递归右子树
	push_up(i);
}
int query(int i, int pl, int pr, int L, int R)
{
	if (L > R) return 0;
	if (L <= pl && pr <= R)
	{
		return tree[i];
	}
	int ans = 0;
	int mid = (pl + pr) >> 1;
	if (L <= mid) ans =max(ans,query(i << 1, pl, mid, L, R));
	if (R > mid) ans =max(ans, query(i << 1 | 1, mid + 1, pr, L, R));
	return ans;
}

int main3()
{
	build(1, 1, n);
	/*
	最大上升子序列
	*/
	for (int i = 1; i <= n; i++)
	{
		//查询以i结尾的最大上升子序列长度的最大值，是小于号，所以说要减1
		int num = query(1, 1, n, 1, a[i] - 1) + 1;	

		update(1, 1, n, a[i], num);
		res = max(res, num);
	}
	cout << res << endl << endl;
	return 0;
}

线段树的时间复杂度也是$$O(NlogN)$$

---

二分查找

关于二分查找的详细的解释：
二分查找的详细解释

• 最长上升子序列：

  • 如果最后一个元素小于下一个元素，则满足
  • 否则在升序序列中查找第一个大于等于x的元素，然后替换

• 最长不上升子序列

  • 如果最后一个元素大于等于下一个元素，则满足
  • 否则在降序序列中查找第一个大于x的元素，然后替换

/*
二分查找
*/

int d1[N], d2[N];
int main()
{
	int len1 = 1, len2 = 1;
	d1[1] = d2[1] = a[1];
	for (int i = 2; i <= n; i++)
	{
		//最长上升子序列，最后一个元素一定小于下一个元素
		if (d1[len1] < a[i]) d1[++len1] = a[i];
		else *lower_bound(d1 + 1, d1 + 1 + len1, a[i]) = a[i];
		//最长不上升子序列，最后一个元素一定大于等于下一个元素
		if (d2[len2] >= a[i]) d2[++len2] = a[i];
		else *upper_bound(d2 + 1, d2 + 1 + len2, a[i], greater<int>()) = a[i];
	}
	cout << len1 << " " << len2 << endl;

	return 0;
}

时间复杂度$$O（NlogN）$$