跳表(Skip List)是一种随机化的数据结构,用于替代平衡树(如 AVL 树或红黑树)。它是基于多层链表的,每一层都是上一层的子集。跳表可以提供与平衡树相似的搜索性能,即在最坏情况下,搜索、插入和删除操作都可以在 O(log n) 的时间复杂度内完成。
跳表的基本组成:
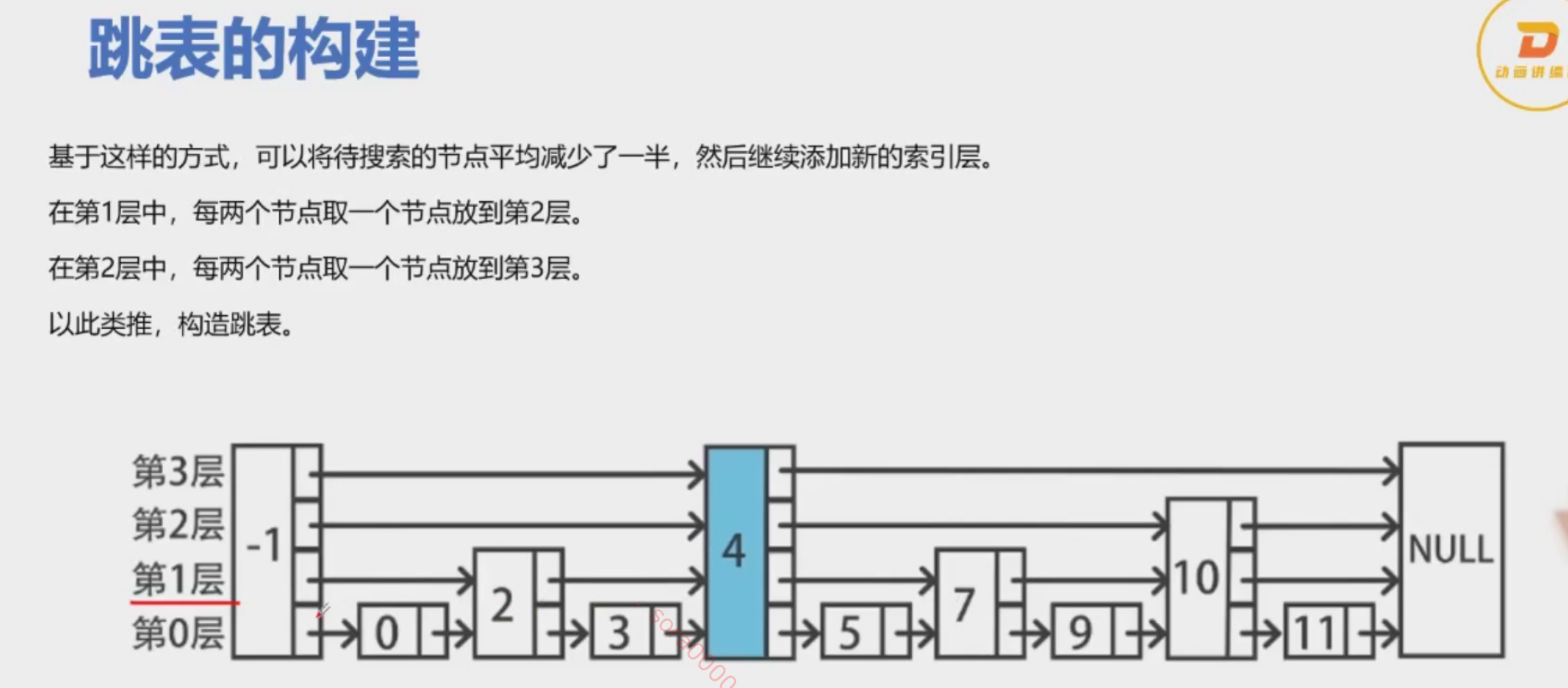
- 多层链表:跳表由若干层链表组成,每一层都是下面一层的“快速通道”。最底层是基础链表,包含所有的元素。
- 索引节点:每一层的链表都包含一些索引节点,这些节点指向下一层的某些节点。
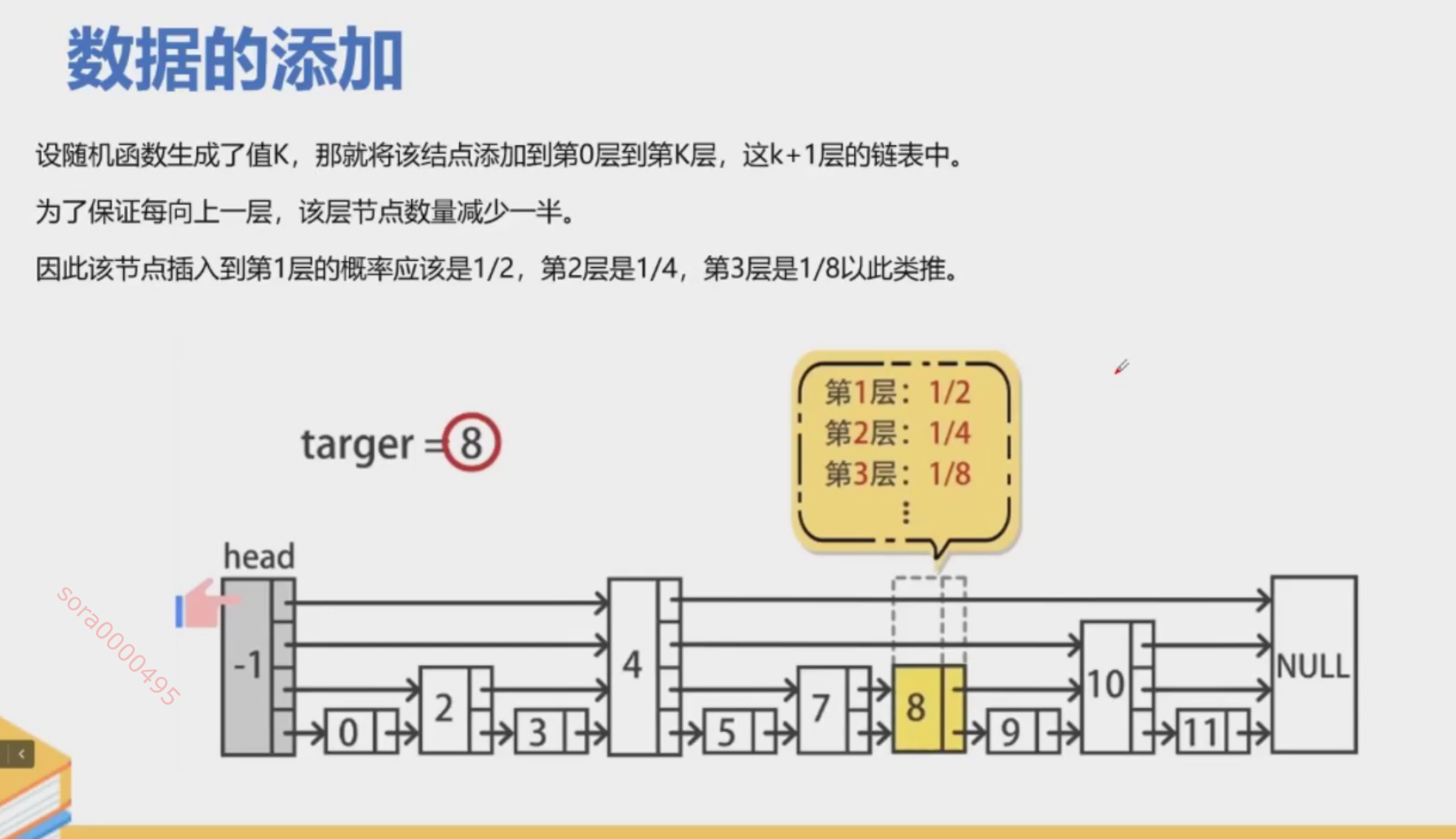
- 随机化:每个节点都有相同的概率(通常为 1/2)决定是否向上增加一层,从而创建一个索引节点。
跳表的操作:
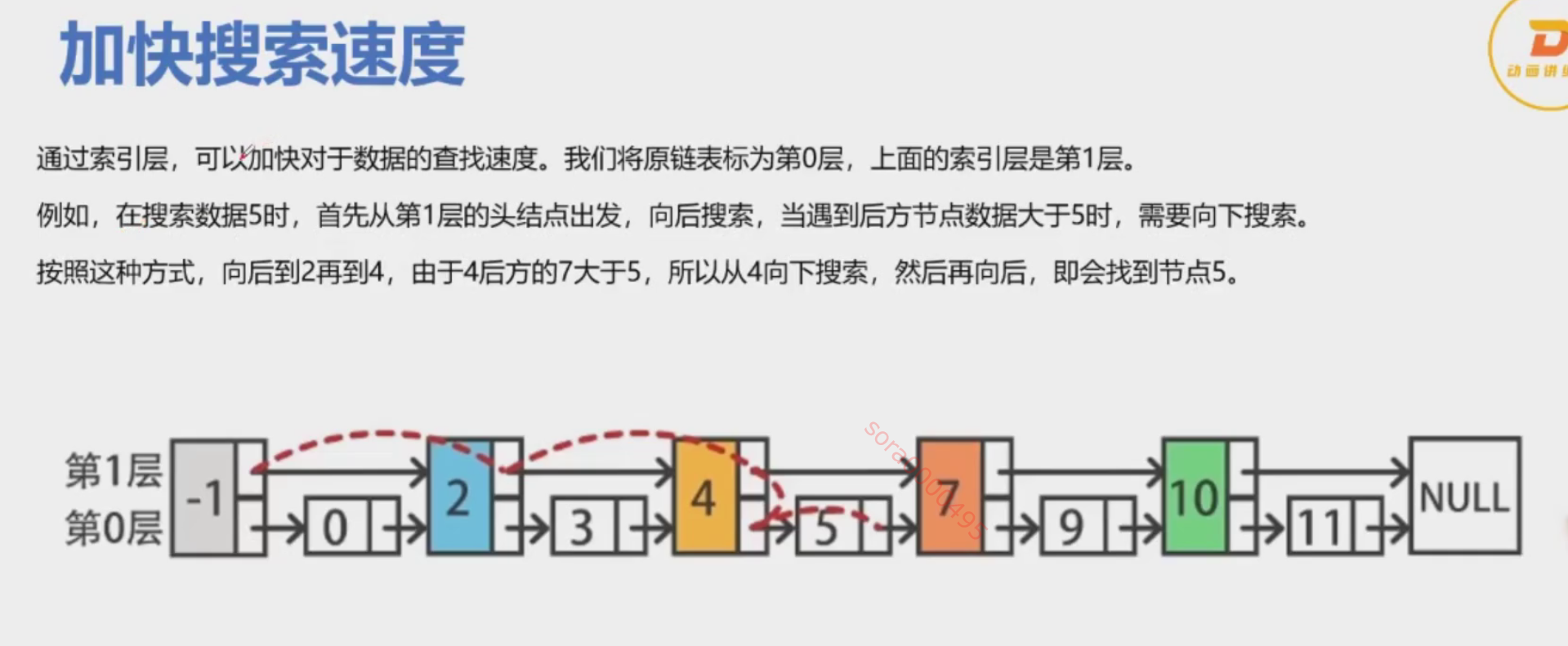
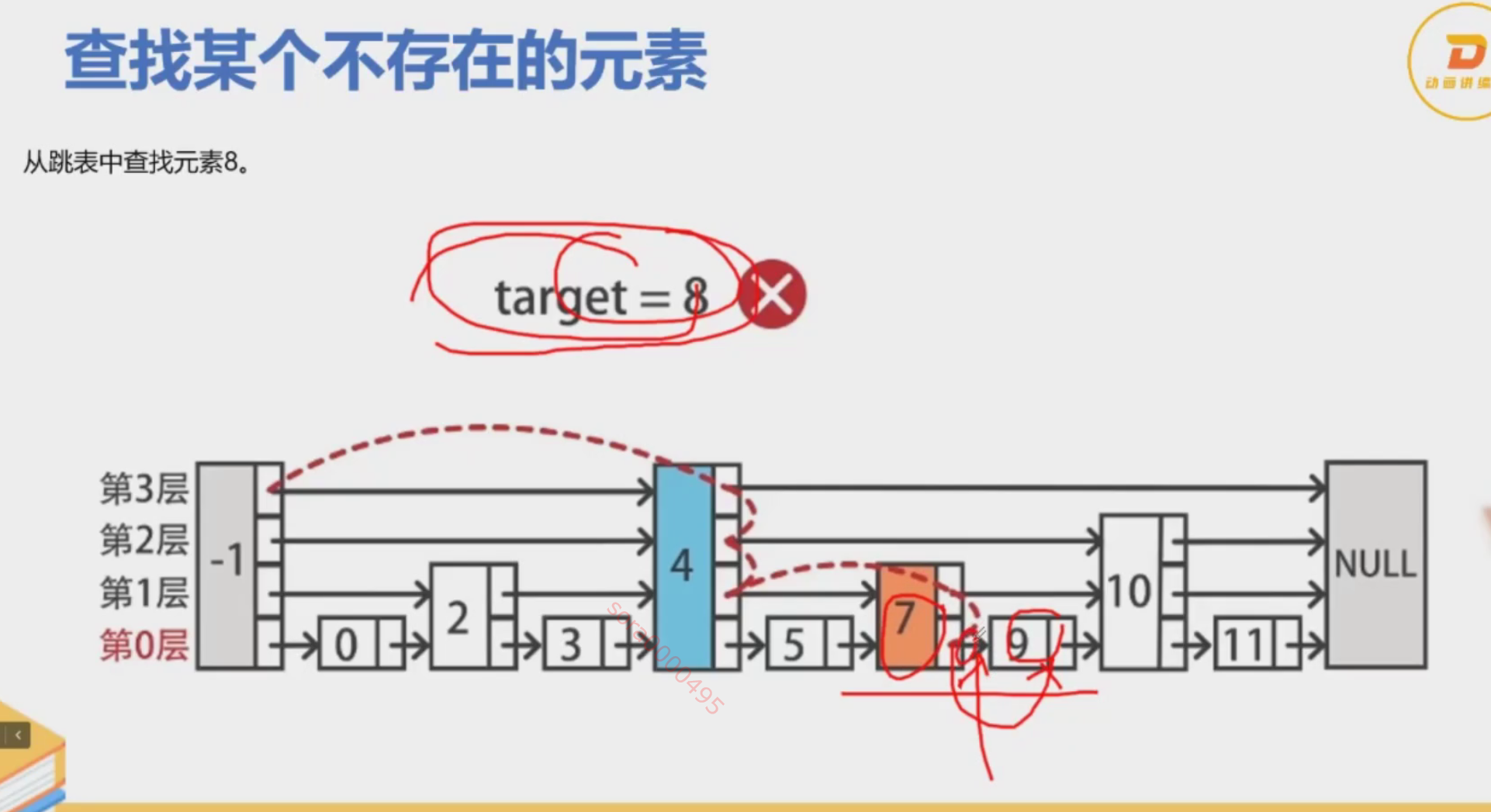
- 搜索:在跳表中搜索元素时,从顶层开始,逐层向下,直到找到元素或到达底层。在每一层,通过索引节点快速跳过多个节点。
- 插入:插入操作首先在底层进行标准的链表插入。然后,根据随机化过程决定是否在更高层创建索引节点。
- 删除:删除操作首先在所有包含该元素的层上找到它,然后逐层删除。如果某个层的索引节点在删除操作后变得无效(即前后节点相同),则该索引节点也会被删除。
跳表的优点:
- 简单性:跳表的实现相对简单,不需要复杂的旋转操作,如平衡树所需的。
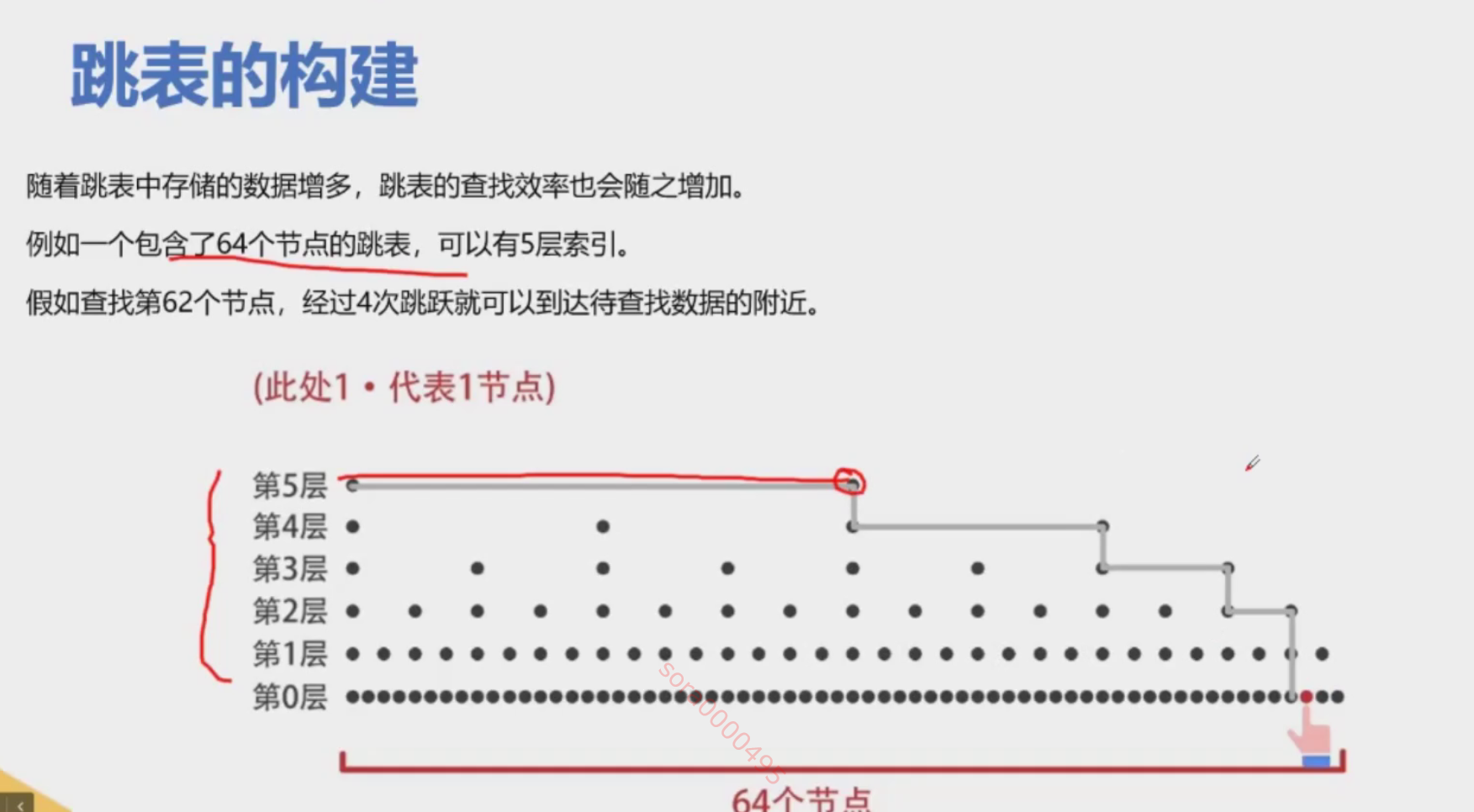
- 性能:跳表提供了与平衡树相似的搜索性能,且在某些情况下,由于其随机化的特性,可能具有更好的性能。
- 并发操作:跳表适合进行并发操作,因为它的插入和删除操作不需要像平衡树那样进行大量的结构调整。
跳表的应用:
跳表在许多场景下都有应用,尤其是在需要快速搜索、插入和删除操作的数据库和索引系统中。例如,Redis 这个流行的键值存储数据库就使用了跳表来实现有序集合。
跳表是一种非常实用的数据结构,它结合了链表的简单性和平衡树的高效搜索性能。
算法设计:
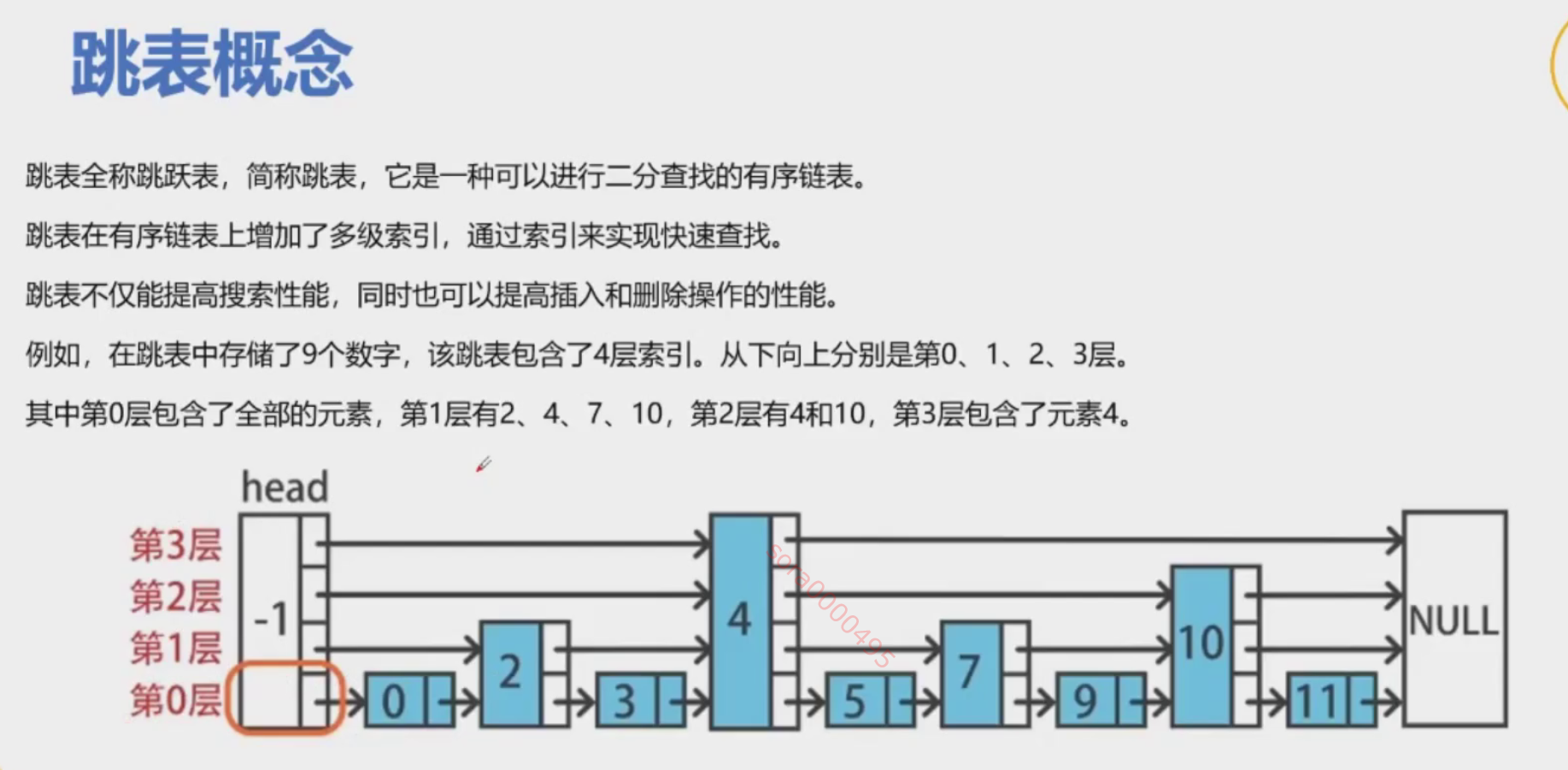
跳表的概念
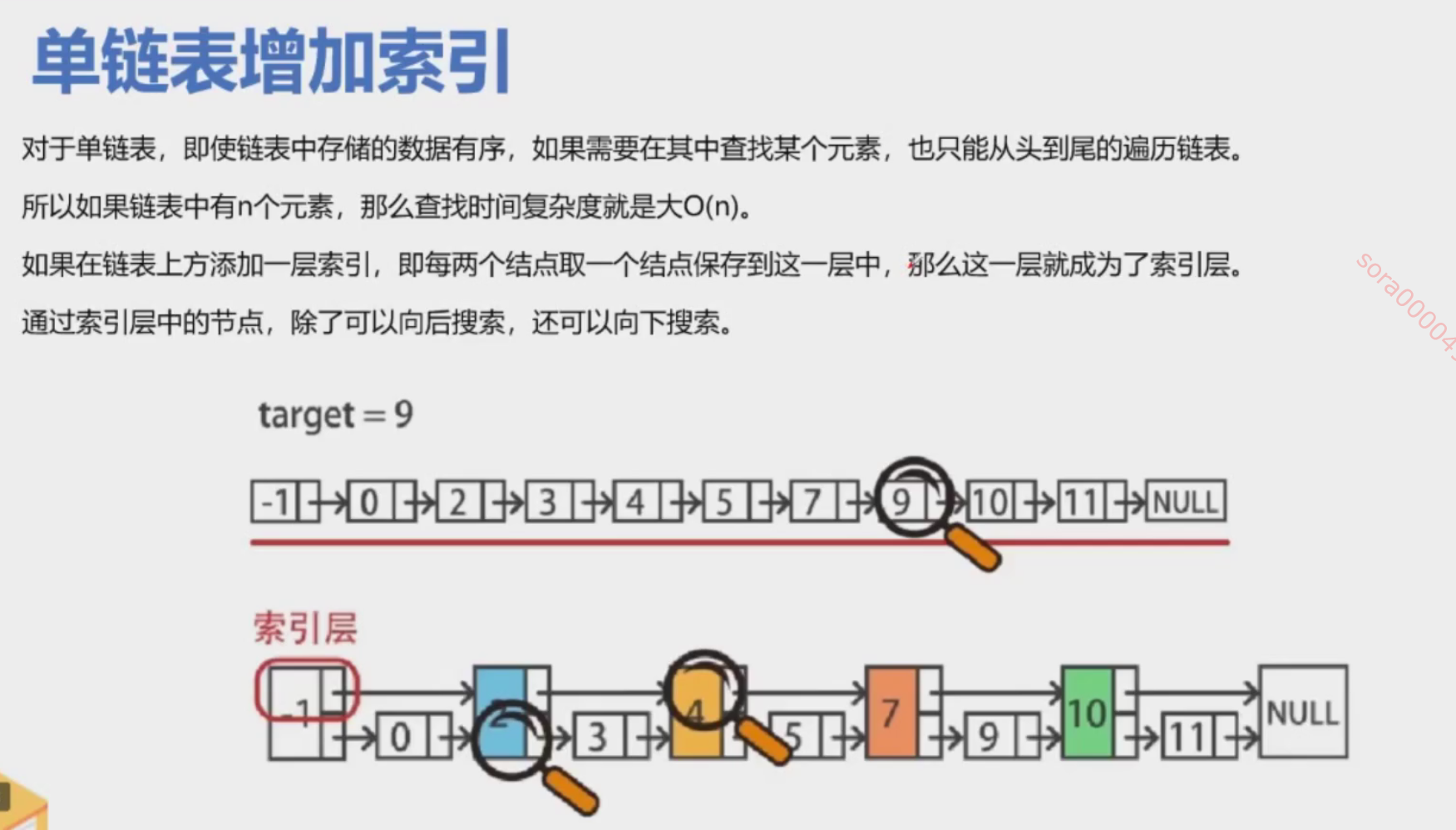
链表的优点
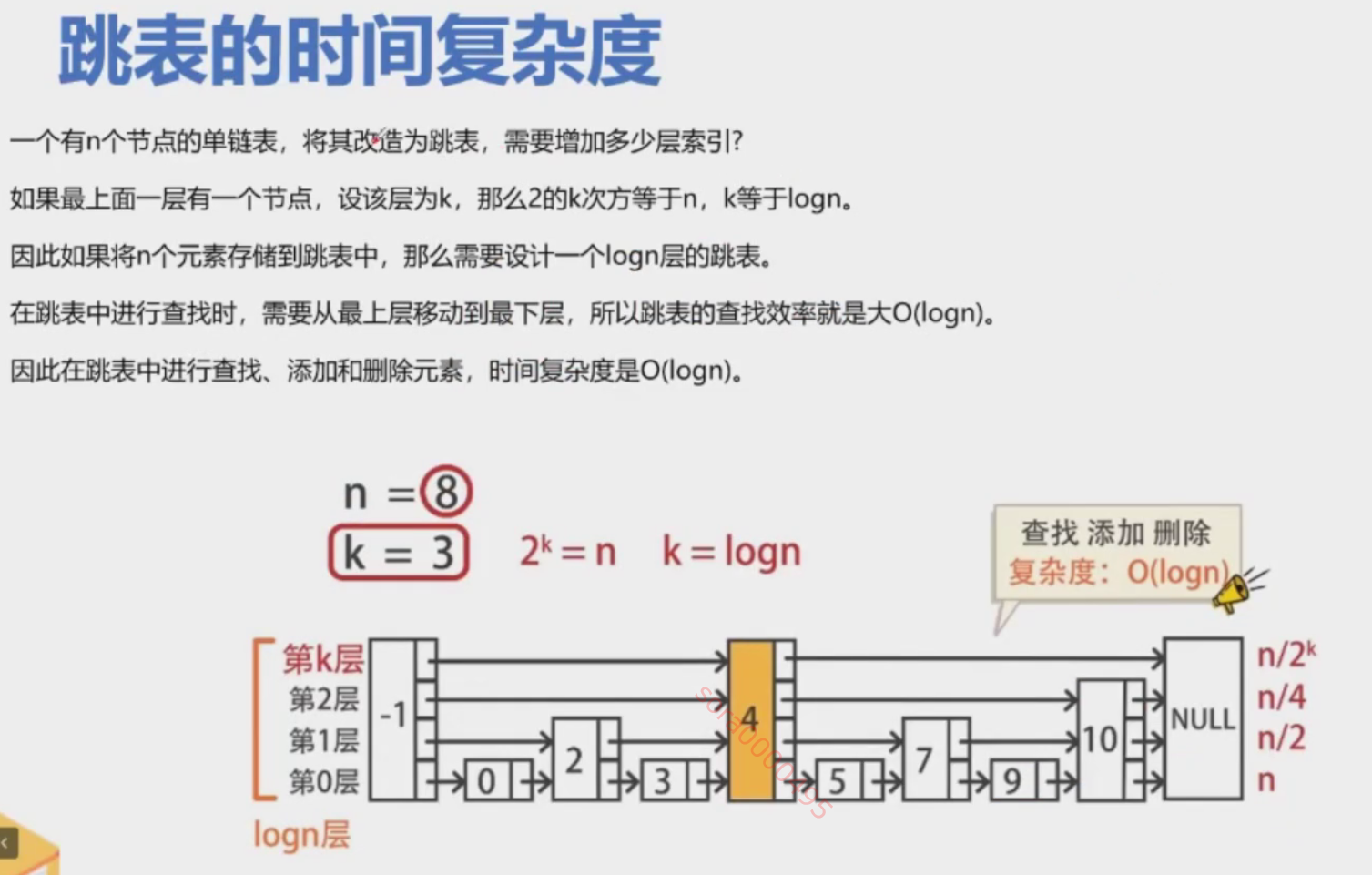
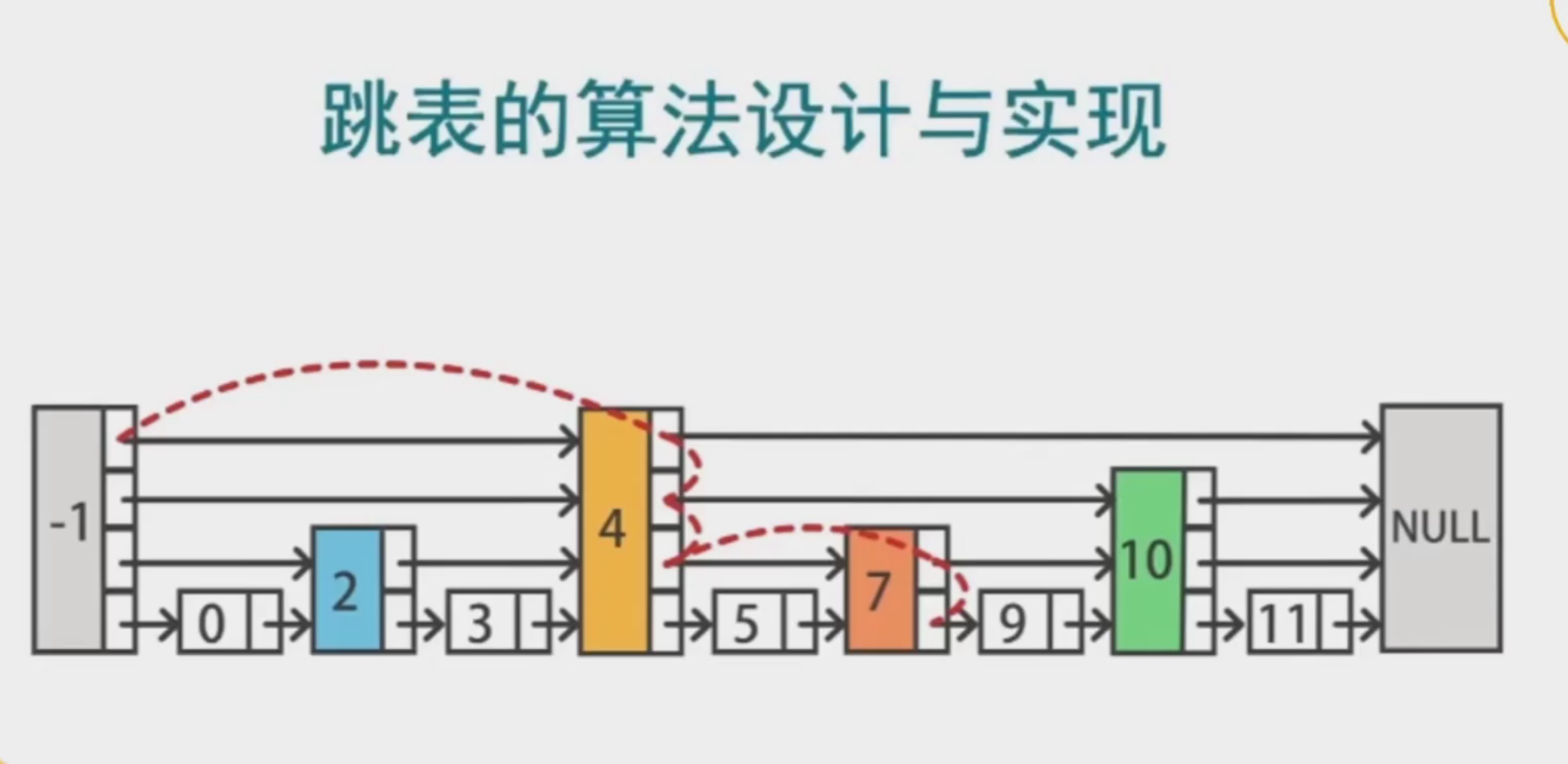
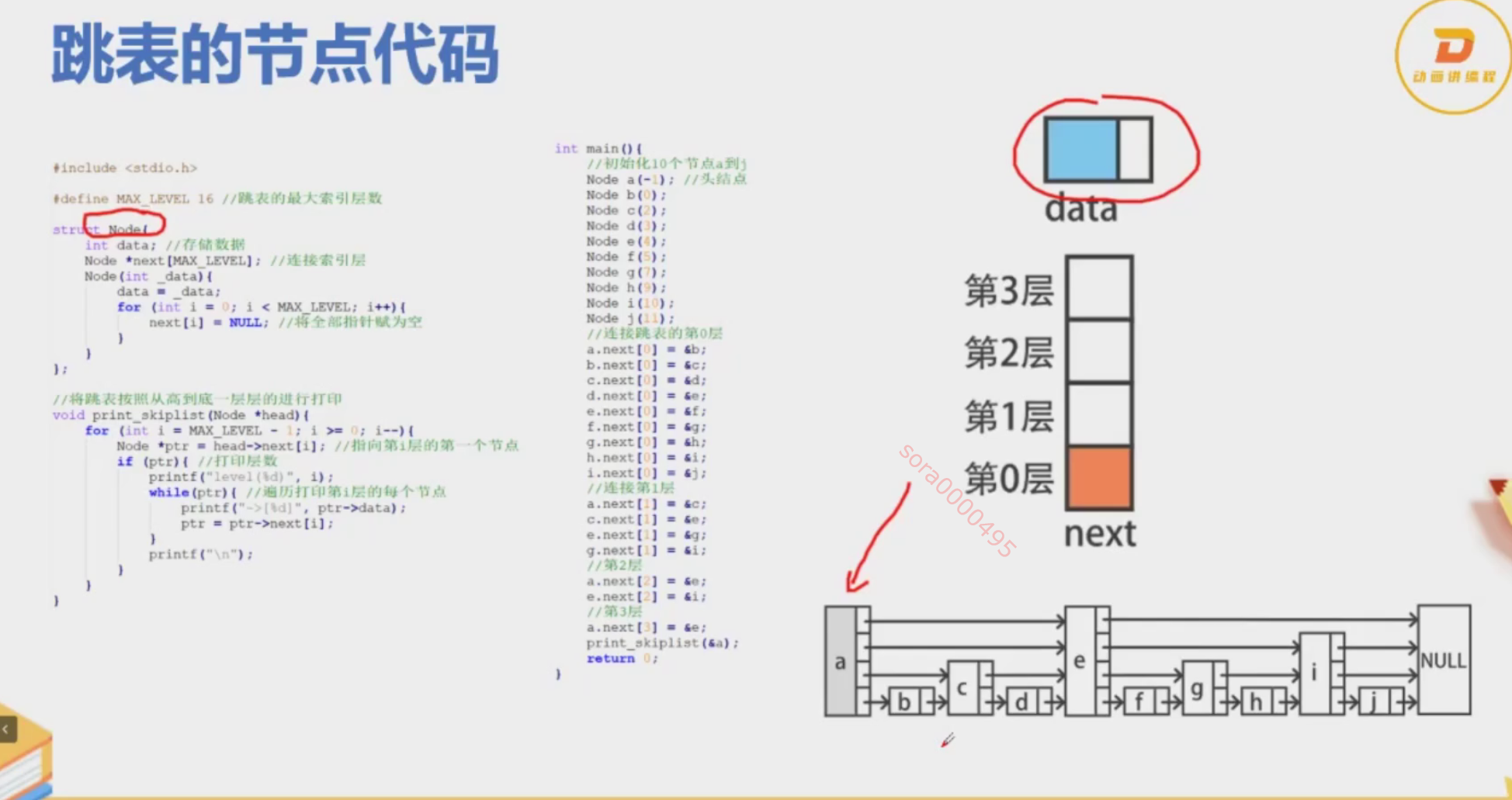
跳表的设计
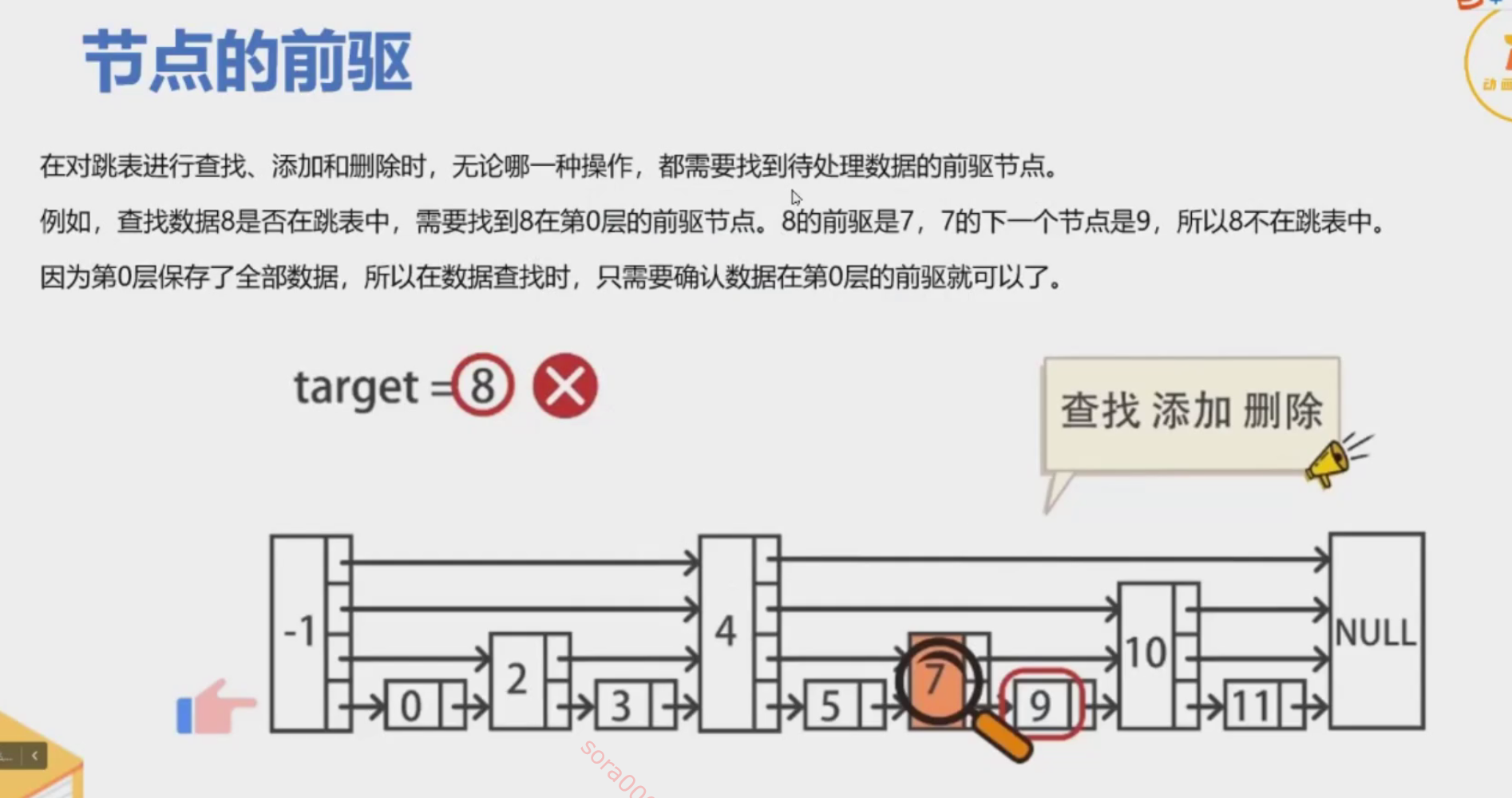
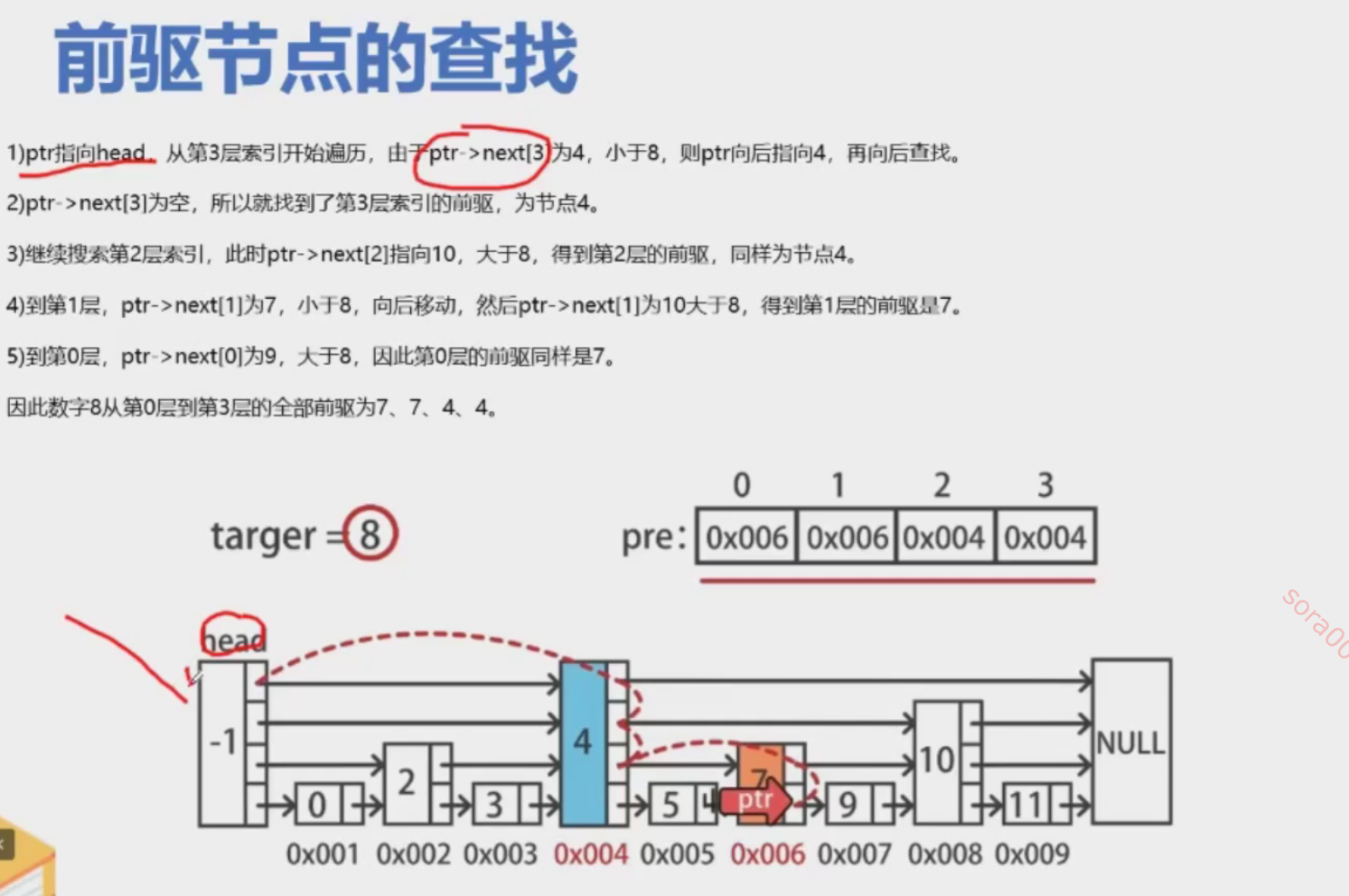
跳表中 的前驱
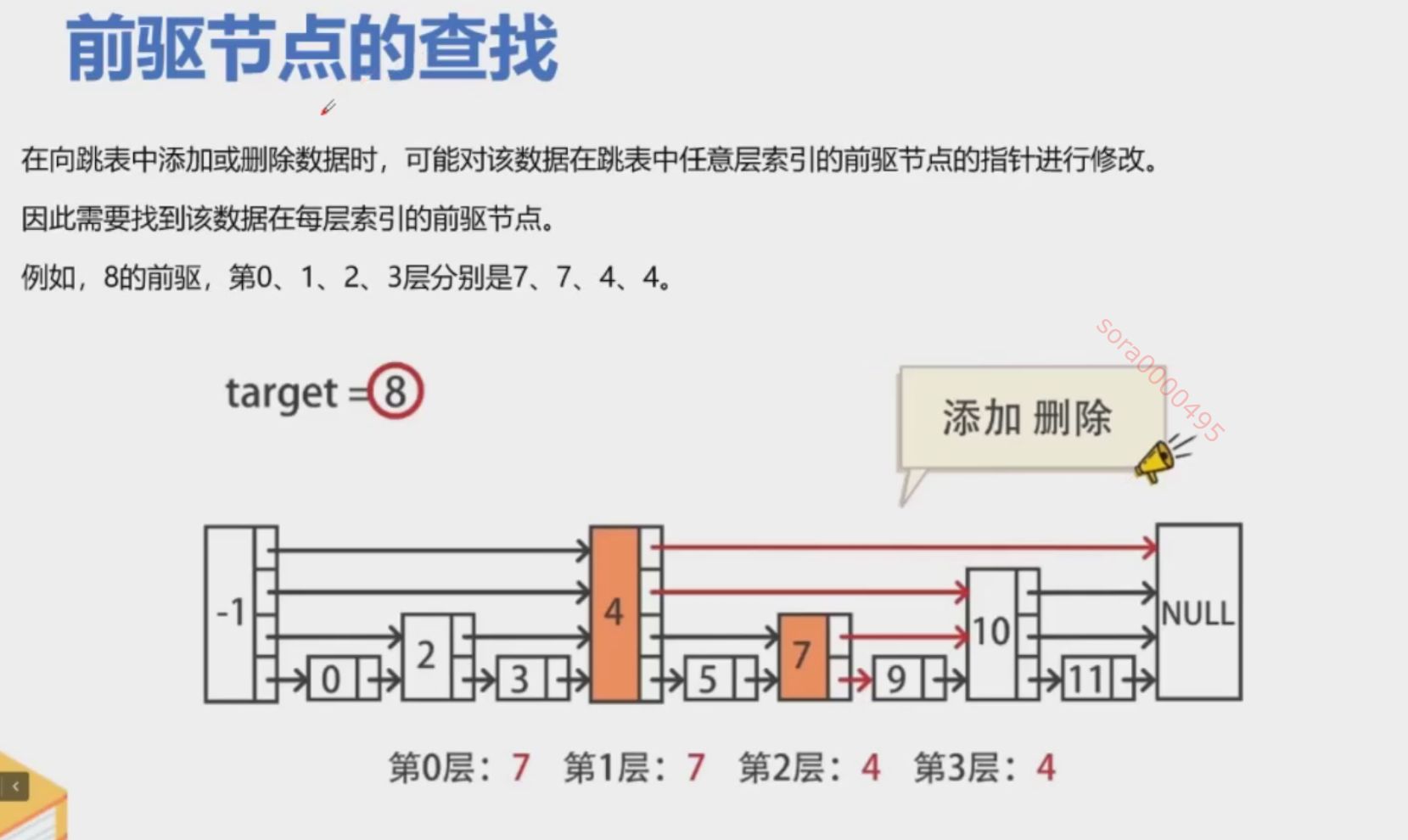

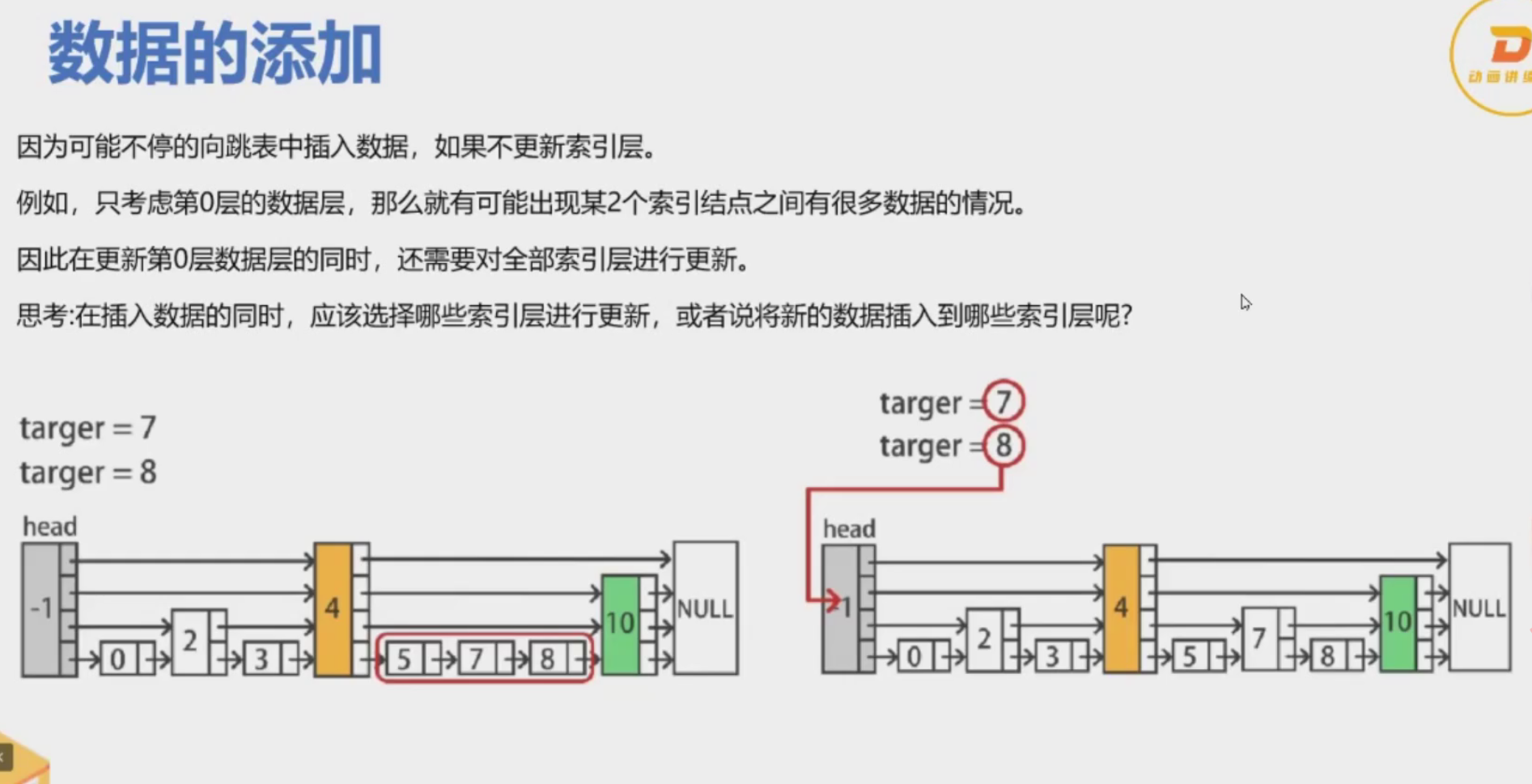
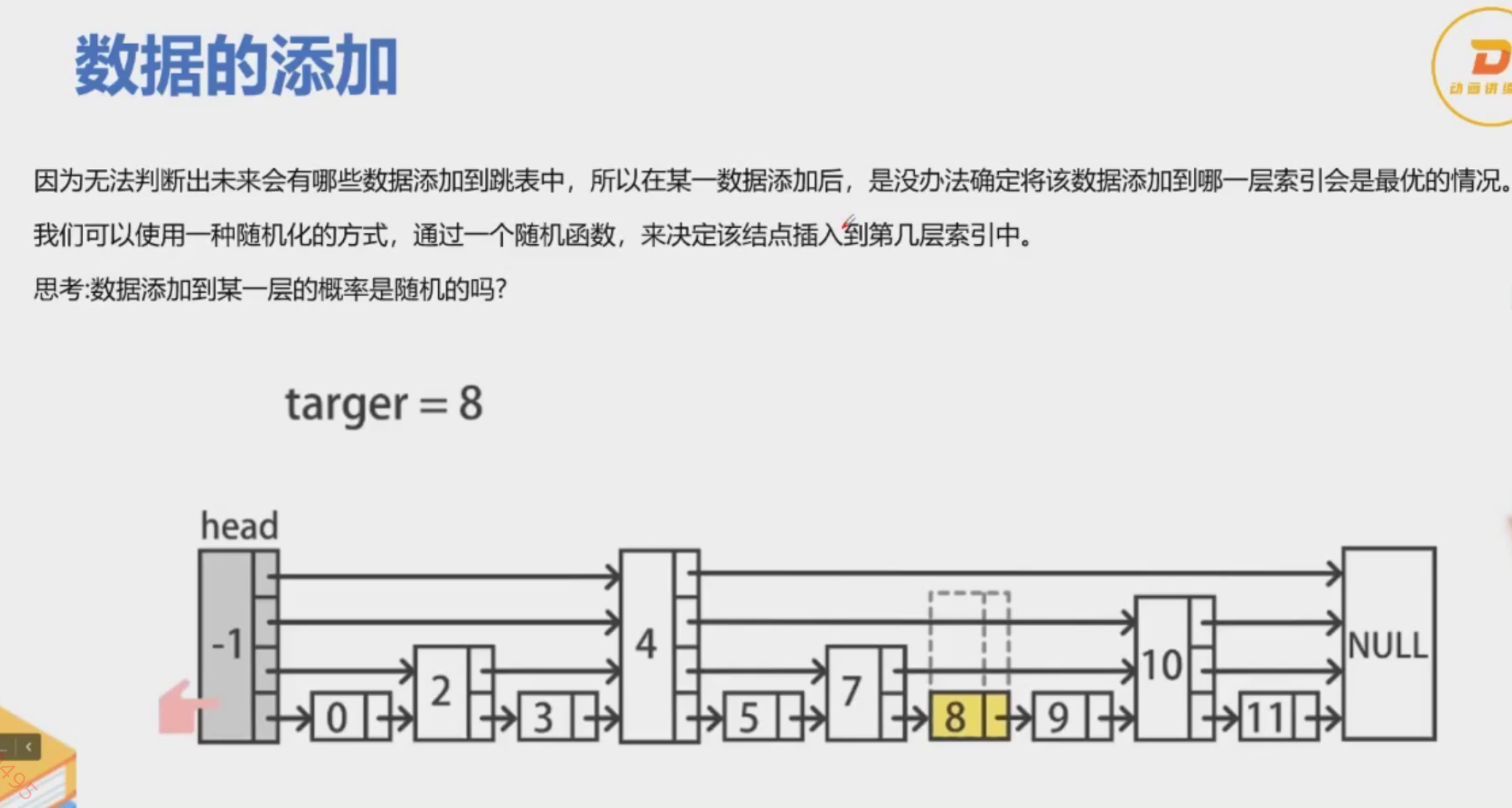
跳表的添加

跳表的删除


力扣1206 ---跳表
不使用任何库函数,设计一个 跳表 。
跳表 是在
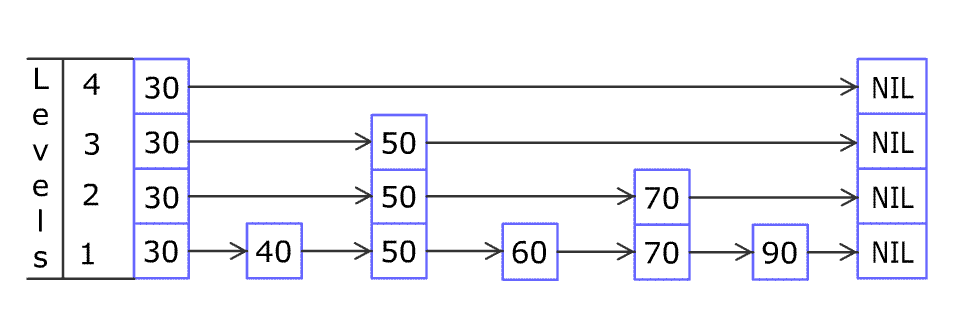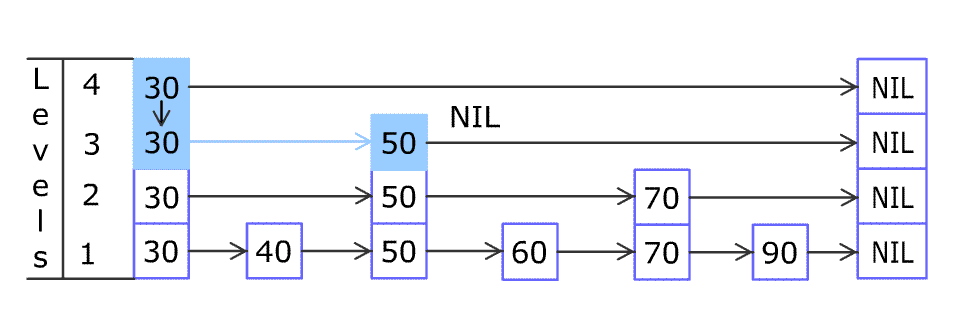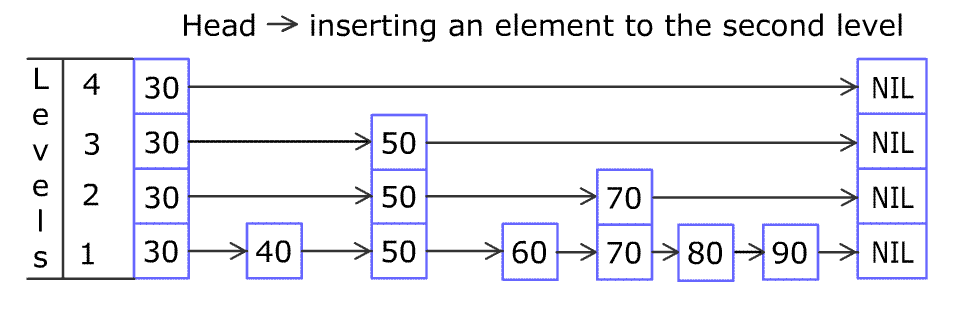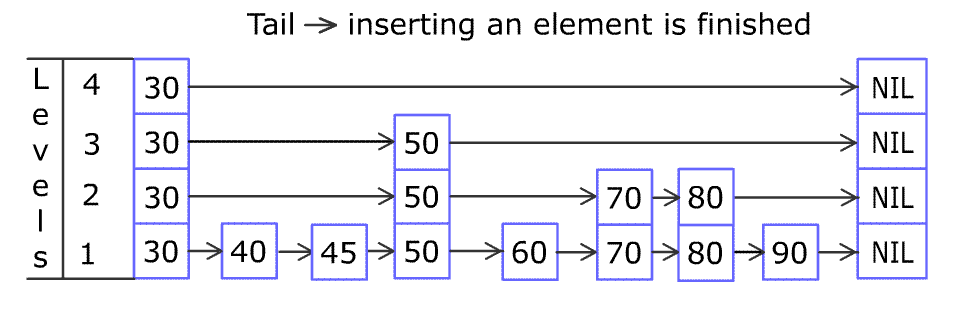
O(log(n))时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树,其功能与性能相当,并且跳表的代码长度相较下更短,其设计思想与链表相似。例如,一个跳表包含
[30, 40, 50, 60, 70, 90],然后增加80、45到跳表中,以下图的方式操作:
跳表中有很多层,每一层是一个短的链表。在第一层的作用下,增加、删除和搜索操作的时间复杂度不超过
O(n)。跳表的每一个操作的平均时间复杂度是O(log(n)),空间复杂度是O(n)。了解更多 : 跳表 - OI Wiki
在本题中,你的设计应该要包含这些函数:
bool search(int target): 返回target是否存在于跳表中。void add(int num): 插入一个元素到跳表。bool erase(int num): 在跳表中删除一个值,如果num不存在,直接返回false. 如果存在多个num,删除其中任意一个即可。注意,跳表中可能存在多个相同的值,你的代码需要处理这种情况。
示例 1:
输入 ["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"] [[], [1], [2], [3], [0], [4], [1], [0], [1], [1]] 输出 [null, null, null, null, false, null, true, false, true, false] 解释 Skiplist skiplist = new Skiplist(); skiplist.add(1); skiplist.add(2); skiplist.add(3); skiplist.search(0); // 返回 false skiplist.add(4); skiplist.search(1); // 返回 true skiplist.erase(0); // 返回 false,0 不在跳表中 skiplist.erase(1); // 返回 true skiplist.search(1); // 返回 false,1 已被擦除提示:
0 <= num, target <= 2 * 104- 调用
search,add,erase操作次数不大于5 * 104
代码
MAX_LEVEL = 32
P_FACTOR = 0.5
def random_level() -> int:
lv = 1
while lv < MAX_LEVEL and random.random() < P_FACTOR:
lv += 1
return lv
class SkiplistNode:
__slots__ = 'val', 'forward'
def __init__(self, val: int, max_level=MAX_LEVEL):
self.val = val
self.forward = [None] * max_level
class Skiplist:
def __init__(self):
self.head = SkiplistNode(-1)
self.level = 0
def search(self, target: int) -> bool:
curr = self.head
for i in range(self.level - 1, -1, -1):
# 找到第 i 层小于且最接近 target 的元素
while curr.forward[i] and curr.forward[i].val < target:
curr = curr.forward[i]
curr = curr.forward[0]
# 检测当前元素的值是否等于 target
return curr is not None and curr.val == target
def add(self, num: int) -> None:
update = [self.head] * MAX_LEVEL
curr = self.head
for i in range(self.level - 1, -1, -1):
# 找到第 i 层小于且最接近 num 的元素
while curr.forward[i] and curr.forward[i].val < num:
curr = curr.forward[i]
update[i] = curr
lv = random_level()
self.level = max(self.level, lv)
new_node = SkiplistNode(num, lv)
for i in range(lv):
# 对第 i 层的状态进行更新,将当前元素的 forward 指向新的节点
new_node.forward[i] = update[i].forward[i]
update[i].forward[i] = new_node
def erase(self, num: int) -> bool:
update = [None] * MAX_LEVEL
curr = self.head
for i in range(self.level - 1, -1, -1):
# 找到第 i 层小于且最接近 num 的元素
while curr.forward[i] and curr.forward[i].val < num:
curr = curr.forward[i]
update[i] = curr
curr = curr.forward[0]
if curr is None or curr.val != num: # 值不存在
return False
for i in range(self.level):
if update[i].forward[i] != curr:
break
# 对第 i 层的状态进行更新,将 forward 指向被删除节点的下一跳
update[i].forward[i] = curr.forward[i]
# 更新当前的 level
while self.level > 1 and self.head.forward[self.level - 1] is None:
self.level -= 1
return True