题目来源
189. 轮转数组

方法一：使用额外的数组

我们可以使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度，我们遍历原数组，将原数组下标为 i 的元素放至新数组下标为 (i+k) mod n 的位置，最后将新数组拷贝至原数组即可。
时间复杂度： O(n)
空间复杂度： O(n)

class Solution {
    public void rotate(int[] nums, int k) {
        int N = nums.length;
        int[] arr = new int[N];
        for (int i = 0; i < N; i++) {
            arr[(i+k)%N] = nums[i];
        }
        System.arraycopy(arr,0,nums,0,N);
    }
}

方法二：环状替换

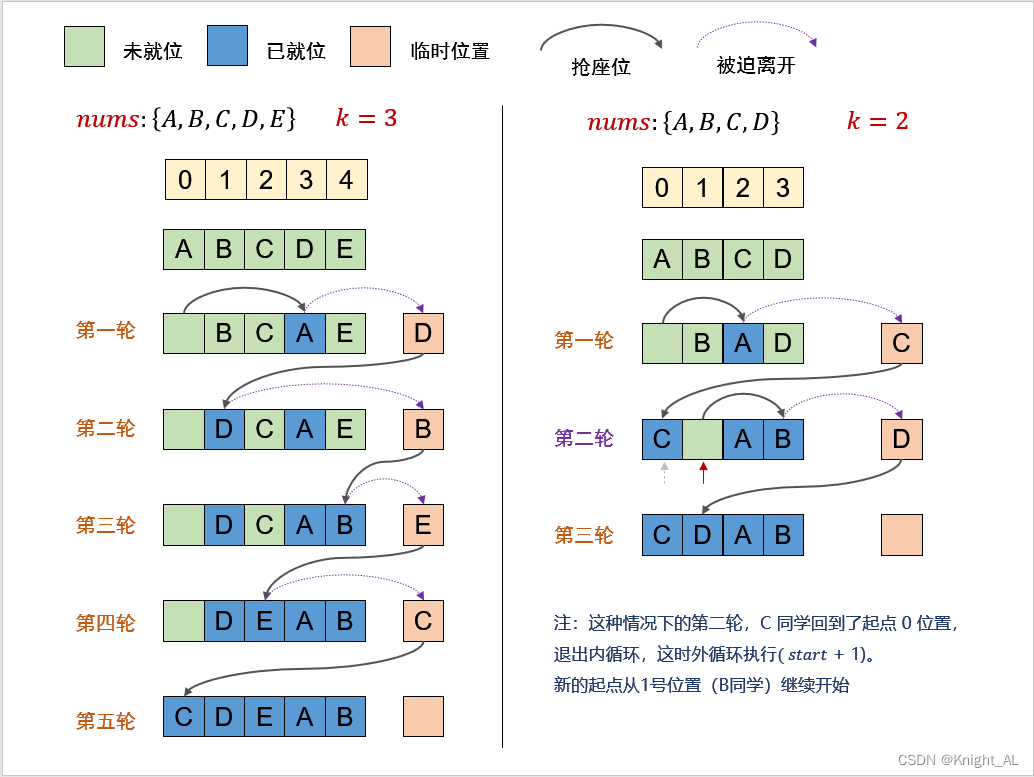
其实是这样的，对于一个长度为 nnn 的数组，整体移动 kkk 个位置
当 n 和 k 的最大公约数 等于 1 的时候：1 次遍历就可以完成交换；比如 n=5,k=3
当 n 和 k 的最大公约数 不等于 1 的时候：1 次遍历是无法完成的所有元素归位，需要 m (最大公约数) 次
时间复杂度：O(n)，其中 n 为数组的长度。每个元素只会被遍历一次。
空间复杂度：O(1)。我们只需常数空间存放若干变量。

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k = k % n;
        int count = 0;    // 记录交换位置的次数，n个同学一共需要换n次
        for (int start = 0; count < n; start++) {
            int cur = start;   // 从0位置开始换位子
            int pre = nums[cur];
            do {
                int next = (cur+k)%n;
                int temp = nums[next];   // 来到角落...
                nums[next] = pre;
                pre = temp;
                cur = next;
                count++;
            }while (start!=cur);    // 循环暂停，回到起始位置，角落无人
        }
    }
}

方法三：数组翻转

1.首先对整个数组实行翻转，这样子原数组中需要翻转的子数组，就会跑到数组最前面。
2.这时候，从 k 处分隔数组，左右两数组，各自进行翻转即可。

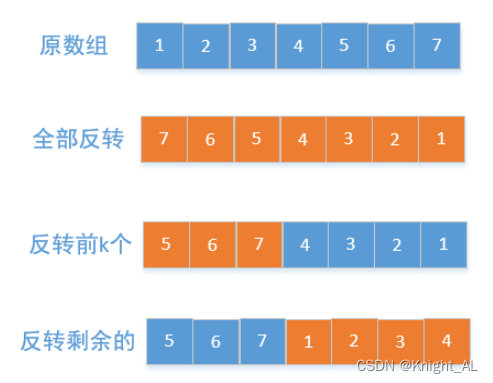
时间复杂度：O(n)，其中 nnn 为数组的长度。每个元素被翻转两次，一共 n 个元素，因此总时间复杂度为 O(2n)=O(n)。
空间复杂度：O(1)。

class Solution {
    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums,0,nums.length-1);
        reverse(nums,0,k-1);
        reverse(nums,k,nums.length-1);
    }

    private void reverse(int[] nums, int start, int end) {
        while (start < end){
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }
}