1合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

• 1 <= intervals.length <= 104
• intervals[i].length == 2
• 0 <= starti <= endi <= 104

思路:本题是判断重叠区间问题  先排序，让所有的相邻区间尽可能的重叠在一起，按左边界，或者右边界排序都可以.

1. 排序： 首先，根据每个区间的左边界，对给定的区间集合 intervals 进行升序排序。这是为了确保处理区间时，可以按顺序考虑它们的位置关系。

2. 合并过程： 排序完成后，使用一个结果集合 result 来存储最终合并后的区间。开始时，将排序后的第一个区间直接放入 result 中。

3. 遍历区间： 从第二个区间开始遍历，与 result 中的最后一个区间比较：

   • 如果当前区间与 result 中的最后一个区间有重叠（即当前区间的左边界小于等于 result 中最后一个区间的右边界），则更新 result 中最后一个区间的右边界为两者的最大值，以实现合并。
   • 如果当前区间与 result 中的最后一个区间没有重叠，则直接将当前区间加入 result。

代码

class Solution {
public:
    // 定义一个静态函数作为比较函数，用于排序
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0]; // 按照区间的左边界进行升序排序
    }
    
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> result;
        if (intervals.empty()) return result; // 如果区间集合为空直接返回空结果
        // 使用cmp函数对区间进行排序
        sort(intervals.begin(), intervals.end(), cmp);

        // 第一个区间直接放入结果集合中
        result.push_back(intervals[0]); 

        for (int i = 1; i < intervals.size(); i++) {
            if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间
                // 合并区间，只需要更新结果集合中最后一个区间的右边界
                result.back()[1] = max(result.back()[1], intervals[i][1]); 
            } else {
                result.push_back(intervals[i]); // 区间不重叠，将当前区间加入结果集合
            }
        }
        return result;
    }
};

2 单调递增的数字

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回 小于或等于 n 的最大数字，且数字呈 单调递增 。

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

提示:

• 0 <= n <= 109

思路:

举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。

那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

1. 将整数 N 转换为字符串 strNum，便于按位处理。
2. 从右向左遍历字符串 strNum，找到第一个出现递减的位置 i，即满足 strNum[i-1] > strNum[i]。
3. 将第 i-1 位减一，并标记 flag 为 i，表示从这里开始需要调整。
4. 将从 flag 开始的所有位置的字符设为 ‘9’，以确保得到最大的单调递增数。
5. 将处理后的字符串转换为整数并返回作为结果。

代码:

class Solution {
public:
    int monotoneIncreasingDigits(int N) {
        string strNum = to_string(N);
        // flag用来标记需要修改的位置，初始化为字符串长度，防止第二个循环在未赋值的情况下执行
        int flag = strNum.size();
        
        // 从倒数第二位开始向前遍历
        for (int i = strNum.size() - 1; i > 0; i--) {
            // 如果当前位大于前一位，则前一位需要减一，并更新flag
            if (strNum[i - 1] > strNum[i]) {
                flag = i; // 记录需要减一的位置
                strNum[i - 1]--; // 前一位减一
            }
        }
        
        // 将flag位置及之后的所有位数变为9，以获得最大的单调递增数
        for (int i = flag; i < strNum.size(); i++) {
            strNum[i] = '9';
        }
        
        return stoi(strNum); // 转换为整数并返回
    }
};

3监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

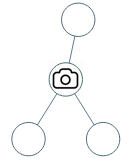
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

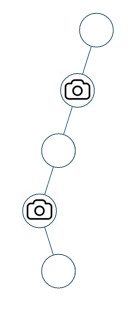
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

1. 给定树的节点数的范围是 [1, 1000]。
2. 每个节点的值都是 0。

思路:我们要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！可以使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了.

给定一个二叉树，节点状态有三种：未被覆盖、已被覆盖（无需额外摄像头）、已安装摄像头。目标是找出最少需要安装的摄像头数量，覆盖整棵树的所有节点。

定义递归函数 traversal，对当前节点进行处理：

• 如果左右子树有任意一个是未被覆盖的状态（返回2），则当前节点需要安装摄像头，返回1表示当前节点已安装摄像头。
• 如果左右子树都已被覆盖（返回0），则当前节点不需要额外的摄像头覆盖。
• 如果左右子树有一个已安装摄像头（返回1），则当前节点被覆盖，返回0。

1. 根节点处理： 调用 traversal 函数处理根节点。如果根节点未被覆盖（返回2），则需要额外安装一个摄像头。

2. 终返回 result，即安装摄像头的总数量。

代码: 

class Solution {
private:
    int result; // 记录需要安装摄像头的数量

    // 递归函数，返回当前节点的状态：
    // 0 - 节点已被覆盖
    // 1 - 节点安装了摄像头
    // 2 - 节点未被覆盖
    int traversal(TreeNode* cur) {
        if (cur == NULL) return 2; // 空节点默认已覆盖

        int left = traversal(cur->left);    // 处理左子树
        int right = traversal(cur->right);  // 处理右子树

        // 如果左右子树有任意一个未被覆盖，当前节点需要安装摄像头
        if (left == 2 || right == 2) {
            result++; // 安装摄像头
            return 1; // 当前节点已安装摄像头
        }
        // 如果左右子树的状态都是已覆盖，当前节点不需要额外摄像头覆盖
        else if (left == 0 && right == 0) {
            return 2; // 当前节点未被覆盖
        } else {
            return 0; // 当前节点已被覆盖
        }
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0; // 初始化摄像头数量为0
        if (traversal(root) == 2) { // 如果根节点未被覆盖，则需额外安装摄像头
            result++;
        }
        return result; // 返回最终需要安装的摄像头数量
    }
};