昇思25天学习打卡营第二天|初学入门/初学教程/03-张量

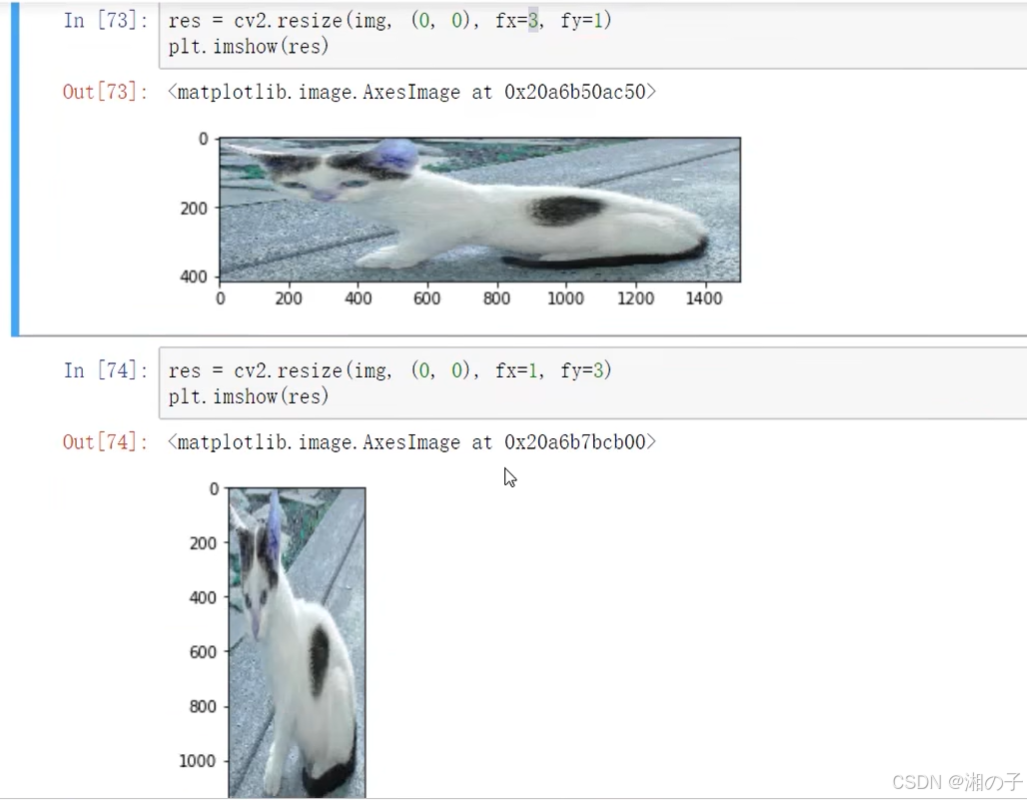
心得

补充一些基本知识帮助理解张量这个比较理论的概念：

张量（tensor）理论是数学的一个分支学科，在力学中有重要应用。张量这一术语起源于力学，它最初是用来表示弹性介质中各点应力状态的，后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要，在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广，矢量是一阶张量。

在数学里，张量是一种几何实体，或者说广义上的“数量”。张量概念包括标量、向量和线性算子。张量可以用坐标系统来表达，记作标量的数组，但它是定义为“不依赖于参照系的选择的”。张量在物理和工程学中很重要。例如在扩散张量成像中，表达器官对于水的在各个方向的微分透性的张量可以用来产生大脑的扫描图。

张量，这个概念由格雷戈里奥·里奇-库尔巴斯特罗在1890年在《绝对微分几何》的标题下发展出来，随着1900年列维-奇维塔的经典文章《绝对微分》（意大利文，随后出版了其他译本）的出版而为许多数学家所知。随着1915年左右爱因斯坦的广义相对论的引入，张量微积分获得了更广泛的承认。广义相对论完全由张量语言表述，爱因斯坦从列维-奇维塔本人那里学了很多张量语言（其实是Marcel Grossman，他是爱因斯坦在苏黎世联邦理工学院的同学，一个几何学家，也是爱因斯坦在张量语言方面的良师益友 - 参看Abraham Pais所著《上帝是微妙的（Subtle is the Lord）》），并学得很艰苦。

看了半天，越看越晕？

我来稍微初步理解一下，如果不对请指正，如果不完整，请补充，我也学习学习。从程序员的角度上理解，张量，就是一个数学结构。就和数组、列表、堆、栈、接口等一样，就是一个结构体或者类。里面有数据，也有功能函数。这个结构体可以用来描述图形对象，说白了就是照片。或者还有一些其他的一些对象？

学习打卡：

为csdn博客的后台程序员点个赞，居然可以直接粘贴图片！

张量 Tensor

张量（Tensor）是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数，这些线性关系的基本例子有内积、外积、线性映射以及笛卡儿积。其坐标在 𝑛𝑛 维空间内，有 𝑛𝑟𝑛𝑟 个分量的一种量，其中每个分量都是坐标的函数，而在坐标变换时，这些分量也依照某些规则作线性变换。𝑟𝑟 称为该张量的秩或阶（与矩阵的秩和阶均无关系）。

张量是一种特殊的数据结构，与数组和矩阵非常相似。张量（Tensor）是MindSpore网络运算中的基本数据结构，本教程主要介绍张量和稀疏张量的属性及用法。

[1]:

%%capture captured_output

# 实验环境已经预装了mindspore==2.3.0rc1，如需更换mindspore版本，可更改下面mindspore的版本号

!pip uninstall mindspore -y

!pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspore==2.3.0rc1

[2]:

import numpy as np

import mindspore

from mindspore import ops

from mindspore import Tensor, CSRTensor, COOTensor

创建张量

张量的创建方式有多种，构造张量时，支持传入Tensor、float、int、bool、tuple、list和numpy.ndarray类型。

根据数据直接生成

可以根据数据创建张量，数据类型可以设置或者通过框架自动推断。

[3]:

data = [1, 0, 1, 0]

x_data = Tensor(data)

print(x_data, x_data.shape, x_data.dtype)

[1 0 1 0] (4,) Int64

从NumPy数组生成

可以从NumPy数组创建张量。

[4]:

np_array = np.array(data)

x_np = Tensor(np_array)

print(x_np, x_np.shape, x_np.dtype)

[1 0 1 0] (4,) Int64

使用init初始化器构造张量

当使用init初始化器对张量进行初始化时，支持传入的参数有init、shape、dtype。
- init: 支持传入initializer的子类。如：下方示例中的 One() 和 Normal()。
- shape: 支持传入 list、tuple、 int。
- dtype: 支持传入mindspore.dtype。

[5]:

from mindspore.common.initializer import One, Normal

# Initialize a tensor with ones

tensor1 = mindspore.Tensor(shape=(2, 2), dtype=mindspore.float32, init=One())

# Initialize a tensor from normal distribution

tensor2 = mindspore.Tensor(shape=(2, 2), dtype=mindspore.float32, init=Normal())

print("tensor1:\n", tensor1)

print("tensor2:\n", tensor2)

tensor1:
 [[1. 1.]
 [1. 1.]]
tensor2:
 [[ 0.01346407 -0.01299477]
 [ 0.01350752 -0.0037052 ]]

init主要用于并行模式下的延后初始化，在正常情况下不建议使用init对参数进行初始化。

继承另一个张量的属性，形成新的张量

[6]:

from mindspore import ops

x_ones = ops.ones_like(x_data)

print(f"Ones Tensor: \n {x_ones} \n")

x_zeros = ops.zeros_like(x_data)

print(f"Zeros Tensor: \n {x_zeros} \n")

Ones Tensor: 
 [1 1 1 1] 

Zeros Tensor: 
 [0 0 0 0]

张量的属性

张量的属性包括形状、数据类型、转置张量、单个元素大小、占用字节数量、维数、元素个数和每一维步长。

形状（shape）：Tensor的shape，是一个tuple。
数据类型（dtype）：Tensor的dtype，是MindSpore的一个数据类型。
单个元素大小（itemsize）： Tensor中每一个元素占用字节数，是一个整数。
占用字节数量（nbytes）： Tensor占用的总字节数，是一个整数。
维数（ndim）： Tensor的秩，也就是len(tensor.shape)，是一个整数。
元素个数（size）： Tensor中所有元素的个数，是一个整数。
每一维步长（strides）： Tensor每一维所需要的字节数，是一个tuple。

[7]:

x = Tensor(np.array([[1, 2], [3, 4]]), mindspore.int32)

print("x_shape:", x.shape)

print("x_dtype:", x.dtype)

print("x_itemsize:", x.itemsize)

print("x_nbytes:", x.nbytes)

print("x_ndim:", x.ndim)

print("x_size:", x.size)

print("x_strides:", x.strides)

x_shape: (2, 2)
x_dtype: Int32
x_itemsize: 4
x_nbytes: 16
x_ndim: 2
x_size: 4
x_strides: (8, 4)

张量索引

Tensor索引与Numpy索引类似，索引从0开始编制，负索引表示按倒序编制，冒号:和 ...用于对数据进行切片。

[8]:

tensor = Tensor(np.array([[0, 1], [2, 3]]).astype(np.float32))

print("First row: {}".format(tensor[0]))

print("value of bottom right corner: {}".format(tensor[1, 1]))

print("Last column: {}".format(tensor[:, -1]))

print("First column: {}".format(tensor[..., 0]))

First row: [0. 1.]
value of bottom right corner: 3.0
Last column: [1. 3.]
First column: [0. 2.]

张量运算

张量之间有很多运算，包括算术、线性代数、矩阵处理（转置、标引、切片）、采样等，张量运算和NumPy的使用方式类似，下面介绍其中几种操作。

普通算术运算有：加（+）、减（-）、乘（*）、除（/）、取模（%）、整除（//）。

[9]:

x = Tensor(np.array([1, 2, 3]), mindspore.float32)

y = Tensor(np.array([4, 5, 6]), mindspore.float32)

output_add = x + y

output_sub = x - y

output_mul = x * y

output_div = y / x

output_mod = y % x

output_floordiv = y // x

print("add:", output_add)

print("sub:", output_sub)

print("mul:", output_mul)

print("div:", output_div)

print("mod:", output_mod)

print("floordiv:", output_floordiv)

add: [5. 7. 9.]
sub: [-3. -3. -3.]
mul: [ 4. 10. 18.]
div: [4.  2.5 2. ]
mod: [0. 1. 0.]
floordiv: [4. 2. 2.]

concat将给定维度上的一系列张量连接起来。

[10]:

data1 = Tensor(np.array([[0, 1], [2, 3]]).astype(np.float32))

data2 = Tensor(np.array([[4, 5], [6, 7]]).astype(np.float32))

output = ops.concat((data1, data2), axis=0)

print(output)

print("shape:\n", output.shape)

[[0. 1.]
 [2. 3.]
 [4. 5.]
 [6. 7.]]
shape:
 (4, 2)

stack则是从另一个维度上将两个张量合并起来。

[11]:

data1 = Tensor(np.array([[0, 1], [2, 3]]).astype(np.float32))

data2 = Tensor(np.array([[4, 5], [6, 7]]).astype(np.float32))

output = ops.stack([data1, data2])

print(output)

print("shape:\n", output.shape)

[[[0. 1.]
  [2. 3.]]

 [[4. 5.]
  [6. 7.]]]
shape:
 (2, 2, 2)

Tensor与NumPy转换

Tensor可以和NumPy进行互相转换。

Tensor转换为NumPy

与张量创建相同，使用 Tensor.asnumpy() 将Tensor变量转换为NumPy变量。

[12]:

t = Tensor([1., 1., 1., 1., 1.])

print(f"t: {t}", type(t))

n = t.asnumpy()

print(f"n: {n}", type(n))

t: [1. 1. 1. 1. 1.] <class 'mindspore.common.tensor.Tensor'>
n: [1. 1. 1. 1. 1.] <class 'numpy.ndarray'>

NumPy转换为Tensor

使用Tensor()将NumPy变量转换为Tensor变量。

[13]:

n = np.ones(5)

t = Tensor.from_numpy(n)

[14]:

np.add(n, 1, out=n)

print(f"n: {n}", type(n))

print(f"t: {t}", type(t))

n: [2. 2. 2. 2. 2.] <class 'numpy.ndarray'>
t: [2. 2. 2. 2. 2.] <class 'mindspore.common.tensor.Tensor'>

稀疏张量

稀疏张量是一种特殊张量，其中绝大部分元素的值为零。

在某些应用场景中（比如推荐系统、分子动力学、图神经网络等），数据的特征是稀疏的，若使用普通张量表征这些数据会引入大量不必要的计算、存储和通讯开销。这时就可以使用稀疏张量来表征这些数据。

MindSpore现在已经支持最常用的CSR和COO两种稀疏数据格式。

常用稀疏张量的表达形式是<indices:Tensor, values:Tensor, shape:Tensor>。其中，indices表示非零下标元素， values表示非零元素的值，shape表示的是被压缩的稀疏张量的形状。在这个结构下，我们定义了三种稀疏张量结构：CSRTensor、COOTensor和RowTensor。

CSRTensor

CSR（Compressed Sparse Row）稀疏张量格式有着高效的存储与计算的优势。其中，非零元素的值存储在values中，非零元素的位置存储在indptr（行）和indices（列）中。各参数含义如下：

indptr: 一维整数张量, 表示稀疏数据每一行的非零元素在values中的起始位置和终止位置, 索引数据类型支持int16、int32、int64。
indices: 一维整数张量，表示稀疏张量非零元素在列中的位置, 与values长度相等，索引数据类型支持int16、int32、int64。
values: 一维张量，表示CSRTensor相对应的非零元素的值，与indices长度相等。
shape: 表示被压缩的稀疏张量的形状，数据类型为Tuple，目前仅支持二维CSRTensor。

CSRTensor的详细文档，请参考mindspore.CSRTensor。

下面给出一些CSRTensor的使用示例：

[15]:

indptr = Tensor([0, 1, 2])

indices = Tensor([0, 1])

values = Tensor([1, 2], dtype=mindspore.float32)

shape = (2, 4)

# Make a CSRTensor

csr_tensor = CSRTensor(indptr, indices, values, shape)

print(csr_tensor.astype(mindspore.float64).dtype)

Float64

上述代码会生成如下所示的CSRTensor:

[10020000][10000200]

COOTensor

COO（Coordinate Format）稀疏张量格式用来表示某一张量在给定索引上非零元素的集合，若非零元素的个数为N，被压缩的张量的维数为ndims。各参数含义如下：

indices: 二维整数张量，每行代表非零元素下标。形状：[N, ndims]，索引数据类型支持int16、int32、int64。
values: 一维张量，表示相对应的非零元素的值。形状：[N]。
shape: 表示被压缩的稀疏张量的形状，目前仅支持二维COOTensor。

COOTensor的详细文档，请参考mindspore.COOTensor。

下面给出一些COOTensor的使用示例：

[16]:

indices = Tensor([[0, 1], [1, 2]], dtype=mindspore.int32)

values = Tensor([1, 2], dtype=mindspore.float32)

shape = (3, 4)

# Make a COOTensor

coo_tensor = COOTensor(indices, values, shape)

print(coo_tensor.values)

print(coo_tensor.indices)

print(coo_tensor.shape)

print(coo_tensor.astype(mindspore.float64).dtype)  # COOTensor to float64

[1. 2.]
[[0 1]
 [1 2]]
(3, 4)
Float64

上述代码会生成如下所示的COOTensor:

000100020000[010000200000]

[17]:

import time

print(time.strftime("%Y-%m-%d %H:%M:%S", time.localtime()),'guojun0718')

2024-07-12 00:34:09 guojun0718

[ ]: