一. 归并排序

1.1 归并排序的实现思想

归并排序采用分治的思想实现，对于具有n个数据的待排序数组，先将其前半部分和后半部分都排列为有序，然后将前半部分和后半部分视为不同的两个有序序列，将这两个有序序列合并，得到的新的有序序列就是原序列排序后的结果。图1.1展示了归并排序的实现过程。

由图1.1，为了保证前半部分和后半部分有序，在将数组拆分为两部分后继续拆分，直到每组数据中仅有一个数据，单个数据可视为有序序列。完成整体拆分后，即拆到每组只有一个数据，将数据合并为每组两个数据，每组的两个数据有序，之后继续执行合并操作，直到数组中所有数据有序。

1.2 归并排序的递归实现

1.2.1 归并排序递归实现的思想

定义一个主递归排序函数MergeSort，其参数包括待排序数组a和数据个数n，在Mergesort函数中要开辟一块内存空间tmp临时存储部分排好序的数据，还要再调用一个子函数_MergeSort，这个函数的功能是将下标[left, right]之间的数据采用归并排序的方式排好。
_MergeSort函数对[left,right]之间的数据排序。取mid=(left+right)/2，应当保证[left,mid]以及[mid+1,right]之间的数据有序，为此，采用递归的方法，对[left,right]之间的数据进行拆分，直到保证每组只有一个数据时才开始排序合并。因此，递归的终止条件为：left<=right。
分组对数据进行合并，直到整个数组中的数据有序。

1.2.2 归并排序递归实现的代码

void _MergeSort(int* a, int* tmp, int left, int right)
{
	//如果区间左值大于等于区间右值，停止拆分
	if (left >= right)
	{
		return;
	}

	int mid = (left + right) / 2;

	_MergeSort(a, tmp, left, mid);  //左区间归并排序
	_MergeSort(a, tmp, mid + 1, right);  //右区间归并排序

	//区间[left,mid] [mid+1,right]中的数据均有序
	//合并两组数据成新的有序序列
	int begin1 = left, end1 = mid;  //左区间的起始下标和结束下标
	int begin2 = mid + 1, end2 = right;  //右区间的起始下标和结束下标
	
	//排升序
	int index = begin1;  //控制tmp的下标

	//先将[left,right]区间的数据按顺序排序存入tmp的[left,right]，然后拷贝会原数组a
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}

	//将tmp中的数据拷贝回a
	for (int i = left; i <= right; ++i)
	{
		a[i] = tmp[i];
	}
}

void MergeSort(int* a, int n)  //递归实现归并排序函数
{
	assert(a);

	//开辟临时空间存储用于临时存储部分排序后的数据
	int* tmp = (int*)malloc(n * sizeof(int)); 
	if (NULL == tmp)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	_MergeSort(a, tmp, 0, n - 1);

	free(tmp);
	tmp = NULL;
}

1.3 归并排序的非递归实现

1.3.1 归并排序非递归实现的思想

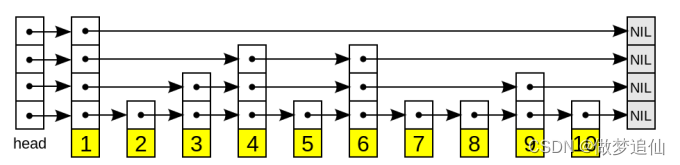
归并排序的非递归实现思想与递归类似，都是先将待排序数组中的有数据分组，先将数组中的每个数据单独视为一组，从左侧第一组数据开始，将每两个数据合并为新的组，然后继续按组合并数据，直到完成排序。

与递归不同的是，非递归引入变量gap来控制两组待合并的有序序列首元素的下标之差。如图1.2所示，取begin1和end1分别为左侧有序序列起始下标和结束下标，取begin2和end2位右侧有序序列的起始下标和结束下标，程序中用循环参数i来控制左侧有序序列起始下标，因此：左侧有序序列下标范围[i, i+gap-1]，即[begin1,end1]，右侧有序序列下标范围是[i+gap,i+2*gap-1]，即[begin2,end2]。将左右两边的有序序列合并，使区间[begin1,end2]之间的数据有序。

更新gap的值依次为2、4、8、....，重复执行上段叙述的操作，直到gap<n不成立为止（n为待排序数据的个数）。

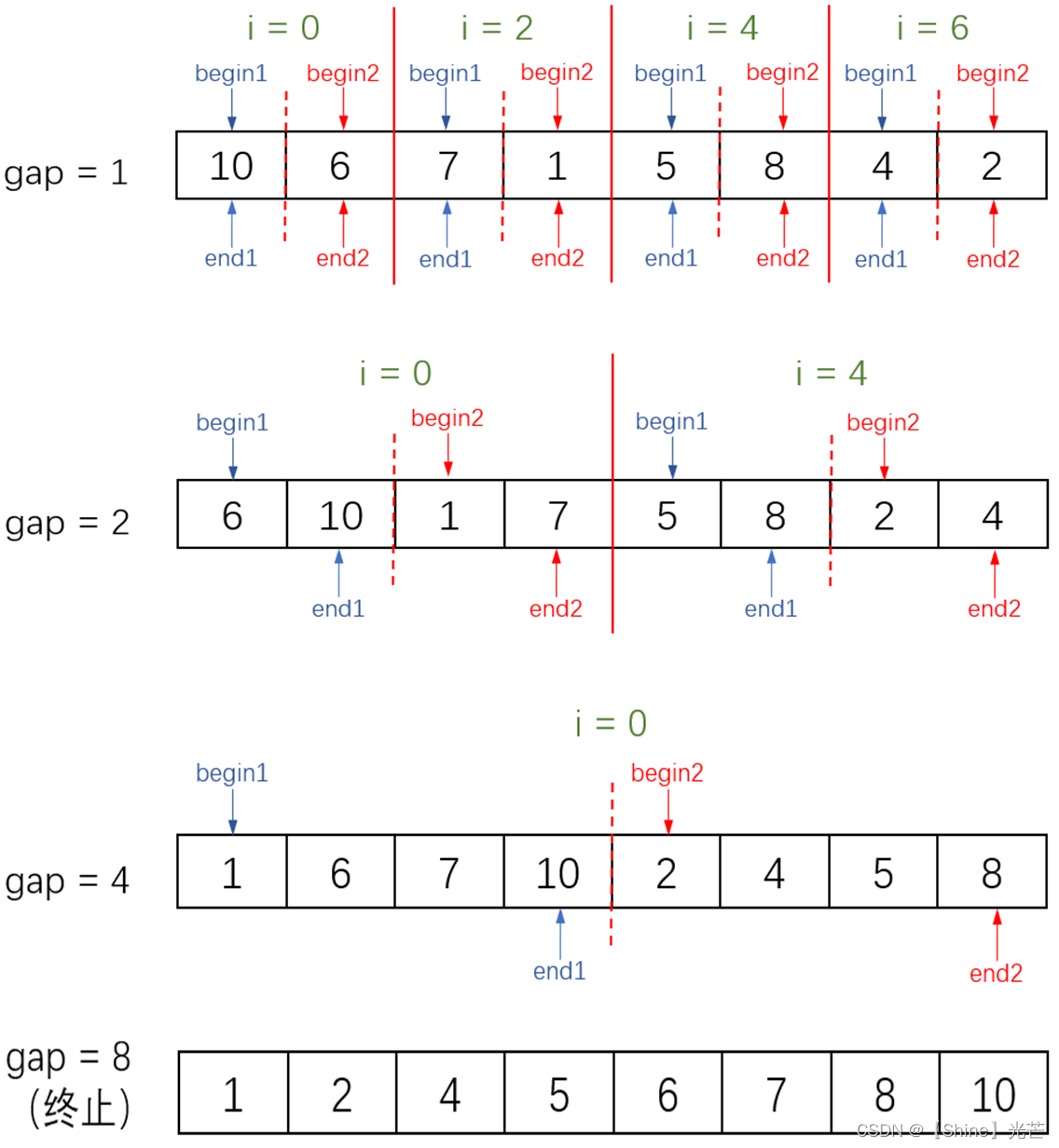
图1.2展示的数组有n=8个数据，满足 $n=2^i$ ，因此，begin1、end1、begin2、end2全部没有发生越界，但是，如果待排序数据个数不满足 $n=2^i$ ，那么end1、begin2、end2则有可能发生越界，begin1一定不会发生越界。越界可分三种情况进行讨论：

end1、begin2、end2均越界。
end1不越界，begin2和end2越界。
end1和begin2不越界，end2越界。

图1.3展示了两种越界情况，当对7个数据进行排序时，gap=1时存在end1不越界，begin2和end2越界的情况，gap=2时存在end1和end2均越界，end2越界的情况。

对于越界的处理可以分为两种情况讨论：

对于end1、begin2、end2均越界的情况以及end1不越界，begin2和end2越界的情况，区间[begin2,end2]不存在，无需从临时存储数据的区间tmp中拷贝数据回原数组，此时直接break掉本次循环即可。
对于end1和begin2不越界，end2越界的情况，调整end2=n-1，使区间[begin2,end2]不再越界即可。

处理完越界的情况，即可执行两有序序列的合并操作，直到排序完成。

1.3.2 归并排序非递归实现的代码

//归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
	assert(a);

	int* tmp = (int*)malloc(n * sizeof(int));  //临时存储排序好的数据
	if (NULL == tmp)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	int gap = 1; //左右两侧的有序序列下标差
	while (gap < n)
	{
		int i = 0;  //循环参数

		for (i = 0; i < n; i += 2 * gap)
		{
			//划分左右两侧区间的起始下标和终止下标
			//左侧：[begin1,end1]，右侧：[begin2,end2]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//当end1越界或begin2越界时，[begin2,end2]不存在，无需从tmp中拷贝数据
			//此时终止循环即可
			if (end1 >= n || begin2 >= n)
			{
				break;
			}

			//仅有end2越界，end1和begin2不越界，[begin2,end2]存在
			//此时修改end2的值，使其不越界即可
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			//将[begin1,end1] [begin2,end2]两有序数据整合为一个有序序列
			int index = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin2] < a[begin1])
				{
					tmp[index++] = a[begin2++];
				}
				else
				{
					tmp[index++] = a[begin1++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}

			//将tmp中区间[begin1,end2]之间的数据拷贝回原数组a的对应区间
			int j = i;
			for (j = i; j <= end2; ++j)
			{
				a[j] = tmp[j];
			}
		}

		gap *= 2;  //更新gap
	}

	free(tmp);
	tmp = NULL;
}

1.4 归并排序的时间复杂度分析

假设待排序的数据个数为N，观察图1.1可得，总共需要被拆分为 $logN$ 层，拆分完成后逐层进行合并，每层合并需要遍历全部待排序数据，即每层要遍历数据N次，因此，整个合并过程要执行的操作次数可以近似认为是 $NlogN$ ，拆分过程执行的操作相对于合并过程可以忽略不计。因此，归并排序的时间复杂度为： $O(NlogN)$ 。

二. 计数排序

2.1 计数排序的思想

计数排序采用的是映射的思想，假设一组待排序数组中数据的最小值为min，最大值为max，开辟一块计数数组空间*count，其中count的空间大小应能存储range=max-min+1个数据，count[0]的值为最小值min出现的次数，count[1]的值为次小值出现的次数，...，count[range]为最大值max出现的次数。根据count中每个数据的值对数据进行排序。

如图2.1所示，对数组a[] = {-2,0,0,0,2,2,3}进行排序，其中min=-2，max=3，因此count应该能容纳range = 3-(-2)+1=6个数据。数组a中，-2对应count下标为0的位置，-2出现一次，因此count[0]=1，-1对应下标为1的位置，-1出现0次，因此count[1]=0。count[6]={1,0,3,0,2,1}。

2.2 计数排序函数代码

//计数排序函数
void CountSort(int* a, int n)
{
	assert(a);

	int min = a[0];
	int max = a[0];   //数组a中最大值和最小值

	//获取数组中的最大值和最小值
	int i = 0;
	for (i = 1; i < n; ++i)
	{
		if (a[i] > max)
		{
			max = a[i];
		}

		if (a[i] < min)
		{
			min = a[i];
		}
	}

	int range = max - min + 1;  //数据的范围
	int* count = (int*)malloc(range * sizeof(int));  //计数数组
	if (NULL == count)
	{
		perror("malloc");
		exit(-1);
	}
	memset(count, 0, range * sizeof(int));  //计数数组所有元素初始化为0

	for (i = 0; i < n; ++i)
	{
		count[a[i] - min]++;
	}

	//将count中的计数情况拷贝回原数组a
	int index = 0;
	for (i = 0; i < range; ++i)
	{
		while (count[i]--)
		{
			a[index++] = i + min;
		}
	}

	free(count);
	count = NULL;
}

2.3 计数排序的时间复杂度、空间复杂度及适用情况分析

假设要对N个数据进行排序，计数排序首先要遍历一遍待排序数据获取计数数组count，遍历待排序数据的时间复杂度为 $O(N)$ ，生成count后，要再遍历一遍count以获取排序后的序列，count中含有的数据个数为range=max-min+1，遍历count数组的时间复杂度为 $O(range)$ ，因此：计数排序的时间复杂度为 $O(max(N,range))$ ，空间复杂度为 $O(range)$ 。