题目

110. 平衡二叉树 - 力扣（LeetCode）

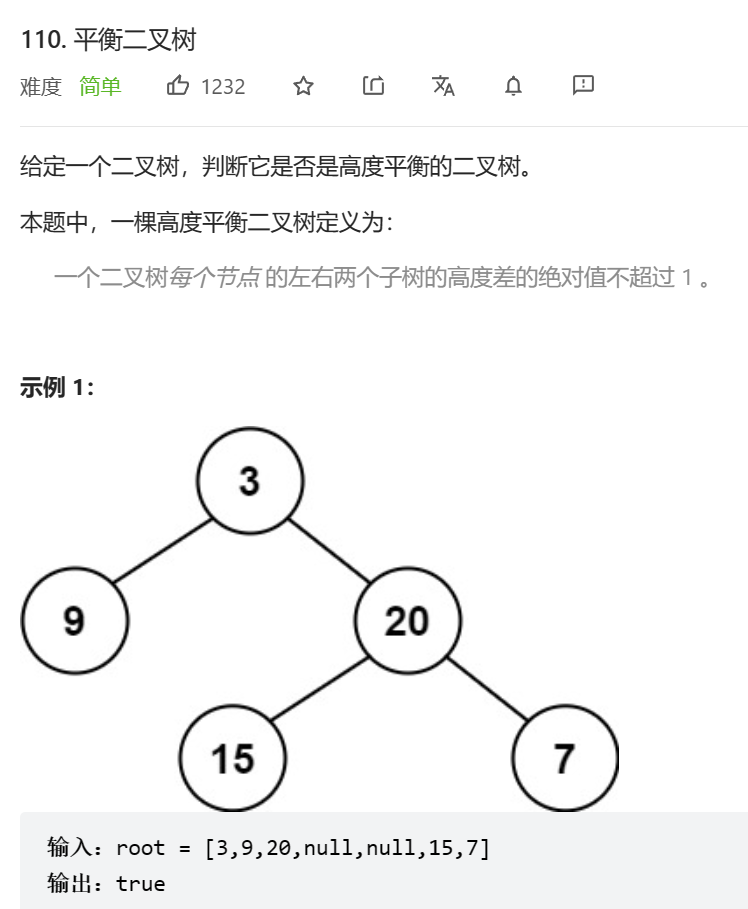
注意事项

首先我们要注意到，该题的意思是所有节点的高度差不超过一，而不是只有根节点的高度差不超过一，例如：

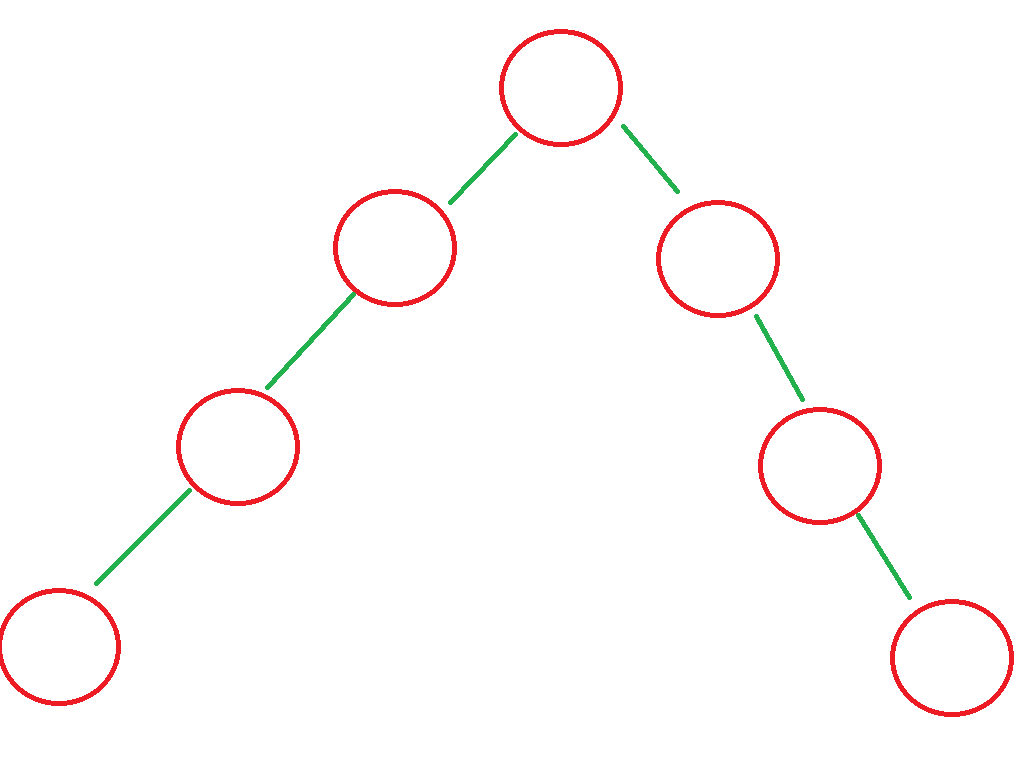
错误示例

上图显然不符合题目要求。

那么我们再来思考一下，如果树为空的情况，显然是符合题目要求的。

实现代码

根据上面的意思，转换为代码就是这样：

bool isBalanced(struct TreeNode* root)
{
    if(root == NULL)
    {
        return true;
    }
}

但是这样显然不够，只是判断了树为空的情况。

那么我们在树非空的情况下要想判断是否为平衡树，最好的方法是写一个计算树深度的函数。

我找到一个题目专门计算深度的，感兴趣的可以看一下哦！

题目：104. 二叉树的最大深度 - 力扣（LeetCode）

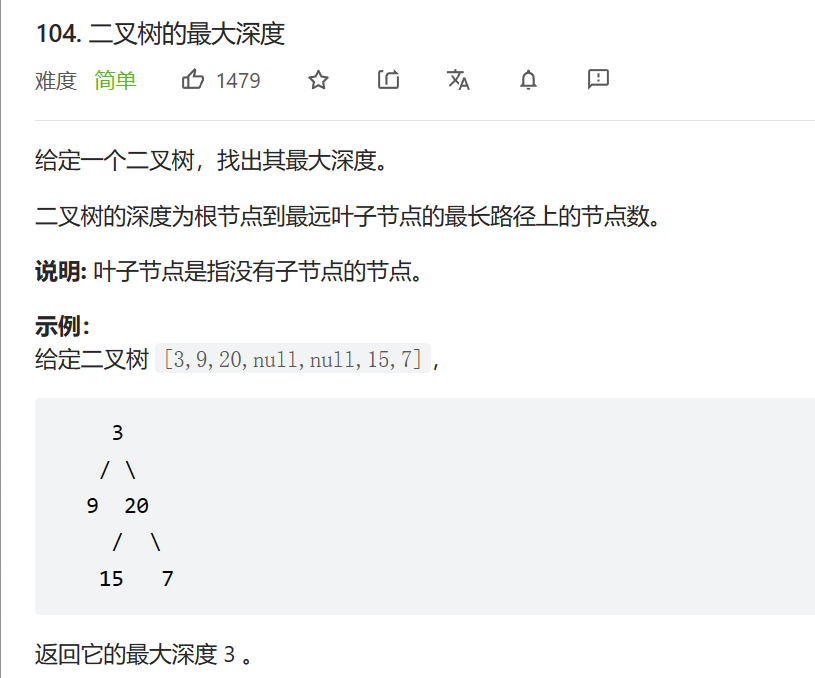
那么我们把计算深度的函数解决了，就顺便解决了上题。

其实我们在学习二叉树的时候写过一个计数函数，大家可以参考一下：

参考文献：二叉树（三）_染柒_GRQ的博客-CSDN博客

//法三：
int TreeSize(BTDNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

这里是计算节点和左右子树之和，而本题是要计算左子树与右子树的差，所以我们在写代码的时候只要写左子树加节点或者右子树加节点就行了。

当然这里不推荐三目运算符，比较麻烦。

//计算深度
int maxDepth(struct TreeNode* root)
{
    if(root ==  NULL)
    {
        return 0;
    }
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);
    return leftDepth > rightDepth ? leftDepth + 1: rightDepth + 1;
}

leftDepth 和rightDepth 是为了避免在递归过程中被替换掉。

最后我们在进行比较就行了。

bool isBalanced(struct TreeNode* root)
{
    if(root == NULL)
    {
        return true;
    }
    int leftDepth = maxDepth(root->left);
    int rightDepth = maxDepth(root->right);
    //比较
    return abs(leftDepth - rightDepth) < 2
    && isBalanced(root->left)
    && isBalanced(root->right);
}

注意：”abs“是计算绝对值的函数。