算法导论总结索引 | 第五部分第十八章：B树

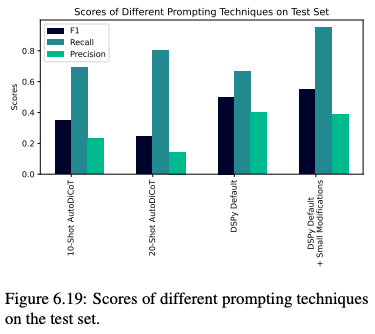
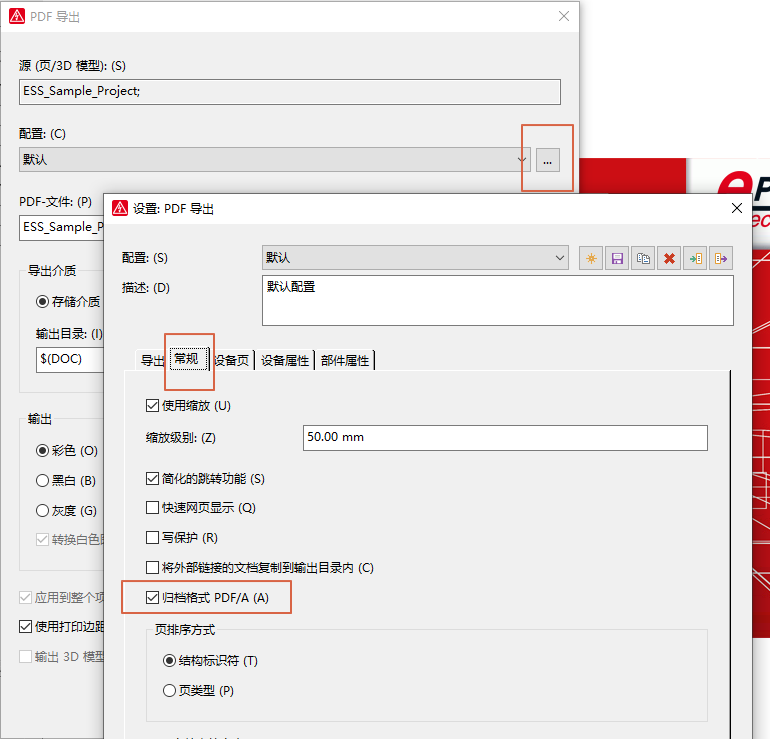
1、B 树是为磁盘或其他直接存取的辅助存储设备而设计的一种平衡搜索树。B 树类似于红黑树，在降低磁盘 I/O 操作次数方面要更好一些。许多数据库系统使用 B 树或者 B 树的变种来存储信息

2、B 树与红黑树的不同之处在于 B 树的结点可以有很多孩子，尽管它通常依赖于所使用的磁盘单元的特性。B 树类似于红黑树，每棵含有 n 个结点的 B 树的高度为 O(lgn)。一棵 B 树的严格高度可能比一棵红黑树的高度要小许多, 这是因为它的分支因子，也就是表示高度的对数的底数可以非常大
也可以使用 B 树在时间 O(lgn) 内完成一些动态合并的操作

3、如果 B 树的一个内部结点 x 包含 x.n 个关键字，那么结点 x 就有 n+1 个孩子。结点 x 中的关键字就是分隔点

当在一棵 B 树中查找一个关键字时，基于对存储在 x 中的 x.n 个关键字的比较，做出一个 (x.n + 1) 路的选择
在这里插入图片描述
4、为了掩还机械移动所花费的等待时间，磁盘会一次存取多个数据项而不是一个。信息被分为一系列等大小的在柱面内连续出现的页面，并且每个磁盘读或写一个或多个完整的页面

定位到一页信息并将其从磁盘里读出的时间要比对读出信息进行检查的时间要长得多。对运行时间的两个主要组成成分分别加以考虑：

磁盘存取次数
CPU (计算) 时间

使用需要读出或写入磁盘的信息的页数来衡量磁盘存取次数。磁盘存取时间并不是常量——它依赖于当前磁道和所需磁道之间的距离以及磁盘的初始旋转状态。仍使用读或写的页数作为磁盘存取总时间的主要近似值

在一个典型的 B 树应用中，所要处理的数据量非常大，以至于所有数据无法一次装入主存。B 树算法将所需页面从磁盘复制到主存，然后将修改过的页面写回到磁盘，任何时刻，B树算法都只需在主存中保持一定数量的页面

5、设 x 为指向一个对象的指针。如果该对象正在主存中，那么可以像平常一样引用该对象的各个属性：如 x.key。如果 x 所指向的对象驻留在磁盘上，那么在引用它的属性之前，必须先执行 DISK-READ(x)，将该对象读入主存中。(假设如果 x 已经在主存中，那么 DISK-READ(x) 不需要磁盘存取，即它是一个空操作。) 类似地，操作 DISK-WRITE(x) 用来保存对象 x 的属性所做的任何修改

x = a pointer to some object
DISK-READ(x)
operations that access and/or modify the attributes of x
DISK-WRITE(x) // omitted if no attributes of x were changed
other operations that access but do not modify attributes of x

6、在任何时候，这个系统可以在主存中只保持有限的页数。假定系统不再将被使用的页从主存中换出；后面的 B 树算法会忽略这一点

在大多数系统中, 一个 B 树算法的运行时间主要由它所执行的 DISK-READ 和 DISK-WRITE 操作的次数决定，所以希望这些操作能够读或写尽可能多的信息。因此，一个 B 树结点通常和一个完整磁盘页一样大，并且磁盘页的大小限制了一个 B 树结点可以含有的孩子个数

分支因子在 50~2000 之间，具体取决于一个关键字相对于一页的大小。一个大的分支因子可以大大地降低树的高度以及查找任何一个关键字所需的磁盘存取次数

由于根结点可以持久地保存在主存中，所以在这棵树中查找某个关键字至多只需两次磁盘存取
在这里插入图片描述

1、B 树的定义

1、任何和关键字相关系的卫星数据将与关键字一样存放在同一个结点中。可能只是为每个关键字存放一个指针，这个指针指向存放该关键字的卫星数据的磁盘页
这一章的伪代码都隐含地假设了当一个关键字从一个结点移动到另一个结点时，无论是与关键字相关的卫星数据，还是指向卫星数据的指针，都会随着关键字一起移动。一个常见的 B 树变种，称为 B+ 树，它把所有的卫星数据都存储在叶结点中，内部结点只存放关键字和孩子指针，因此最大化了内部结点的分支因子

2、一棵 B 树 T 是具有以下性质的有根树
1）每个结点 x 有下面属性：

x.n，当前存放在结点 x 中的关键字个数
x.n 个关键字本身 x.key_1，x.key_2，…，x.key_x.n，以非降序存放，使得 x.key_1 ≤ x.key_2 ≤ … ≤ x.key_x.n
x.leaf，一个布尔值。如果 x 是叶结点，则为 TRUE；如果 x 是内部结点，则为 FALSE

2）每个内部结点 x 还包含 x.n+1 个指向其孩子的指针 x.c_1，x.c_2，…，x.c_n+1。叶结点没有孩子，所以它们的 c_i 属性没有定义

3）关键字 x.key 将存储在各子树中的关键字范围加以分割：如果 k_i 为任意一个存储在以 x.c 为根的子树中的关键字，那么
在这里插入图片描述
4）每个叶结点具有相同的深度, 即树的高度 h

5）每个结点所包含的关键字个数有上界和下界。用一个数称为 B 树的最小度数（子树的数量）的固定整数 t ≥ 2 来表示这些界：

除了根结点以外的每个内部结点必须至少有 t - 1 个关键字。因此，除了根结点以外的每个内部结点至少有 t 个孩子。如果树非空，根结点至少有一个关键字
每个结点至多可包含 2t - 1 个关键字。因此，一个内部结点至多可有 2t 个孩子（因为超过 2t 就要分裂了）。当一个结点恰好有 2t - 1 个关键字时，称该结点是满的

t = 2 是 B 树最简单的。每个内部结点有 2 个、3 个或 4 个孩子，即一棵 2-3-4 树。t 的值越大, B 树的高度越小

3、B 树的高度：B 树上大部分的操作所需的磁盘存取次数与 B 树的高度是成正比的

如果 n ≥ 1，那么对任意一棵包含 n 个关键字，高度为 h，最小度数 t ≥ 2 的 B 树 T, 有
在这里插入图片描述
B 树 T 的根至少包含一个关键字，而且所有其他的结点至少包含 t - 1 个关键字。因此，高度为 h 的 B 树 T 在深度 1 至少包含 2 个结点（根有1个关键字），在深度 2 至少包含 2t 个结点, 在深度 3 至少包含 2t² 个结点，等等，直到深度 h 至少有 2t^h−1 结点。关键字的个数 n 满足不等式：（从第1层开始就要多乘个(t - 1)）
在这里插入图片描述
可以得到 t^h <= (n + 1)/2。两边取以 t 为底的对数就证明了定理

与红黑树对比，看到了 B 树的能力。尽管二者的高度都以 O(lg n) 的速度增长 (注意 t 是个常数)，但对 B 树来说，对数的底可以大很多倍。因此，对大多数树的操作来说，要检查的结点数在 B 树中要比红黑树中少大约 lgt 的因子。由于在一棵树中检查任意一个结点都需要一次磁盘访问，所以 B 树避免了大量的磁盘访问

4、为什么不允许最小度数 t = 1： B 树中不存在只有 0 个键的节点，也不存在只有 1 个子节点的节点

当 t 取何值时，图示的树是一棵合法的 B 树
在这里插入图片描述
除根节点外的每个节点必须至少有 t−1 个键，并且最多可以包含 2t−1 个键。每个节点（除了根节点）的键的数量要么是2，要么是3。因此，为了使其成为合法的B树，需要保证 t−1≤2 并且 2t−1≥3，这意味着 2≤t≤3。所以 t 可以是2或者3

5、如果红黑树中的每个黑结点吸收它的红色孩子，并把它们的孩子并作为自己的孩子，描述这个结果的数据结构
将每个红色节点吸收到其黑色父节点中后，每个黑色节点可能包含 1 或 2 个（1 个红色子节点），或者 3 个（2 个红色子节点）键，并且根据红黑树的性质5（对于每个节点，从该节点到后代叶节点的所有路径都包含相同数量的黑色节点），结果树的所有叶节点具有相同的深度。因此，一棵红黑树将变成最小度数为 t=2 的 B 树（因为红黑树是二叉树），即 2-3-4 树

2、B 树的基本操作（搜索、创建、插入）

1、给出 B-TREE-SEARCH、B-TREE-CREATE 和 B-TREE-INSERT 操作的细节，采用两个约定：

B 树的根结点始终在主存中，这样无需对根做 DISK-READ 操作；然而，当根结点被改变后, 需要对根结点做一次 DISK-WRITE 操作
任何被当做参数的结点在被传递之前，都会对它们先做一次 DISK-READ 操作

2、搜索 B 树：根据结点的孩子数做多路分支选择。对每个内部结点 x，做的是一个 (x.n + 1) 路的分支选择

输入是一个指向某子树根结点 x 的指针，以及要在该子树中搜索的一个关键字 k。顶层调用的形式为 B-TREE-SEARCH (T.root, k)。如果 k 在 B 树中，那么 B-TREE-SEARCH 返回的是由结点 y 和使得 x.key_i = k 的下标 i 组成的有序对 (y, i)；否则，过程返回 NIL

B-TREE-SEARCH(x, k)
1 i = 1
2 while i ≤ x.n and k > x.key_i
3 	i = i + 1
4 if i ≤ x.n and k == x.key_i
5 	return (x, i)
6 elseif x.leaf
7 	return NIL
8 else DISK-READ(x, c_i) // c_i指向第i个孩子的结点
9 	return B-TREE-SEARCH(x.c_i, k)

第 1 ~ 3 行找出最小下标 i, 使得 k ≤ x.key_i。若找不到，则 i = x.n + 1。第 4 ~ 5 行检查是否已经找到关键字 k, 如果找到，则返回；否则，第 6 ~ 9 行指定这次不成功查找 (如果 x 是叶结点)，或者在对孩子结点执行必要的 DISK-READ 后，递归搜索 x 相应子树

在递归过程中所遇到的结点构成了一条从树根向下的简单路径。因此，由 B-TREE-SEARCH 过程访问的磁盘页面数为 O(h) = O(logt(n))，其中 h 为 B 树的高度, n 为 B 树中所有关键字个数。由于 x.n < 2t，因此第 2 ~ 3 行的 while 循环在每个结点花费的时间为 O(t)，总的 CPU 时间为 O(th) = O(t logt(n))

3、创建一棵空的 B 树
辅助过程 ALLOCATE-NODE，它在 O(1) 时间内为一个新结点分配一个磁盘页。可以假定由 ALLOCATE-NODE 所创建的结点并不需要 DISK-READ，因为磁盘上还没有关于该结点的有用信息

B-TREE-CREATE(T)
1 x = ALLOCATE-NODE()
2 x.leaf = TRUE
3 x.n = 0
4 DISK-WRITE(x)
5 T.root = x

B-TREE-CREATE 需要 O(1) 次的磁盘操作和 O(1) 的 CPU 时间

4、向 B 树中插入一个关键字：
树中插入一个关键字要比二叉搜索树中插入一个关键字复杂得多。像二叉搜索树中一样, 要查找插入新关键字的叶结点的位置。然而，在 B 树中，不能简单地创建一个新的叶结点，然后将其插入，因为这样得到的树将不再是合法的 B 树。相反，将新的关键字插入一个已经存在的叶结点上。由于不能将关键字插入一个满的叶结点，故引入一个操作, 将一个满的结点 y (有 2t - 1 个关键字) 按其中间关键字 x.key_t 分裂为两个各含 t - 1 个关键字的结点。中间关键字被提升到 y 的父结点，以标识两棵新树的划分点。但是如果 y 的父结点也是满的，就必须在插入新的关键字之前将其分裂，最终满结点的分裂会沿着树向上传播

可以在从树根到叶子这个单程向下过程中将一个新的关键字插入 B 树中。并不是等到找出插入过程中实际要分裂的满结点时才做分裂，当沿着树往下查找新的关键字所属位置时，就分裂沿途遇到的每个满结点 (包括叶结点本身)，因此，每当要分裂一个满结点 y 时，就能确保它的父结点不是满的

5、分裂 B 树中的结点：过程 B-TREE-SPLIT-CHILD 的输入是一个非满的内部结点 x (假定在主存中) 和一个使 x.c_i (也假定在主存中) 为 x 的满子结点的下标 i。这过程把这个子节点分裂成两个非满结点，并调整 x，使之包含多出来的孩子。要分裂一个满的结点，首先要让根成为一个新的空根结点的孩子, 这样才能使用 B-TREE-SPLIT-CHILD。树的高度因此增加 1；分裂是树长高的唯一途径

满结点 y = x.c_i 按照其中间关键字 S 进行分裂，S 被提升到 y 的父结点 x
在这里插入图片描述

B-TREE-SPLIT-CHILD(x, i)
1 z = ALLOCATE-NODE()
2 y = x.c
3 z.leaf = y.leaf
4 z.n = t - 1
5 for j = 1 to t - 1
6 	 z.key_j = y.key_j+t // z和y为兄弟
7 if not y.leaf
8 	 for j = 1 to t
9 		z.c_j = y.c_(j+t)
10 y.n = t - 1 // 直接删掉了
11 for j = x.n + 1 downto i + 1
12 	 x.c_j+1 = x.c_j
13 x.c_i+1 = z // 插入到x的孩子
14 for j = x.n downto i
15 	 x.key_(j+1) = x.key_j
16 x.key_i = y.key_t // 上移
17 x.n = x.n + 1
18 DISK-WRITE(y)
19 DISK-WRITE(z)
20 DISK-WRITE(x)

y 是被分裂的结点，y 是 x 的第 i 个孩子。开始时, 结点 y 有 2t 个孩子 (2t - 1 个关键字), 在分裂后减少至 t 个孩子 (t - 1 个关键字)。结点 z 取走 y 的 t 个最大的孩子 (t - 1 个关键字)，并且 z 成为 x 的新孩子, 它在 x 的孩子表中仅位于 y 之后。y 的中间关键字上升到 x 中，成为分隔 y 和 z 的关键字

第 18 ~ 20 行写出所有修改过的磁盘页面。B-TREE-SPLIT-CHILD 占用的 CPU 时间为 Θ(t)，是由第 5 ~ 6 行和第 8 ~ 9 行的循环引起的。（其他循环执行 O(t) 次迭代）这个过程执行 O(1) 次磁盘操作

6、以沿树单程下行方式向 B 树插入关键字：以沿树单程下行方式插入一个关键字 k 的操作需要 O(h) 次磁盘存取。所需的 CPU 时间为 O(h) = O(t logt(n))。过程 B-TREE-INSERT 利用 B-TREE-SPLIT-CHILD 来保证递归始终不会降至一个满结点上

B-TREE-INSERT(T, k)
1 r = T.root
// 这不是一个循环，只针对根，s为r的父结点，也为整棵树的新的根结点（1个关键字）
// 只要树不是满的，就可以调用 B-TREE-INSERT-NONFULL 插入
2 if r.n == 2t - 1
3 	s = ALLOCATE-NODE()
4 	T.root = s
5 	s.leaf = FALSE
6 	s.n = 0
7 	s.c_1 = r
8 	B-TREE-SPLIT-CHILD(s, 1)
9 	B-TREE-INSERT-NONFULL(s, k)
10 else B-TREE-INSERT-NONFULL(r, k)

对根进行分裂是增加 B 树高度的唯一途径。与二叉搜索树不同，B 树高度的增加发生在顶端而不是底部。过程通过调用 B-TREE-INSERT-NONFULL 完成将关键字 k 插入以非满的根结点为根的树中。B-TREE-INSERT-NONFULL 在需要时沿树向下递归，在必要时通过调用 B-TREE-SPLIT-CHILD 来保证任何时刻它所递归处理的结点都是非满的
在这里插入图片描述
辅助的递归过程 B-TREE-INSERT-NONFULL 将关键字插入结点 x，要求假定在调用该过程时 x 是非满的

B-TREE-INSERT-NONFULL(x, k)
1 i = x.n // 初始位置在队尾
2 if x.leaf
3 	while i ≥ 1 and k < x.key_i
4 		x.key_i+1 = x.key_i
5 		i = i - 1
6 	x.key_i+1 = k // 最终插入位置
7 	x.n = x.n + 1
8 	DISK-WRITE(x)
9 else while i ≥ 1 and k < x.key_i
10		i = i - 1
11 	 i = i + 1 // 加回去，让 key_i 刚好比K大
12 	 DISK-READ(x.c_i) // 在key_i 前面那个空挡
13 	 if x.c_i.n == 2t - 1 // 孩子结点满了，要确保分裂后有每个子树有 t个关键字
14   	B-TREE-SPLIT-CHILD(x, i) // 把孩子结点拆开
15 		if k > x.key_i
16 			i = i + 1 // 找往下递归的口子
17 		B-TREE-INSERT-NONFULL(x.c_i, k)

第 3 ~ 8 行处理 x 是叶结点的情况，将关键字 k 插入 x。如果 x 不是叶结点，则必须将 k 插入内部结点 x 为根的子树中适当的叶结点去。这种情况，9 ~ 11 行决定向 x 的哪个子结点递归下降。第 13 行检查是否是递归降至一个满子结点上，若是，则第 14 行用 B-TREE-SPLIT-CHILD 将该子结点分裂为两个非满的孩子，第 15 ~ 16 行确定向两个孩子中的哪个下降是正确的。第 13 ~ 16 行保证该程序始终不会降至一个满结点上。然后第 17 行递归地将 k 插入合适的子树中

B-TREE-INSERT 要做 O(h) 次磁盘存取，因为在每次调用 B-TREE-INSERT-NONFULL 之间，只做了 O(1) 次 DISK-READ 和 DISK-WRITE 操作。所占用的总 CPU 时间为 O(h) = O(t logt(n))
在这里插入图片描述

7、如何在一棵 B 树中找到最小关键字，以及如何找到某一给定关键字的前驱

B-TREE-FIND-MIN(x)
    if x == NIL           // T is empty
        return NIL
    else if x.leaf        // x is leaf
        return x.key[1]   // return the minimum key of x，从1开始
    else
        DISK-READ(x.c[1]) // 往下探
        return B-TREE-FIND-MIN(x.c[1])

B-TREE-FIND-MAX(x)        // 跟找最小是对称的
    if x == NIL           // T is empty
        return NIL
    else if x.leaf        // x is leaf
        return x.[x.n]    // return the maximum key of x
    else
        DISK-READ(x.c[x.n + 1])
        return B-TREE-FIND-MIN(x.c[x.n + 1])

B-TREE-FIND-PREDECESSOR(x, i)
    if !x.leaf
        DISK-READ(x.c[i]) // 右子树最大值
        return B-TREE-FIND-MAX(x.c[i])
    else if i > 1      // x is a leaf and i > 1
        return x.key[i - 1] // 前面那个元素
    else
        z = x            // 是右子节点但是是节点中第一个元素
        while true
            if z.p == NIL    // z is root
                return NIL   // z.key[i] is the minimum key in T; no predecessor
              y = z.p        // 找靠左父元素，从目标结点的父结点开始找
              j = 1
              DISK-READ(y.c[1])
              while y.c[j] != x
                  j = j + 1
                  DISK-READ(y.c[j])
              if j == 1
                  z = y // 往上找
              else
                  return y.key[j - 1]

8、假设关键字 {1, 2, …, n} 被插入一棵最小度数为 2 的空 B 树中，那么最终的 B 树有多少个结点
每次插入的键都比现有的键大，形成右脊（在树的最右边，从根结点到叶结点的一条路径），有 h+1 个结点（根结点高度为0），除了右脊上的点，其他结点都是分裂的结果，每次分裂产生两个子节点 N=h+1 (右脊) + h（其他结点数）

9、由于叶节点不需要指向子节点的指针，它们可以使用比内部节点更大的 t 值以适应相同的磁盘页面大小。展示如何修改创建和插入 B 树的过程以处理这种变化
可以通过以下方法修改插入过程：在 B-TREE-INSERT 中，检查节点是否是叶节点，如果是，则仅在其中存储的键数量是预期的两倍时才分裂它。此外，如果一个元素需要插入到已满的叶节点中，我们将叶节点分裂成两个独立的叶节点，每个叶节点中都没有存储过多的键

10、假设磁盘每允许我们任意选择磁盘页面的大小，但该取磁盘页面的时间是 a + bt, 其中 a 和 b 为规定的常数，t 为确定磁盘页大小后的 B 树的最小度数。请描述如何选择 t 以 (近似地) 最小化 B 树的查找时间
在这里插入图片描述

3、从 B 树中删除关键字

1、B 树上的删除操作与插入操作类似，只是略微复杂一点，因为可以从任意一个结点中删除一个关键字，而不仅仅是叶结点，而且当从一个内部结点删除一个关键字时，还要重新安排这个结点的孩子

必须保证一个结点不会在删除期间变得太小（根结点除外, 因为它允许有比最少关键字数 t-1 还少的关键字个数）

与简单插入法类似，当删除关键字时，一个简单删除算法，当要删除关键字的路径上结点（非根）有最少关键字个数时，也可能需要向上回溯

2、过程 B-TREE-DELETE 从以 x 为根的子树中删除关键字 k。必须保证无论何时，结点 x 递归调用自身时，x 中关键字个数至少为最小度数 t。这个条件要求比通常 B 树中的最少关键字个数多一个以上，使得有时在递归下降至子节点之前，需要把一个关键字移到子节点中。这个加强的条件允许在一趟下过程中, 就可以将一个关键字从树中删除, 无需任何向上回溯 (有一个例外)。如果根结点 x 成为一个不含任何关键字的内部结点，那么 x 就要被删除，x 的唯一孩子 x.c1 成为树的新根, 从而树的高度降低 1，同时也维持树根结点必须包含一个关键字的性质 (除非树为空)

3、从 B 树中删除关键字的各种情况
1）如果关键字 k 在结点 x 中，并且 x 是叶结点，则从 x 中删除 k

2）如果关键字 k 在结点 x 中，并且 x 是内部结点，则做以下操作:
a. 如果位于 x 的子树 y 中的结点个数至少包含 t 个关键字（多一个），则找出 k 在 y 为根的子树的前驱 k’。递归地删除 k’，并在 x 中替换 k。 (找到 k’ 并删除它可在沿树下降的单过程中完成)

b. 对称地，如果 y 有少于 t 个关键字，则检查结点 x 中后于 k 的子节点 z。如果 z 至少有 t 个关键字，则找出 k 在以 z 为根的子树中的后继 k’。递归地删除 k’，并在 x 中用 k’ 替换 k。 (找到 k’ 并删除它可在沿树下降的单过程中完成)

c. 否则, 如果 y 和 z 都只有 t - 1 个关键字，则将 k 和 z 的全部合并进 y。这样 x 就失去了 k 和指向 z 的指针，并且 y 现在包含 2t - 1 个关键字，然后释放 z 并递归地从 y 中删除 k

3）如果关键字 k 当前不在内部结点 x 中，则确定必包含 k 的子树中的根 x.c_i（如果 k 确实在树中）。如果 x.ci 有 t - 1 个关键字，则必须执行步骤 3a 或步骤 3b 或来保证降至一个至少含 t 个关键字的结点。然后通过对 x 的某个合适的子结点进行递归而结束
a. 如果 x.c_i 只有 t - 1 个关键字，但是它的一个相邻的兄弟至少包含 t 个关键字，则将 x 中的某一个关键字降至 c_i 中，将 c_i 的相邻左兄弟或右兄弟的一个关键字升至 x，将该兄弟中相应的孩子指针转移到 c_i 中，这样就使得 x.c_i 增加了一个额外的关键字

b. 如果 x.c_i 以及 x.c_i 的所有相邻兄弟只包含 t - 1 个关键字，则将 x.c_i 与一个兄弟合并，即将 x 的一个关键字移至新合并的结点，使之成为该结点中的间关键字

在这里插入图片描述

由于一棵 B 树的中大部分关键字都在叶结点中，可以预期在实际中，删除操作很经常用于从叶结点中删除关键字。这样 B-TREE-DELETE 过程只要沿树下降一趟即可，不需要向上回溯。要删除某个内部结点的关键字时，该过程也要沿树下降一趟。但可能还要返回删除了关键字的那个结点，用以其前驱或后继来取代被删除的关键字（情况 2a 和情况 2b）

一棵高度为 h 的 B 树，它只需要 O(h) 次磁盘操作，因为在递归调用该过程之间，仅需 O(1) 次对 DISK-READ 和 DISK-WRITE 的调用。所需 CPU 时间为 O(th) = O(t logt(n))

依次从图中删除 C, P 和 V 后的结果
在这里插入图片描述
delete C

delete P

delete V

4、B-TREE-DELETE 的伪代码

B-TREE-DELETE(T, x, k)
    if x 是叶节点 then
        删除 x 中的 k
    else
        找到 k 在 x 中的位置 i
        if x 的第 i 个子节点 y 至少有 t 个键 then
            k' = y 中的前驱
            用 k' 替换 k
            递归地调用 B-TREE-DELETE(T, y, k')
        else if x 的第 i+1 个子节点 z 至少有 t 个键 then
            k' = z 中的后继
            用 k' 替换 k
            递归地调用 B-TREE-DELETE(T, z, k')
        else
            将 k 和 z 合并到 y 中
            删除 x 中的 k
            递归地调用 B-TREE-DELETE(T, y, k)
    if x 是根节点 and x 没有键 then
        T.root = x 的第一个子节点
    修复 B 树的性质

修复 B 树的性质
    if x 的子节点 c 有少于 t 个键 then
        if c 的相邻兄弟节点有至少 t 个键 then
            从相邻兄弟节点借一个键
            将 x 中的一个键下降到 c
            将相邻兄弟节点中的一个键提升到 x
        else
            将 c 与一个相邻兄弟节点合并
            将 x 中的一个键下降到新合并的节点中

1）叶节点删除：如果要删除的键在一个叶节点中，直接删除该键。

2）内部节点删除：

找到要删除的键在节点中的位置 i。
检查该键的两个子节点：
如果前驱子节点（左子节点）至少有 t 个键，找到前驱键，用前驱键替换要删除的键，然后递归地删除前驱键
如果后继子节点（右子节点）至少有 t 个键，找到后继键，用后继键替换要删除的键，然后递归地删除后继键
如果两个子节点都少于 t 个键，将要删除的键与其右子节点合并到左子节点，然后递归地删除合并后的子节点中的键

3）根节点特殊处理：如果删除后根节点没有键，将根节点设为其第一个子节点

4）修复 B 树性质：如果一个子节点少于 t 个键，从相邻兄弟节点借一个键，或者与相邻兄弟节点合并