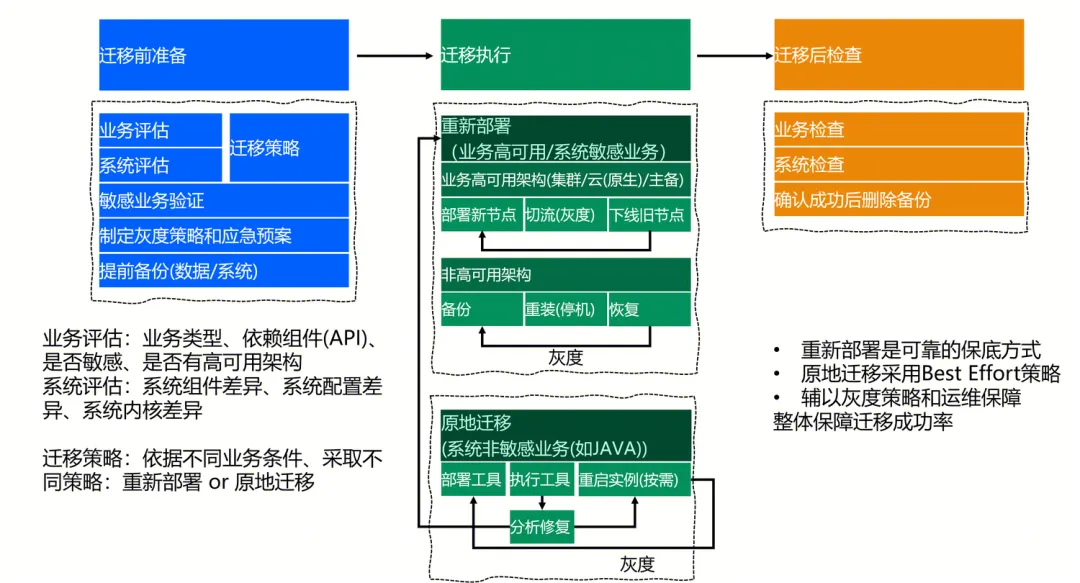
---

蒙特卡洛树搜索是一种聪明的算法，用来帮助电脑做出好的决策，尤其是在玩游戏或者解决复杂问题时。它的工作原理可以分成四个步骤：选择、扩展、模拟和反向传播。

1. 选择（Selection）

首先，想象你在一个迷宫里。选择阶段就像是从迷宫的入口开始，沿着某些路径走，直到你不能再走为止。在这一步，我们使用一些策略来决定走哪条路径，通常是选择那些看起来更有希望的路径。

在选择阶段，算法从根节点开始，根据某种策略选择一个子节点，一直到达一个叶节点。我们通常使用上置信限上界（Upper Confidence Bound, UCB）公式：

$$\text{UCB}=\frac{w_i}{n_i}+c\sqrt{\frac{\ln N}{n_i}}$$

其中：

• $w_i$ 是节点 $i$ 的赢的次数。
• $n_i$ 是节点 $i$ 的访问次数。
• $N$ 是父节点的访问次数。
• $c$ 是探索参数，通常取 $\sqrt{2}$。

2. 扩展（Expansion）

当你走到一个不能再走的地方时，你会尝试从这里开辟一条新的路径。这一步就是扩展阶段。它让我们从当前的位置开始，探索新的可能性。

3. 模拟（Simulation）

在模拟阶段，假设你继续沿着新开的路径走，直到走出迷宫或者走到尽头。在这里，我们进行很多次随机的尝试，看看每条新路径能走多远。

4. 反向传播（Backpropagation）

最后，反向传播阶段就像是回顾你刚才走过的所有路径，并记下每条路径的好坏。这样，你可以更新你走过的每个位置的信息，知道哪些路径更可能成功。

为什么蒙特卡洛树搜索很厉害？

• 探索和利用：MCTS在选择路径时，不仅会考虑那些已经看起来很好的路径（利用），还会探索那些还不太清楚的路径（探索），确保不会错过潜在的好路径。
• 渐进优化：随着尝试次数的增加，MCTS的决策会越来越好，最终接近最佳解。
• 灵活应用：MCTS不需要特别的知识，适用于各种不同的问题和游戏。

应用实例

蒙特卡洛树搜索被广泛应用于像围棋、国际象棋这样复杂的游戏中，因为它能够帮助电脑快速找到接近最佳的下棋策略。此外，它也被用在机器人控制和其他需要决策的地方。

蒙特卡洛树搜索介绍

在人工智能中，人们用博弈树来表示一个游戏，博弈树的每个节点都代表一个状态，其下一个节点的集合构成了状态的子节点。

比如，任意一个棋盘局面就是一个状态。

比如，任意一个棋盘局面就是一个状态，该局面下，所有可能落子的情况形成的新局面集合，构成了该状态的子节点。

如果是比较简单的游戏，完全可以穷举所有的状态，然后通过穷举的结果得到最优解。事实上却无法这么做，拿围棋来说，状态树比可观测宇宙中的原子数还要多，没有计算机可以做这样的穷举。

根据大数定理，当采样数量足够大，采样样本可以无限近似地表示原分布。蒙特卡洛树搜索就是这样一种，用随机采样来作为近似估计的方法。

它通过大量自博弈来寻找“最有可能走”的节点，自博弈是指让计算机模拟两个选手，从当前棋盘局面，开始用随机或简单策略开始博弈的方法。

蒙特卡洛树搜索需要定义一个策略，来选择当前局面下“最有可能走的”子节点。展开这个子节点，然后基于这个子节点完成一次自博弈。最后记录自博弈结果并更新相关数据，重复这个过程，知道满足停止条件。

那这个选择策略该如何定义？可以只看胜率吗？
不行，因为很可能节点尽管不好，但随机走子的时候赢了一盘，博弈的次数小的时候胜率并不置信，为了解决这个问题，人们定义了一个叫UCT的公式。

• $Q_i$是i节点赢的次数
• $N_i$是i节点的访问次数
• C 是常数，用来调节博弈的次数所占的权重
• T，总访问次数
  公式中加号前的部分是胜率（$\frac{Q_i}{N_i}$），后面部分的曲线如下图所示

随着访问次数的增加，值越来越小。因此，UCT更倾向于选择那些还没怎么被统计过的节点，避免了胜率高而置信度低的问题。不停的重复这个自博弈的过程，每次都选择UCT值最高的那个节点，进行自博弈，重复多次之后，访问次数最高的那个节点就是最佳节点。

这就是蒙特卡洛树搜索的全部过程。我们可以根据需要，设置蒙特卡洛树搜索的停止条件，比如10秒之后，再比如，100万次自博弈之后，自博弈次数越多，算法的表现就会越发优秀。当然，如果自博弈次数能接近于无穷大，那么我们也能得到最优解。