2.线性回归

news2025/1/6 20:30:59

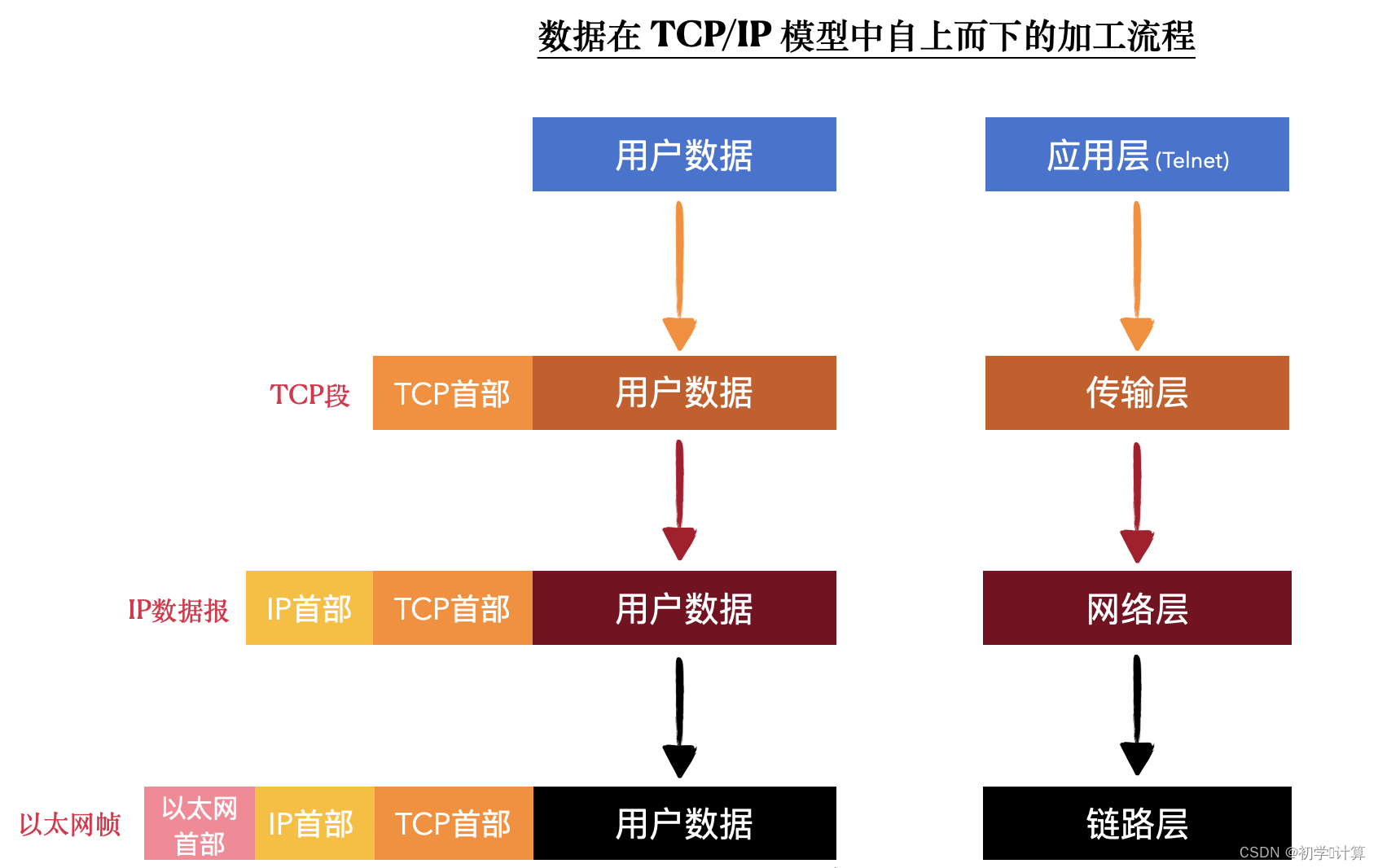
简化的房价模型

假设1：影响房价的关键因素时卧室个数，卫生间和居住面积，记为 $x_1,x_2,x_3$

假设2：成交价时关键因素的加权和：
$y = w_1x_1+w_2x_2+w_3x_3+b$
权重和偏差的实际值在后面决定

范数

$L_p范数：||x||_p =(\sum^n _{i=1}|x_i|^p)^{\frac 1p}\\$

常用的有 $L_1$ 范数和 $L_2$ 范数

L1 范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”（Lasso regularization）。范数作为正则项，会让模型参数θ稀疏化，既让模型参数向量里为0的元素尽量多。在支持向量机（support vector machine）学习过程中，实际是一种对于成本函数(cost function)求解最优，得出稀疏解。

L2 范数作为正则项式让模型参数尽量小，但不会为0，尽量让每个特征对预测值都有一些小的贡献，得出稠密解。
在梯度下降算法的迭代过程中，实际上是在成本函数的等高线上跳跃，并最终收敛在误差最小的点上（此处为未加正则项之前的成本误差）。而正则项的本质就是惩罚。模型在训练的过程中，如果没有遵守正则项所表达的规则，那么成本会变大，即受到了惩罚，从而往正则项所表达的规则处收敛。成本函数在这两项规则的综合作用下，正则化后的模型参数应该收敛在误差等值线与正则项等值线相切的点上。

一般的线性模型

n维输入 $x=[x_1,x_2,\cdots,x_n]^T$

线性模型有一个n维权重和一个标量偏差： $[w_1,w_2,\cdots,w_n]^T$

输出是输入的加权和 $y=w_1x_1+w_2x_2+\cdots+w_nx_n +n$

即
$y =< w, x > + b$
可以看作是单层的神经网络

在这里插入图片描述

衡量预估质量（损失函数）

比较真实值和预估值，损失函数。

例如 $y$ 是真实值， $\hat y$ 是估计值，则可以使用平方损失函数 $l(y,\hat y)=\frac 12 (y-\hat y)^2$

参数学习

将训练数据带入，损失函数展开为
$l(X,y,w,b)=\frac{1}{2n}\sum^n_{i=1}(y_i-<x_i,w>-b)^2 =\frac {1}{2n}||y-Xw-b||^2$
最小化损失来学习参数：
$w*,b* = arg\ min_{w,b} l(X,y,w,b)$

优化方法

梯度下降

挑选一个初始值 $w_0$
重复迭代参数 $t=1,2,3,\cdots$

$w_t = w_{t-1}-\alpha \frac{\partial l}{\partial w_{t-1}}$

沿梯度方向将增加损失函数值，学习率：步长的超参数，不能太小和太大，太小会导致计算太多次，太大会迈过了，在不停的振荡。

在这里插入图片描述

小批量随机梯度下降

在整个训练集上算梯度太贵，一个深度神经网络模型可能需要数分钟到数小时

我们可以随机采样b个样本 $i_1,i_2,\cdots,i_b$ 来近似损失
$\frac{1}{b}\sum_{i\in I_b} l(x_i,y_i,w)$
b是批量的大小，另一个重要的超参数

批量大小也不能太小，每次计算量太小，不适合并行来最大利用计算资源；不能太大，内存消耗增加浪费计算，例如如果所有样本都是相同的。

小批量梯度下降是深度学习默认的求解算法。

pytorch实现线性回归

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nn


def load_array(data_arrays, batch_size, is_train=True):
    """构建一个PyTorch数据迭代器,随机挑选b个元素，is_train表明是随机的"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset=dataset, batch_size=batch_size, shuffle=is_train)


true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)  # 根据输入的两个参数w，b生成1000个随机数据

batch_size = 10
data_iter = load_array((features, labels), batch_size, is_train=False)

# print(next(iter(data_iter)))

net = nn.Sequential(nn.Linear(2, 1))  # sequential是将层分为list of layers，可以通过下标来访问不同的层
# Linear指使用神经网络的线性层模型，输入有两个参数，输出有一个参数

net[0].weight.data.normal_(mean=0, std=0.01)  # 将第一层的layer中的参数w设置为(0,0.01)的正态分布
net[0].bias.data.fill_(0)  # 将偏差b设置为0

'''均方误差MSEloss'''
loss = nn.MSELoss()
'''SGD随机梯度下降'''
trainer = torch.optim.SGD(net.parameters(), lr=0.03)  # 传入神经网络的所有参数，学习率为0.03

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y)
        trainer.zero_grad()#梯度清零
        l.backward()#计算梯度
        trainer.step()#更新模型
    l = loss(net(features), labels)
    print(f'epoch: {epoch+1}, loss: {l:f}')