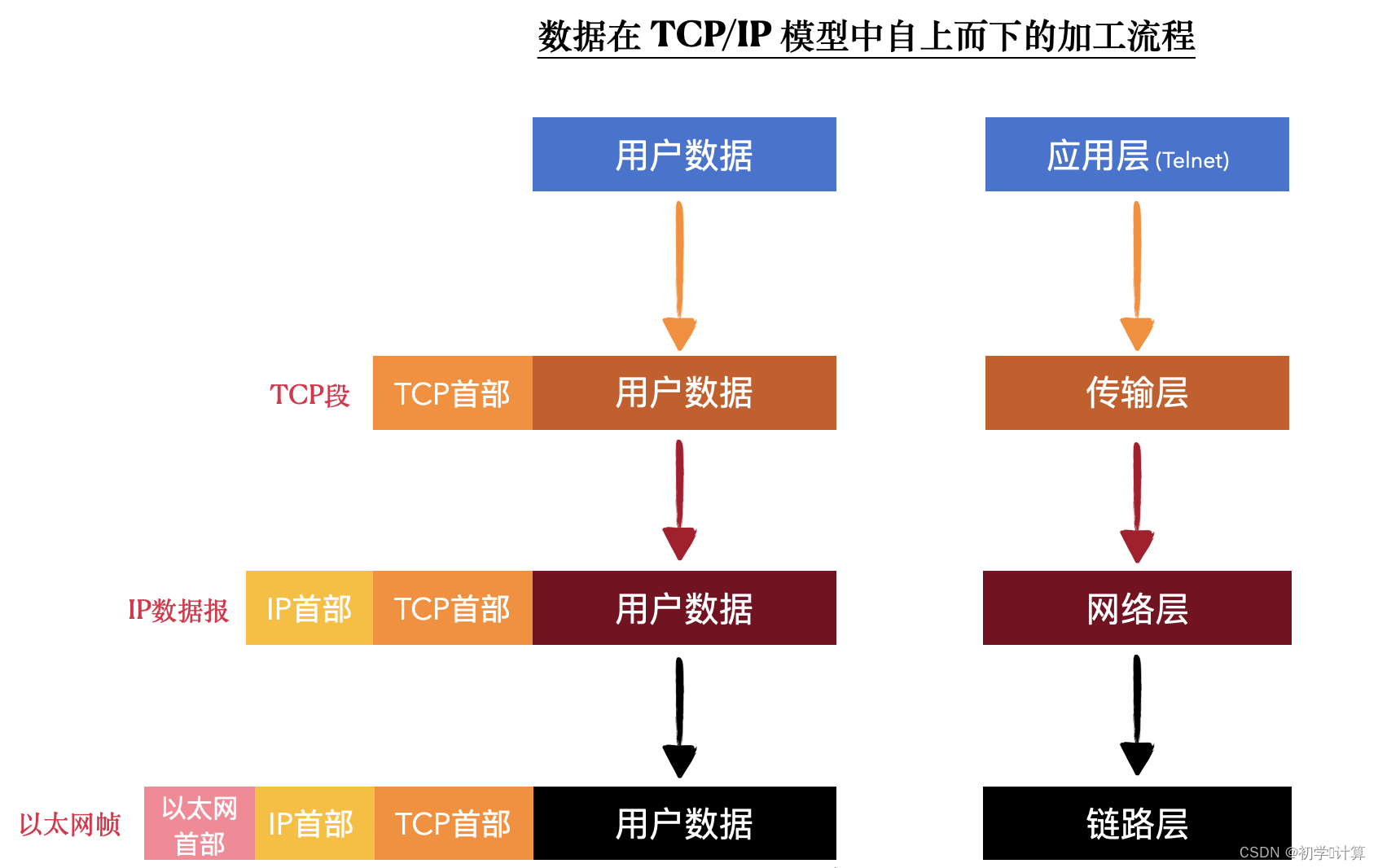
密钥证明介绍及算法规格
HUKS为密钥提供合法性证明能力,主要应用于非对称密钥的公钥的证明。
基于PKI证书链技术,HUKS可以为存储在HUKS中的非对称密钥对的公钥签发证书,证明其公钥的合法性。业务可以通过系统提供的根CA证书,逐级验证HUKS签发的密钥证明证书,来确保证书中的公钥以及对应的私钥,确实来自合法的硬件设备,且存储管理在HUKS中。同时,输出的密钥证书中包含密钥属主信息,格式如下:
| 密钥属主 | 格式 | 说明 |
|---|---|---|
| HAP应用 | {appId:“xxx”, bundleName:“xxx”} | bundleName为应用包名 |
| 系统服务 | {processName:“xxx”, APL:"system_basic | system_core"} |
说明: 当调用方为系统服务且APL等级为normal时,暂不支持密钥证明,此种情况下,processName与APL字段将置空。开发前请熟悉鸿蒙开发指导文档:
gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。
密钥证明过程如下:
- 业务将指定密钥别名和需要证明的密钥属性的标签传入HUKS。
- 调用HUKS为应用生成一个依次由根CA证书、设备CA证书、设备证书、密钥证书组成的X.509证书链。
- 将证书链传输至受信任的服务器,并在服务器上解析和验证证书链的有效性和单个证书是否吊销。
当前提供了两种密钥证明方式。
- 匿名密钥证明:不会泄露设备信息,没有权限管理。面向所有应用开放。为了保护用户设备信息,三方应用开发者只能使用匿名密钥证明。
- 非匿名密钥证明:可以看到调用方设备信息,有权限管控,需申请"ohos.permission.ATTEST_KEY"权限。

支持的算法
以下为密钥证明支持的规格说明。
面向OpenHarmony的厂商适配密钥管理服务规格分为必选规格和可选规格。必选规格为所有厂商均支持的算法规格。而对于可选规格,厂商将基于实际情况决定是否实现,如需使用,请查阅具体厂商提供的说明,确保规格支持再使用。
建议开发者使用必选规格开发应用,可保证全平台兼容。
| 算法 | 备注 | API级别 | 是否必选规格 |
|---|---|---|---|
| RSA | 支持Padding为PSS与PKCS1_V1_5的密钥 | 8+ | 是 |
| ECC | - | 8+ | 是 |
| X25519 | 仅支持非匿名接口 | 8+ | 是 |
| SM2 | - | 8+ | 是 |










106:提取不重复的整数107:哈夫曼编码108:abb](https://i-blog.csdnimg.cn/direct/82987a255aad4d168f6f92ba8da6131c.png)

![【代码随想录】【算法训练营】【第62天】 [卡码108]冗余连接 [卡码109]冗余连接II](https://i-blog.csdnimg.cn/direct/b0dc25b819274fa2abf56a603f491f57.png)