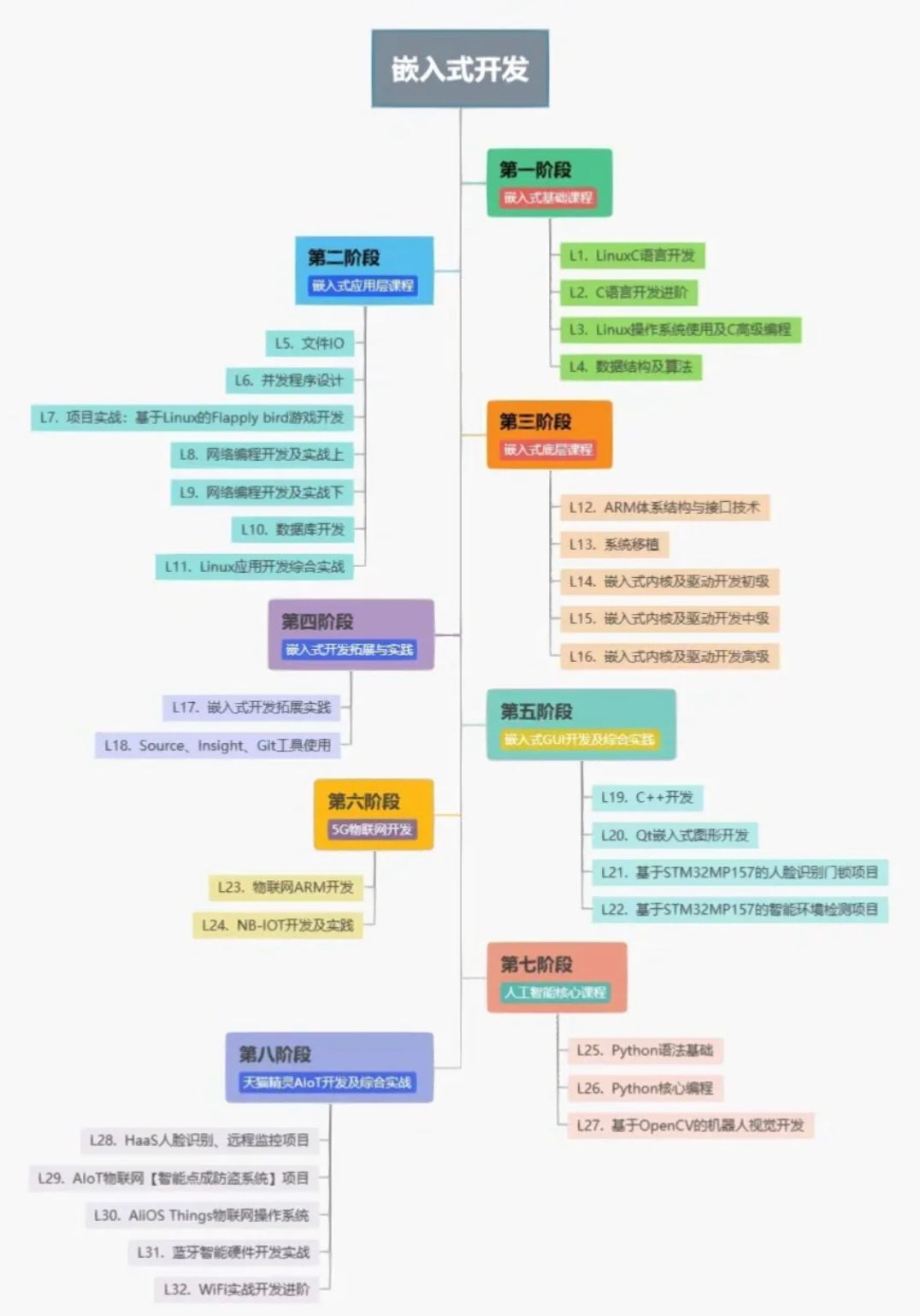
目录
- 一、数字波束形成
- 1.1 DBF原理
- 1.2 工程应用实现方式
- 1.2.1 预先存储权矢量
- 1.2.2 利用DFT/FFT实现DBF
- 二、DBF应用
- 2.1 通道间相干积累
- 2.2 测量目标角度
- 三、MATLAB代码
一、数字波束形成
数字波束形成(Digital Beam Forming,DBF) 技术,是针对阵列天线,利用阵列天线的孔径,通过数字信号处理在期望的方向形成接收波束。
DBF的物理意义:虽然单个天线的方向图是全向的,但对阵列多个接收通道的信号,利用数字处理方法,对某一方向的入射信号,补偿由于传感器在空间位置不同而引起的传播波程差导致的相位差,实现同相叠加,从而实现该方向的最大能量接收,完成该方向上的波束形成,来接收有用的期望信号,这种把阵列接收的方向增益聚集在一个指定的方向上,相当于形成了一个“波束”。
可以通过改变权值,使得波束指向不同的方向,并实现波束的扫描。通过多通道的并行处理也可以同时形成多个波束,还可以选择合适的窗函数来降低副瓣电平。
1.1 DBF原理
对于
N
N
N 个间距为
d
d
d 的阵元组成的接收阵列,考虑
p
p
p 个远场的窄带信号入射到该阵列上,假设阵元数和通道数相等,即各阵元接收到信号后经过各自的传输信道送到信号处理器,则接收信号矢量可表示为:
X
(
t
)
=
A
⋅
S
(
t
)
+
N
(
t
)
(
1
−
1
)
X(t)=A·S(t)+N(t) (1-1)
X(t)=A⋅S(t)+N(t)(1−1)
其中,
X
(
t
)
=
[
x
1
(
t
)
,
x
2
(
t
)
,
.
.
.
.
.
.
,
x
N
(
t
)
]
T
X(t)=[x_{1}(t),x_{2}(t),......,x_{N}(t)]^T
X(t)=[x1(t),x2(t),......,xN(t)]T ,为
N
×
1
N×1
N×1 维阵列接收快拍信号矢量,;
S
(
t
)
=
[
s
1
(
t
)
,
s
2
(
t
)
,
.
.
.
.
.
.
,
s
p
(
t
)
]
T
S(t)=[s_{1}(t),s_{2}(t),......,s_{p}(t)]^T
S(t)=[s1(t),s2(t),......,sp(t)]T ,为
p
×
1
p×1
p×1 维信号矢量;
N
(
t
)
N(t)
N(t) 为
N
×
1
N×1
N×1 维噪声信号矢量;
A
=
[
a
(
θ
1
)
,
a
(
θ
2
)
,
.
.
.
.
.
.
,
a
(
θ
p
)
]
A=[a(θ_{1}),a(θ_{2}),......,a(θ_{p})]
A=[a(θ1),a(θ2),......,a(θp)] 为
N
×
p
N×p
N×p 维导向矢量矩阵。
第
i
i
i 个信号的导向矢量为:
a
(
θ
i
)
=
[
1
,
e
j
2
π
d
s
i
n
θ
i
/
λ
,
.
.
.
,
e
j
2
π
(
N
−
1
)
d
s
i
n
θ
i
/
λ
]
T
a(θ_{i})=[1,e^{j2πdsinθ_{i}/λ},...,e^{j2π(N-1)dsinθ_{i}/λ}]^T
a(θi)=[1,ej2πdsinθi/λ,...,ej2π(N−1)dsinθi/λ]T
在DBF过程中,假设信号的到达方向为
θ
θ
θ ,则在该方向的导向矢量为:
a
(
θ
)
=
[
1
,
e
j
2
π
d
s
i
n
θ
/
λ
,
.
.
.
,
e
j
2
π
(
N
−
1
)
d
s
i
n
θ
/
λ
]
T
a(θ)=[1,e^{j2πdsinθ/λ},...,e^{j2π(N-1)dsinθ/λ}]^T
a(θ)=[1,ej2πdsinθ/λ,...,ej2π(N−1)dsinθ/λ]T
由式(1-1)知,对于单一信号源,有
X
(
t
)
=
A
⋅
S
(
t
)
+
N
(
t
)
X(t)=A·S(t)+N(t)
X(t)=A⋅S(t)+N(t),波束形成技术与时间滤波类似,即对采样数据
X
(
t
)
X(t)
X(t) 进行加权求和,加权后的输出信号为:
y
(
t
)
=
W
H
⋅
X
(
t
)
=
W
H
⋅
a
(
θ
)
⋅
s
(
t
)
+
W
H
⋅
N
(
t
)
(
1
−
2
)
y(t)=W^{H}·X(t)=W^{H}·a(θ)·s(t)+W^{H}·N(t) (1-2)
y(t)=WH⋅X(t)=WH⋅a(θ)⋅s(t)+WH⋅N(t)(1−2)
式中,
W
=
[
W
1
,
W
2
,
,
.
.
.
,
W
N
]
T
W=[W_{1},W_{2},,...,W_{N}]^T
W=[W1,W2,,...,WN]T ,为DBF的权矢量。
当 W = a ( θ 0 ) W=a(θ_{0}) W=a(θ0) ,即对方向为 θ 0 θ_{0} θ0 的信号进行同相相加时,输出 y ( t ) y(t) y(t) 的模值最大。该过程就是利用了波束形成技术实现对方向为 θ 0 θ_{0} θ0 的选择,即空域滤波。
等距线阵空域滤波的结构如图1所示,

图1 等距线阵空域滤波结构图
对一个阵元数
N
=
16
N=16
N=16 等距线阵,阵元间距为半波长,假设波束指向分别为-30°,0°,30°,经过DBF处理后,在指定的方向形成主瓣,其余方向形成旁瓣,数字波束形成方向图如图2所示。


图2 数字波束形成方向图
由图2可看出,未加窗时,阵列的波束形成方向图的副瓣电平为-13.15dB,采用对权矢量进行加窗处理,可以降低副瓣电平,例如加泰勒窗后,副瓣电平降低为-30.06dB,但其主瓣的3dB宽度为8.2°,相比未加窗处理的主瓣展宽了1.8°。
接收天线的阵元数不同,数字波束形成方向图也有较大区别,以波束指向为0°,未加窗处理为例,取阵元数分别为
N
=
8
、
N
=
16
、
N
=
32
N=8、N=16、N=32
N=8、N=16、N=32 时,得到数字波束形成方向图如图3所示。

由图3可以看出,当阵元数成倍数增加时,其方向图的3dB宽度成倍数减小;旁瓣数量会随着阵元数的增加而增加;副瓣电平均相同。
1.2 工程应用实现方式
1.2.1 预先存储权矢量
采用公式(1-2)进行DBF处理需要
N
2
N^2
N2 次复数乘法运算,当波束扫描的角度间隔较小,即波位数量较多时,计算量是极大的,不利于实时计算。
因此实际工程应用时,要设置合理的波束扫描间隔,并充分挖掘硬件的性能(并行计算),可以通过提前计算出权矢量的数值,预先存储在文件中,在使用时进行导入即可计算。
1.2.2 利用DFT/FFT实现DBF
在不同的方向进行DBF处理时需要采用不同的权矢量,对方向
θ
θ
θ 的权矢量为:
W
(
θ
)
=
[
1
,
e
−
j
2
π
d
s
i
n
θ
/
λ
,
.
.
.
,
e
−
j
2
π
d
s
i
n
θ
(
N
−
1
)
/
λ
]
T
(
1
−
3
)
W(θ)=[1,e^{-j2πdsinθ/λ},...,e^{-j2πdsinθ(N-1)/λ}]^T(1-3)
W(θ)=[1,e−j2πdsinθ/λ,...,e−j2πdsinθ(N−1)/λ]T(1−3)
将DBF处理搜索的波位的角度按下式进行量化:
s
i
n
θ
k
=
λ
k
N
d
,
k
=
0
,
1
,
.
.
.
,
N
−
1
(
1
−
4
)
sinθ_{k}=\frac{λk}{Nd},k=0,1,...,N-1(1-4)
sinθk=Ndλk,k=0,1,...,N−1(1−4)
则得到的权矢量为
W
(
θ
k
)
W(θ_{k})
W(θk) :
W
(
θ
k
)
=
[
1
,
e
−
j
2
π
N
k
,
.
.
.
,
e
−
j
2
π
N
(
N
−
1
)
k
]
T
(
1
−
3
)
W(θ_{k})=[1,e^{-j\frac{2π}{N}k},...,e^{-j\frac{2π}{N}(N-1)k}]^T(1-3)
W(θk)=[1,e−jN2πk,...,e−jN2π(N−1)k]T(1−3)
由式(1-3)可知,DBF的权矢量
W
(
θ
k
)
W(θ_{k})
W(θk) 为离散傅里叶变换(DFT)的旋转因子
W
N
n
k
W_{N}^{nk}
WNnk ,因此可以利用DFT或者FFT实现DBF处理,同时得到N个波位的DBF结果。
采用快速傅里叶变换(FFT)可以减少DFT的计算时间复杂度,其复数乘法的运算次数为 ( N / 2 ) l o g N (N/2)logN (N/2)logN
案例:
设有32个阵元组成间距为半波长的等距线阵,同一距离单元的两个目标的方位角分别为-20°和30°,对接收信号利用128点FFT进行DBF处理,得到的结果如下:

x坐标代表角度维,每个点的角度精度为Ag_point =0.8952,仿真计算得到的目标角度为:A1=-Ag_point *(23-1)=-19.6954°,A2=Ag_point *(128-97) =27.75°。与实际设定角度存在一定范围的差异,由角度分辨率有关。
二、DBF应用
2.1 通道间相干积累
2.2 测量目标角度
三、MATLAB代码
1.DBF方向图
clc;
clear;
close all;
%% DBF方向图
N = 16;
d_lambda = 0.5;
theta = (-90:0.1:90);
% 1、不同波束指向
theta0 = -30;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta);
figure;
plot(theta,20*log10(pattern/max(pattern)),'b-');
hold on;
theta0 = 0;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta);
plot(theta,20*log10(pattern/max(pattern)),'r-.');
theta0 = 30;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta);
plot(theta,20*log10(pattern/max(pattern)),'m--');
xlabel('方位/°');ylabel('归一化方向图/dB');xlim([-90 90]);ylim([-50 0]);
legend('\theta=-30','\theta=0','\theta=30');
title(['阵元数N=',num2str(N)]);
% 2、固定波束指向时,对比加窗前后效果
theta0 = 0;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta);
figure;
plot(theta,20*log10(pattern/max(pattern)),'b-');
hold on;
select = 3;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta,select);
plot(theta,20*log10(pattern/max(pattern)),'k--');
xlabel('方位/°');ylabel('归一化方向图/dB');xlim([-90 90]);ylim([-50 0]);
legend('未加窗','加泰勒窗');
title(['阵元数N=',num2str(N)]);
% 3、固定波束指向时,对比不同阵元数的波束形成方向图
theta0 = 0;
N = 8;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta);
figure;
plot(theta,20*log10(pattern/max(pattern)),'b-');
hold on;
N = 16;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta);
plot(theta,20*log10(pattern/max(pattern)),'r-.');
N = 32;
pattern = Antenna_Pattern(N,d_lambda,theta0,theta);
plot(theta,20*log10(pattern/max(pattern)),'k--');
xlabel('方位/°');ylabel('归一化方向图/dB');xlim([-90 90]);ylim([-50 0]);
legend('N = 8','N = 16','N = 32');
title('波束指向0度,未加窗');
2.雷达系统仿真模型
clc;
clear;
close all;
%% 雷达系统仿真模型
setParameter(); % 设置雷达系统参数
global para;
% 设置目标参数
set_TarInfo.tarNum = 2;
set_TarInfo.tar_R0 = [500,500]; % 目标距离
set_TarInfo.tar_V0 = [0,0]; % 目标速度
set_TarInfo.tar_Ag = [-20,30]; % 目标角度
set_TarInfo.Rcs = [1,5]; % 目标rcs
set_TarInfo.SNR = 10; % 信噪比
% 雷达发射和接收信号模型
para.Tx_Num = 1; % 发射阵元数目
para.Rx_Num = 32; % 接收阵元数目
global NumChirp;
NumChirp = 1;
rawData = RadarSigModel_MultiCh(set_TarInfo);
%% 雷达信号处理
global NumADC;
fs = para.fs;
u = para.u;
c = para.c;
Rx_Num = para.Rx_Num;
Nfft1 = 2^ceil(log2(NumADC)); % 距离维FFT点数
Nfft3 = 128; % 通道间FFT点数
R_point = (fs/Nfft1)*c/(2*u); % 距离点精度
Ag_point = 2/Nfft3*180/pi;
% 距离维FFT
win1 = hamming(NumADC); % 加汉明窗
fft_Data = zeros(Nfft1,Rx_Num);
for ii = 1:Rx_Num
fft_Data(:,ii) = fft(rawData(:,:,ii).*win1,Nfft1);
end
% 角度维FFT
win3 = hamming(Rx_Num); % 加汉明窗
fft3_Data = zeros(Nfft1,Nfft3);
for jj = 1:Nfft1
fft3_Data(jj,:) = fft(fft_Data(jj,:).*win3',Nfft3);
end
figure;
mesh(mag2db(abs(fft3_Data)));xlabel('角度维');ylabel('距离维');