前置二维空间的各种变换笔记:二维变换
三维空间中的齐次坐标
- 从二维变换开始引申,可得到三维中的一个点的表达方式为 ( x , y , z , 1 ) ⊤ (\mathbf{x}, \mathbf{y}, \mathbf{z}, 1)^{\top} (x,y,z,1)⊤,也就是w=1,而三维的向量则表达为 ( x , y , z , 0 ) ⊤ (\mathbf{x}, \mathbf{y}, \mathbf{z}, 0)^{\top} (x,y,z,0)⊤,也就是w=0
- 由于三维空间的一个点是上述格式的,若其中的w由于两点相加或者其他原因超过了1,则我们令这个点的xyz都除以w,那么w就会变成1了,也就是xyz所表达的位置坐标为 ( x / w , y / w , z / w ) (x / w, y / w, z / w) (x/w,y/w,z/w)
- 而在三维空间中的齐次变换矩阵则如 ( x ′ y ′ z ′ 1 ) = ( a b c t x d e f t y g h i t z 0 0 0 1 ) ⋅ ( x y z 1 ) \left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{lllc} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right) x′y′z′1 = adg0beh0cfi0txtytz1 ⋅ xyz1 所示
- 其中矩阵的abcdefghi表达为线性变换,tx、ty、tz表达为平移变换,总体表达为一种仿射变换。
- 同样,矩阵的最后一行也是(0, 0, 0, 1)
- 其中线性变换和平移变换的执行顺序是先执行线性变换,再执行平移变换,具体可以从我们二维仿射变换公式看 ( x ′ y ′ ) = ( a b c d ) ⋅ ( x y ) + ( t x t y ) \binom{x^{\prime}}{y^{\prime}}=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \cdot\binom{x}{y}+\binom{t_x}{t_y} (y′x′)=(acbd)⋅(yx)+(tytx),先乘线性变换矩阵,再加平移变换。
三维齐次变换
- 由二维向外引申,便可得到三维的各种变换矩阵形式
- 缩放变换: S ( s x , s y , s z ) = ( s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ) \mathbf{S}\left(s_x, s_y, s_z\right)=\left(\begin{array}{cccc} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) S(sx,sy,sz)= sx0000sy0000sz00001
- 平移变换: T ( t x , t y , t z ) = ( 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ) \mathbf{T}\left(t_x, t_y, t_z\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{array}\right) T(tx,ty,tz)= 100001000010txtytz1
- 旋转变换:
- 绕x轴旋转: R x ( α ) = ( 1 0 0 0 0 cos α − sin α 0 0 sin α cos α 0 0 0 0 1 ) \mathbf{R}_x(\alpha)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Rx(α)= 10000cosαsinα00−sinαcosα00001
- 绕y轴旋转: R y ( α ) = ( cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ) \mathbf{R}_y(\alpha)=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Ry(α)= cosα0−sinα00100sinα0cosα00001
- 绕z轴旋转: R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ) \mathbf{R}_z(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Rz(α)= cosαsinα00−sinαcosα0000100001
- 上述旋转都是简单的绕轴旋转,但是如果是一般性的旋转又该怎么处理呢?
- 图形学有一个大佬,就写了一个矩阵,可以把任意一个轴的旋转写成一个矩阵,这个旋转公式就是著名的Rodrigues旋转公式,公式为 R ( n , α ) = cos ( α ) I + ( 1 − cos ( α ) ) n n T + sin ( α ) ( 0 − n z n y n z 0 − n x − n y n x 0 ) ⏟ N \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^T+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{array}\right)}_{\mathbf{N}} R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)N 0nz−ny−nz0nxny−nx0
- 其中n代表要绕着的旋转轴向量
图形变换
-
模型变换:类比于在一个场景中,模型的摆放,也就是拍照时所拍的物体放在哪
-
视图变换:类比于,找到一个相机的角度,也就是相机在哪里拍照
-
投影变换: 从模型和视图变换之后做一个3d到2d的投影,类似与相机和拍摄物体都确定好了,拍照的这么个过程
视图变换如何做?
-
也就是怎么定义一个相机视角
-
首先需要相机的位置 e ⃗ \vec{e} e,其次还需要相机的朝向 g ^ \hat{g} g^,也就是往哪看,最后需要一个向上方向 t ^ \hat{t} t^来定义相机是往上看还是往下看。至此,即可确定一个相机的视角了。
-
由于只要能保住相机和其所拍摄的物体所有的相对位置都是固定的,那么无论相机和这个物体被怎样移动,那么最后拍摄下来的照片应该都是一样的才对,所以为了方便运算,有一个约定俗成的规定,就是将相机永远摆放至原点
-
假设当前相机视角如图所示,应该怎样将其变换到原点出呢
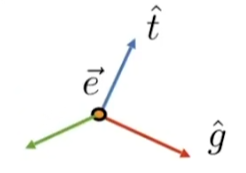
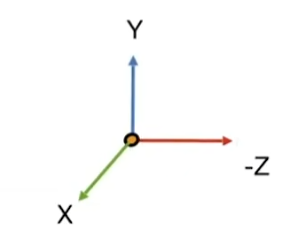
- 首先做一个平移变换将相机移动到原点
- 再将相机朝向 g ^ \hat{g} g^做旋转变换移动到-Z上
- 最后将向上朝向 t ⃗ \vec{t} t移动到Y上,那么 g × t g \times t g×t也就自动朝向X了
- 我们可以定义整个变换矩阵为M,也就是用M来表达刚刚的所有操作,那么就有 M view = R view T view M_{\text {view }}=R_{\text {view }} T_{\text {view }} Mview =Rview Tview
- 也就是先乘平移变换再乘旋转变换即可得到总的M变换矩阵,而这个变换矩阵T很好写,为 T view = [ 1 0 0 − x e 0 1 0 − y e 0 0 1 − z e 0 0 0 1 ] T_{\text {view }}=\left[\begin{array}{cccc} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{array}\right] Tview = 100001000010−xe−ye−ze1 ,也就是将自己的所在点各减去自己点离原点的距离即可
- 而旋转R矩阵则相对较难,很难直观的知道怎样从一个轴变换到X、Y、-Z轴上,但是我们如果反过来思考,如果要把X、Y、-Z轴变换到某一个轴上,就很简单了,这就是前文提到的逆变换,而我们知道,逆变换矩阵是一个正交矩阵,而正交矩阵有一个性质就是他的逆是他自己的转置 R − θ = R θ T \mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^T R−θ=RθT,于是我们只需要求出X、Y、Z如何变换到 g × t g\times t g×t、 t t t和 − g -g −g上,再对该矩阵转置一下,就能得到从 g × t g\times t g×t、 t t t和 g g g变换到X、Y、-Z的变换矩阵了。
- 比如要将X轴 [ 1 0 0 0 ] \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} 1000 旋转到 g × t g \times t g×t轴 [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 ] \begin{bmatrix} x_{\hat{g} \times \hat{t} }\\ y_{\hat{g} \times \hat{t} }\\ z_{\hat{g} \times \hat{t} }\\ 0 \end{bmatrix} xg^×t^yg^×t^zg^×t^0 上,则旋转矩阵为 [ x g ^ × t ^ 0 0 0 y g ^ × t ^ 0 0 0 z g ^ × t ^ 0 0 0 0 0 0 1 ] \left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & 0 & 0 & 0 \\ y_{\hat{g} \times \hat{t}} & 0 & 0 & 0 \\ z_{\hat{g} \times \hat{t}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] xg^×t^yg^×t^zg^×t^0000000000001 ,同理可得Y、Z轴,将其合并一下,即可得到总的逆旋转矩阵 R v i e w − 1 = [ x g ^ × t ^ x t x − g 0 y g ^ × t ^ y t y − g 0 z g ^ × t ^ z t z − g 0 0 0 0 1 ] R_{view}^{-1}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & x_t & x_{-g} & 0 \\ y_{\hat{g} \times \hat{t}} & y_t & y_{-g} & 0 \\ z_{\hat{g} \times \hat{t}} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] Rview−1= xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g00001 ,则转置后的旋转矩阵为 R v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t y t z t 0 x − g y − g z − g 0 0 0 0 1 ] R_{view}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] Rview= xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001 ,这便得到了从任意轴旋转到原点X、Y、-Z轴的旋转矩阵了,再和前面的平移矩阵T相乘,即可得到最终的变换矩阵M。
-
也就是,只要相机和所拍摄关联到的物体都按照这个M矩阵进行变换,那么在变换前和变换后所拍摄到的内容应该都是一样的。
投影变换如何做?
-
正交投影:投影前后无透视扭曲,即无近大远小的特性
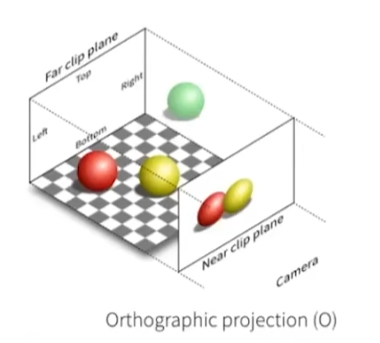
-
而想要将三维物体在无透视变化的情况下投影到二维平面上其实很简单,只需要去除这个物体的z轴就行了
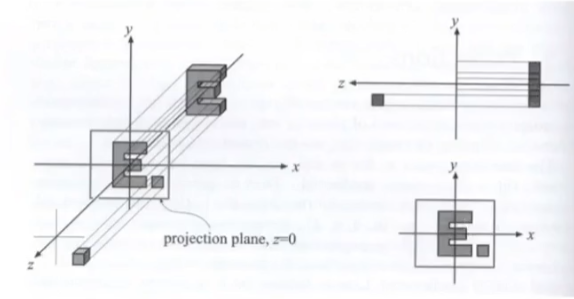
-
假设我们要投影的物体如上所示,可以发现,只要将他俩的z轴去掉,那么剩下的x,y自然就是他在二维平面上的投影。
-
但是一般情况下,需要先将这个物体通过变换矩阵转移到原点xy轴的-1到1之间的矩形之中,这样做的目的是为了简化后续操作,也就是大家都遵守这套规范,后续api啊各方面的开发就会很简便。
-
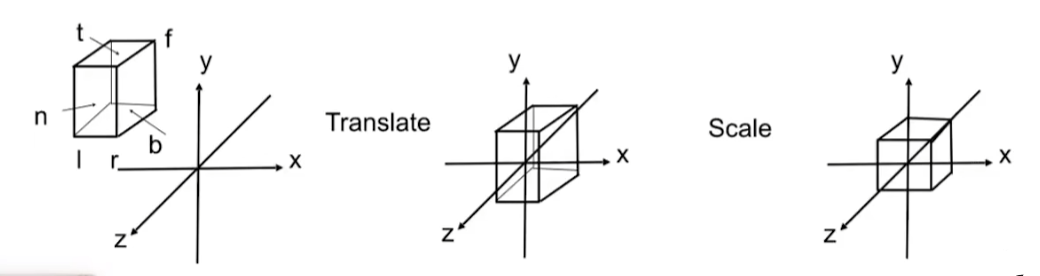
但是这样做就会出现一个问题,就是物体的前后信息丢失了,你无法显示出物体的深度信息,为了解决这个问题,通常会保留下这个z轴,也就是说先将物体通过各种变换转移到原点处xyz都在-1到1的一个立方体中,这个立方体也叫做标准化空间,这样的话物体之间的深度信息就会保留下来,也就是x和y坐标会被用来确定物体在屏幕上的位置,而z坐标则用于深度测试等目的。而最终的三维到二维的投影呢则是对这个标准化空间里做一个切片,z坐标被用来进行深度测试和裁剪,而x和y坐标则被用来确定最终在屏幕上的位置。也就是如下图所示。
-
其中l、r为物体的左右(left、right),b、t为下上(bottom、top),f、n为远近(far,near)。
-
而将被拍摄物体通过变换矩阵到原点的-1到1的空间内也就很简单了,先平移变换,再缩放变换即可(对应着上图的二图和三图)。
-
平移变换可以直接将物体的中心处移动到原点处即可,而物体的中心计算方法就很简单,x轴的中心就是 r + l 2 \frac{r+l}{2} 2r+l,yz轴同理,那么将物体最终移动到中心就是自身每个轴减去这个值即可,于是平移变换矩阵为 [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] \left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] 100001000010−2r+l−2t+b−2n+f1
-
而缩放变换呢就是要将物体规范化到-1到1的空间内,-1到1的长度为2,那么x轴的缩放就是用2除以物体的宽度,也就是 2 r − l \frac{2}{r-l} r−l2(具体数学推理就是求一个线性变换y=ax+b,将x等于l和r代入即可得到a和b的值,其中a就是缩放因子,b就是平移因子,最后解的a就是这个2/(r-l)),其他轴同理,于是缩放矩阵为 [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] \left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] r−l20000t−b20000n−f200001
-
而最终的正交投影变换矩阵为他俩相乘 M ortho = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] = [ 2 r − l 0 0 − r + l 2 0 2 t − b 0 − t + b 2 0 0 2 n − f − n + f 2 0 0 0 1 ] M_{\text {ortho }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{2} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{2} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] Mortho = r−l20000t−b20000n−f200001 100001000010−2r+l−2t+b−2n+f1 = r−l20000t−b20000n−f20−2r+l−2t+b−2n+f1
-
最后通过这个矩阵M就可以将任意物体规范化到原点处-1到1的标准空间中啦~
-
-
透视投影:有近大远小的特性
-
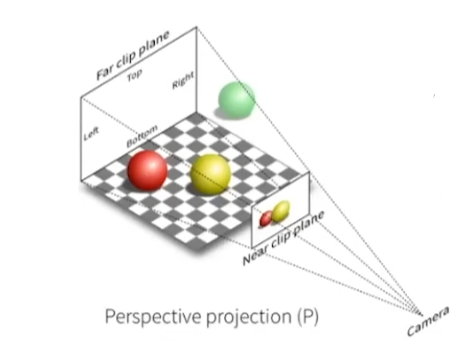
将三维物体通过透视投影到二维平面上有一个办法,由于透视投影他可以理解成沿着一个点,向外延申出四条线,如上图,那么所包裹住的物体就是一个四棱台,而我们知道,正交投影所包裹住的是一个长方体,那我们就可以先将这个四棱台压成长方体,再按照正交投影的办法去变换即可。
-
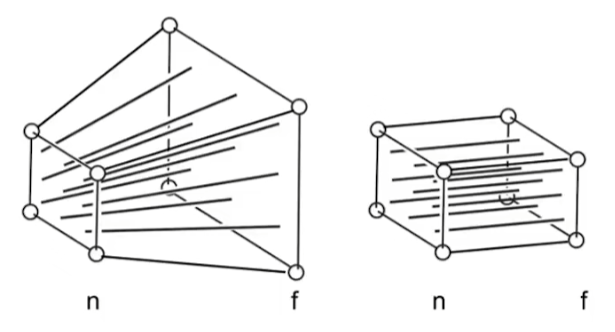
也就是将上面左图的远平面在xy轴处压成近平面的矩形,最终呈现右图的样子。显然,在这个变化当中,近平面的x、y、z都不会发生改变,而远平面的z和远平面中心点也不会发生改变。
-
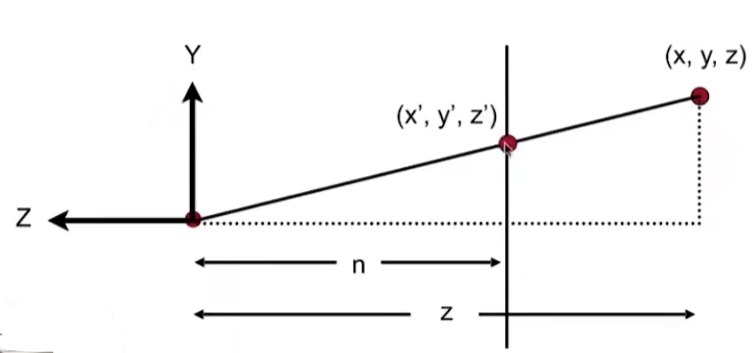
如上图所示((x’,y’,z’)是近平面的点,(x,y,z)是远平面的点),根据相似三角形原则,若点(x,y,z)想变换到点(x’,y’,z’)上,y和y’的比值一定等于n和z的比值,于是可得 y ′ = n z y y^{\prime}=\frac{n}{z} y y′=zny,同理可得 x ′ = n x y x^{\prime}=\frac{n}{x} y x′=xny
-
也就是说原本(x,y,z,1)和一个矩阵相乘后,会得到(nx/z,ny/z,不知道,1)这样的向量,而我们知道,在齐次坐标中,一个点同乘任何非0常数,所表达的矩阵依然一致,也就是(nx/z,ny/z,不知道,1)和(nx,ny,不知道,z)他俩所表达的点都是(x,y,z),也就是 M persp → ortho ( 4 × 4 ) ( x y z 1 ) = ( n x n y unknown z ) M_{\text {persp } \rightarrow \text { ortho }}^{(4 \times 4)}\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ \text { unknown } \\ z \end{array}\right) Mpersp → ortho (4×4) xyz1 = nxny unknown z
-
很容易就能得到这个M矩阵为 M persp ortho = ( n 0 0 0 0 n 0 0 ? ? ? ? 0 0 1 0 ) M_{\text {persp ortho }}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{array}\right) Mpersp ortho = n0?00n?000?100?0
-
而上述矩阵中的第三行的值可以通过前面所说的两个条件来计算,就是“近平面的x、y、z都不会发生改变,而远平面的z和远平面中心点也不会发生改变。”
-
设近平面的z轴值为n,也就是上面的M矩阵乘上近平面的(x,y,n,1)后仍然是(x,y,n,1),然后在这个齐次坐标同乘一个n,也就是 M persp → ortho ( 4 × 4 ) = ( x y n 1 ) = = ( n x n y n 2 n ) M_{\text {persp } \rightarrow \text { ortho }}^{(4 \times 4)}=\left(\begin{array}{l} x \\ y \\ n \\ 1 \end{array}\right)==\left(\begin{array}{c} n x \\ n y \\ n^2 \\ n \end{array}\right) Mpersp → ortho (4×4)= xyn1 == nxnyn2n
-
那么此时我们将M矩阵的第三行当个向量提取出来,也就是 ( 0 0 A B ) ( x y n 1 ) = n 2 \left(\begin{array}{llll} 0 & 0 & A & B \end{array}\right)\left(\begin{array}{l} x \\ y \\ n \\ 1 \end{array}\right)=n^2 (00AB) xyn1 =n2,前面两个数之所以为0是因为很明显最后的这个 n 2 n^2 n2肯定和xy无关,相乘后也就是 A n + B = n 2 A n+B=n^2 An+B=n2。
-
而远平面的中心点在变换中不会发生改变,设远平面的z轴值为f,而远平面中心点则表示为 ( 0 0 f 1 ) \left(\begin{array}{l} 0 \\ 0 \\ f \\ 1 \end{array}\right) 00f1 ,同时乘个f,则为 ( 0 0 f 2 f ) \left(\begin{array}{c} 0 \\ 0 \\ f^2 \\ f \end{array}\right) 00f2f ,和前面的 ( 0 0 A B ) \left(\begin{array}{llll} 0 & 0 & A & B \end{array}\right) (00AB)相乘后也就是 A f + B = f 2 A f+B=f^2 Af+B=f2,解两式可得 A = n + f B = − n f \begin{aligned} & A=n+f \\ & B=-n f \end{aligned} A=n+fB=−nf
-
这样就得到了最终的变换矩阵 M persp ortho = ( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) M_{\text {persp ortho }}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right) Mpersp ortho = n0000n0000n+f100−nf0 ,这个矩阵可以将任意物体从透视投影的四棱台挤压成正交投影的正方形
-
最后再按照正交投影的方法来完成后续步骤即可完成透视投影 M persp = M ortho M persp → ortho M_{\text {persp }}=M_{\text {ortho }} M_{\text {persp } \rightarrow \text { ortho }} Mpersp =Mortho Mpersp → ortho
-