在最初的二分查找中，我们将一组数据按大小排序，然后根据arr[mid]与要查找的k的大小比较，从而每次去掉一半的数字，使时间复杂度简化为O（logN）。

排序本质上是让数据的单调性统一，变为单增或单减，而不是混合的。

下面我们看一道好题：

寻找峰值_牛客题霸_牛客网

 

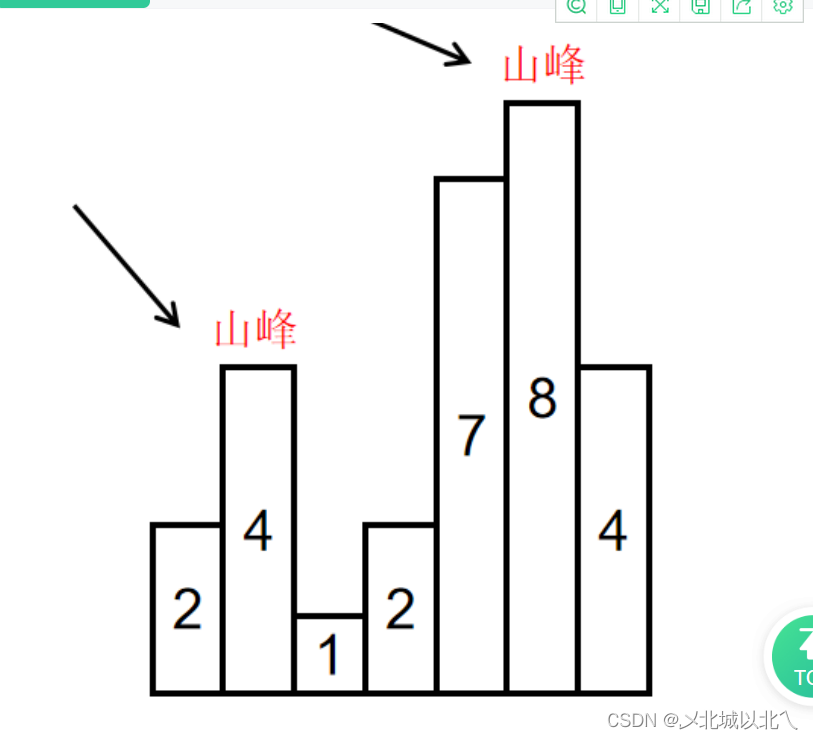
找出两个山峰，山峰是一个比两边都大的数字，也就是这组数据的极大值（极值点是坐标）

   //处理两个边界
    if(numsLen==1||nums[0]>nums[1])
    {
        return 0;
    }
    if(nums[numsLen-1]>nums[numsLen-2])
    {
        return numsLen-1;
    }

数据的首尾比较好判断，且题目中规定越界的部分为负无穷，我们可以先将这两部分判断好。

确保首尾均不是极值后，我们可以得到下图。

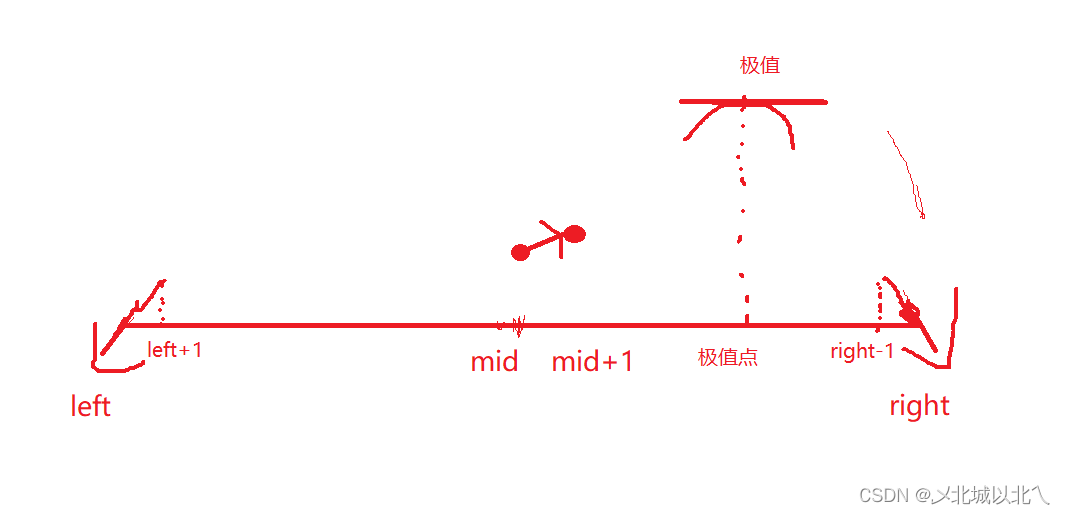
两边向下的箭头：代表靠近首尾边界时，均为单调递减 。即left<left+1对应的值，right<right-1对应的值。

然后我们对中间的值与其附近的值进行比较。这里我假设arr[mid]<arr[mid+1]，则中间向右位置是单调递增的，而右边部分可以近似理解为连续的函数（实际上是数列），一开始单增，导数>0,最后单减，导数<0，则其中必定有导数=0的极值点，因此我们就可以确定mid向右部分一定存在峰值

然而，对于左半边的部分，起始和终止均为单增，单调性一致，无法确定是否存在峰值。

int findPeakElement(int* nums, int numsLen )
{
    //处理两个边界
    if(numsLen==1||nums[0]>nums[1])
    {
        return 0;
    }
    if(nums[numsLen-1]>nums[numsLen-2])
    {
        return numsLen-1;
    }
    int i=0;
    int left=0;
    int right=numsLen-1;
    int mid=0;
    while(left<right)
    {
        mid=(right-left)/2+left;
        if(nums[mid]<nums[mid+1])
        {
            left=mid+1;
        }
        else
        {
            right=mid;
        }
      
    }
    mid=(right-left)/2+left;
    return mid;
}

left=mid+1，因为mid不可能是峰值。right=mid，因为此时mid可能是峰值。

二分查找的时间复杂度为O(logN)，是一种高效的查找方式，在做相关题目，要注意找到单调性的规律，满足什么条件时单调性改变，产生极值，是解题的关键，找到单调性的规律后，就可以一次排查掉一半数据了，还有就是注意left<right开闭区间等情况即可。