本文致力于阐述AdaBoost基本步骤涉及的每一个公式和公式为什么这么设计。
AdaBoost集成学习算法基本上遵从Boosting集成学习思想,通过不断迭代更新训练样本集的样本权重分布获得一组性能互补的弱学习器,然后通过加权投票等方式将这些弱学习器集成起来得到性能较优的集成模型。
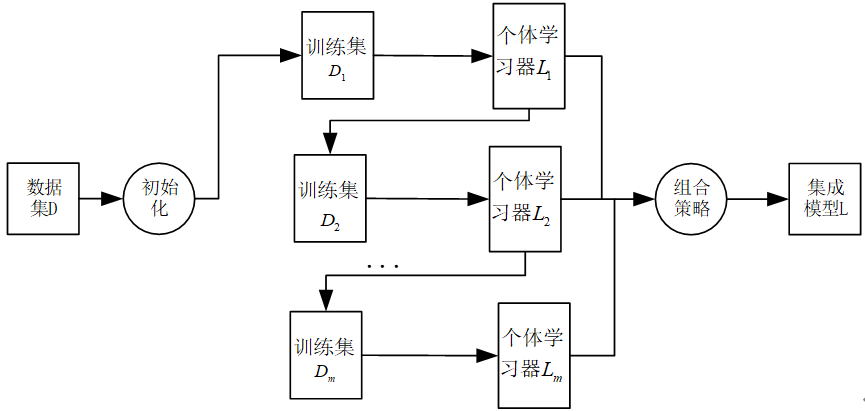
图1:Boosting集成算法思想。
下面以二分类任务(标签不是为-1,就是为+1)为例介绍该算法的具体过程。值得注意的是,下面的公式推导是以二分类任务下得出来,所以公式(比如样本权重更新公式)才会显得比较整洁,但如果换成其他任务,如多分类,那么公式会复杂很多。
对于训练样本集
D
=
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
…
,
(
x
n
,
y
n
)
D={\left(x_1,y_1\right),\left(x_2,y_2\right),\ldots,(x_n,y_n)}
D=(x1,y1),(x2,y2),…,(xn,yn),其中标签
y
i
∈
{
−
1
,
+
1
}
y_i\in\left\{-1,+1\right\}
yi∈{−1,+1},由AdaBoost集成学习算法构造集成模型的基本步骤如下:
(1)令
i
=
1
i=1
i=1并设定弱学习器的数目m。对应第一次迭代,使用均匀分布初始化训练样本集的权重分布,令
n
n
n维向量
w
i
\mathbf{w}^i
wi表示第
i
i
i次需更新的样本权重,则有:
w
1
=
(
w
11
,
w
12
,
…
,
w
1
n
)
T
=
(
1
n
,
1
n
,
…
,
1
n
)
T
\mathbf{w}^1=\left(w_{11},w_{12},\ldots,w_{1n}\right)^T=\left(\frac{1}{n},\frac{1}{n},\ldots,\frac{1}{n}\right)^T
w1=(w11,w12,…,w1n)T=(n1,n1,…,n1)T
(2)使用权重分布为
w
i
\mathbf{w}^i
wi,此时
i
=
1
i=1
i=1的训练样本集
D
i
D_i
Di学习得到第
i
i
i个弱学习器
L
i
L_i
Li;
(3)计算
L
i
L_i
Li在训练样本集
D
i
D_i
Di上的分类错误率
e
i
e_i
ei:
e
i
=
∑
k
=
1
n
w
i
k
I
(
L
i
(
X
k
)
≠
y
k
)
e_i=\sum_{k=1}^{n}{w_{ik}I \left(L_i\left(X_k\right)\neq y_k\right) }
ei=∑k=1nwikI(Li(Xk)=yk)
(4)确定弱学习器
L
i
L_i
Li的组合权重
α
i
\alpha_i
αi(
α
i
\alpha_i
αi在最后得到最终的集成模型上用到)。由于弱学习器
L
i
L_i
Li的权重取值应与其分类性能相关,对于分类错误率
e
i
e_i
ei越小的
L
i
L_i
Li,则其权重
α
i
\alpha_i
αi应该越大,故有:
α
i
=
1
2
ln
1
−
e
i
e
i
=
1
2
ln
(
1
e
i
−
1
)
\alpha_i=\frac{1}{2}\text{ln}\frac{1-e_i}{e_i}=\frac{1}{2}\text{ln}(\frac{1}{e_i}-1)
αi=21lnei1−ei=21ln(ei1−1)
可能会有人会为,为什么要这么设计
α
i
\alpha_i
αi?我在下面给出了解释。
(5)(重点)依据弱学习器
L
i
L_i
Li对训练样本集
D
i
D_i
Di的分类错误率
e
i
e_i
ei更新样本权重,样本权重更新公式为:
w
i
+
1
,
j
=
w
i
j
exp
(
−
α
i
y
k
L
i
(
x
k
)
)
Z
i
w_{i+1,j}=\frac{w_{ij}\exp(-\alpha_iy_kL_i(x_k))}{Z_i}
wi+1,j=Ziwijexp(−αiykLi(xk))
其中:
Z
i
=
∑
k
=
1
n
w
i
j
exp
(
−
α
i
y
k
L
i
(
X
k
)
)
Z_i=\sum_{k=1}^{n}{w_{ij}\exp(-\alpha_iy_kL_i(X_k))}
Zi=∑k=1nwijexp(−αiykLi(Xk))
为归一化因子,保证更新后权重向量为概率分布;
对权重更新公式的解释:
回顾开头,这是一个二分类任务,所以若样本
(
x
k
,
y
k
)
(x_k,y_k)
(xk,yk)分类正确,则要不
y
k
=
L
i
(
x
k
)
=
1
y_k=L_i(x_k)=1
yk=Li(xk)=1,要不
y
k
=
L
i
(
x
k
)
=
−
1
y_k=L_i(x_k)=-1
yk=Li(xk)=−1,因此有
y
k
∗
L
i
(
x
k
)
=
1
y_k*L_i(x_k)=1
yk∗Li(xk)=1**。**若样本
(
x
k
,
y
k
)
(x_k,y_k)
(xk,yk)分类错误,则要不
y
k
=
−
1
,
L
i
(
x
k
)
=
1
y_k=-1,L_i(x_k)=1
yk=−1,Li(xk)=1,要不
y
k
=
1
,
L
i
(
x
k
)
=
−
1
y_k=1,L_i(x_k)=-1
yk=1,Li(xk)=−1,因此有
y
k
∗
L
i
(
x
k
)
=
−
1
y_k*L_i(x_k)=-1
yk∗Li(xk)=−1。
因此公式
w
i
+
1
,
j
=
w
i
j
exp
(
−
α
i
y
k
L
i
(
x
k
)
)
Z
i
w_{i+1,j}=\frac{w_{ij}\exp(-\alpha_iy_kL_i(x_k))}{Z_i}
wi+1,j=Ziwijexp(−αiykLi(xk))
可以改写
w
i
+
1
,
j
=
{
w
i
j
Z
i
exp
(
−
α
i
)
,
y
k
=
L
i
(
x
k
)
w
i
j
Z
i
exp
(
α
i
)
,
y
k
≠
L
i
(
x
k
)
w_{i+1,j}=\begin{cases} \frac{w_{ij}}{Z_i}\exp(-\alpha_i),y_k=L_i(x_k) \\\frac{w_{ij}}{Z_i}\exp(\alpha_i),y_k\ne L_i(x_k) \end{cases}
wi+1,j={Ziwijexp(−αi),yk=Li(xk)Ziwijexp(αi),yk=Li(xk)
这样,对于错误的样本会被放大
1
−
e
i
e
i
\frac{1-e_i}{e_i}
ei1−ei倍,以便在后续弱学习器构造过程得到应有的重视。
为什么是
1
−
e
i
e
i
\frac{1-e_i}{e_i}
ei1−ei倍?
w
i
+
1
,
j
,
y
k
≠
L
i
(
x
k
)
w
i
+
1
,
j
,
y
k
=
L
i
(
x
k
)
=
w
i
j
Z
i
exp
(
α
i
)
w
i
j
Z
i
exp
(
−
α
i
)
=
exp
(
α
i
)
exp
(
−
α
i
)
=
e
2
∗
α
i
=
e
2
∗
1
2
ln
1
−
e
i
e
i
=
e
ln
1
−
e
i
e
i
=
1
−
e
i
e
i
\frac{w_{i+1,j},y_k\ne L_i(x_k)}{w_{i+1,j},y_k=L_i(x_k)}=\frac{\frac{w_{ij}}{Z_i}\exp(\alpha_i)}{\frac{w_{ij}}{Z_i}\exp(-\alpha_i)} =\frac{\exp(\alpha_i)}{\exp(-\alpha_i)}=e^{2*\alpha_i}=e^{2*\frac{1}{2}\text{ln}\frac{1-e_i}{e_i}}=e^{\text{ln}\frac{1-e_i}{e_i}}=\frac{1-e_i}{e_i}
wi+1,j,yk=Li(xk)wi+1,j,yk=Li(xk)=Ziwijexp(−αi)Ziwijexp(αi)=exp(−αi)exp(αi)=e2∗αi=e2∗21lnei1−ei=elnei1−ei=ei1−ei
另外
Z
i
Z_i
Zi的作用是归一化,使得
∑
j
=
1
n
w
i
+
1
,
j
=
1
\sum_{j=1}^{n}{w_{i+1,j}}=1
∑j=1nwi+1,j=1
(6)若
i
<
m
i<m
i<m,则令
i
=
i
+
1
i=i+1
i=i+1并返回步骤(2),否则执行步骤(7);
(7)对于
m
m
m个弱分类器
L
1
,
L
2
,
…
,
L
m
L_1{,L}_2,\ldots,L_m
L1,L2,…,Lm,分别将每个
L
i
L_i
Li按权重
α
i
\alpha_i
αi进行组合:
L
=
sign
(
∑
i
=
1
m
α
i
L
i
(
X
)
)
L=\text{sign}(\sum_{i=1}^{m}{\alpha_iL_i(X)})
L=sign(∑i=1mαiLi(X))
得到并输出所求集成模型
L
L
L,算法结束。
参考资料:《机器学习及其应用》汪荣贵等编著



















