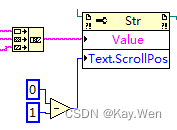
1.字符串显示控件设置自动在最下边位置
字符串属性节点中→文本→滚动条位置
滚动框在滚动条中的位置。
如需设置该位置,可连线用于表示滚动行数的数值至该属性。LabVIEW在滚动条的最后一行显示连线至该属性的数值。如需滚动至文本的最后一行,可连线行数的最大值至该属性。
如连线负数值或大于滚动条最大值的数值至该属性,滚动条将移至文本的最后一行。
图中数字类型为U32,0-1为U32最大值。
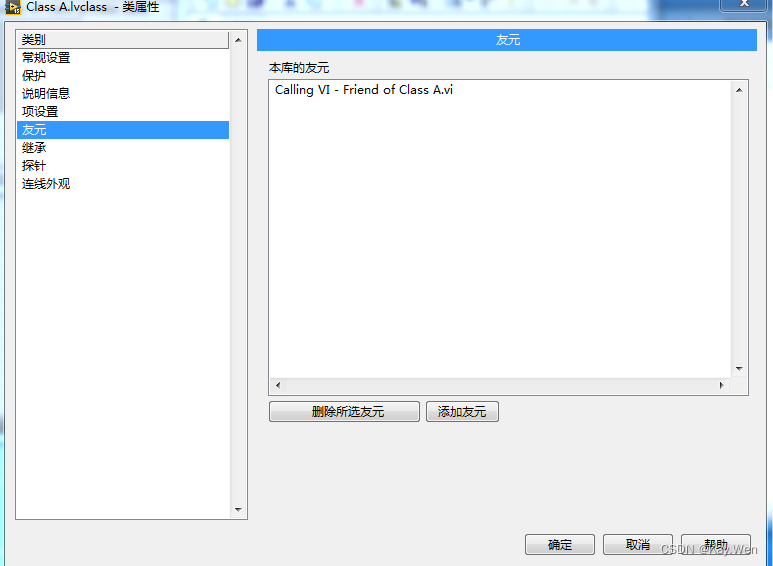
2.LabVIEW类成员的访问范围的设置
类内函数的访问范围设定:
如X.vi不是当前项目中任何一个类的成员,与其他的类也不存在友元关系
公共:X.vi可以调用该访问范围的类成员。
库内:库内,仅当前类的其他成员或该类的友元可以调用,故X.vi不可以调用该访问范围的类成员。
受保护:受保护的,仅当前类及其当前类的子孙类可以访问,故X.vi不可以调用该访问范围的类成员。
私有:私有,仅当前类的成员可以调用,故X.vi不能调用该访问范围的类成员。
其中友元的设定为在当前类右键→属性→友元
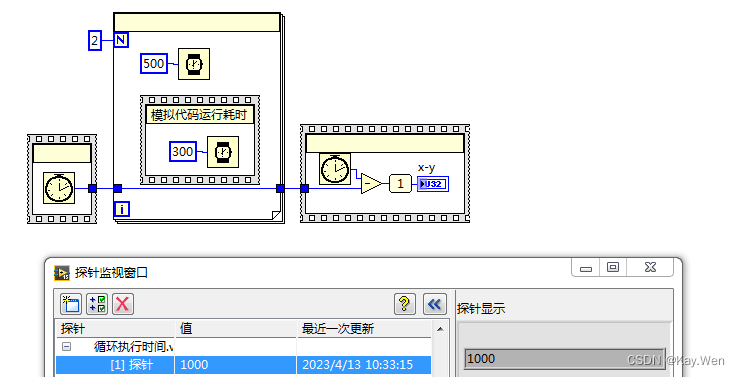
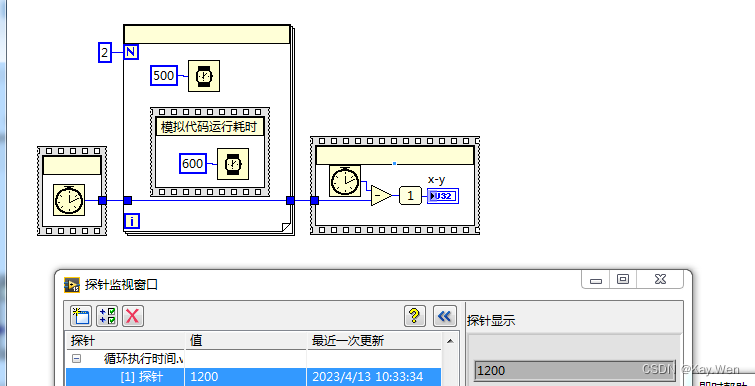
3.循环耗时
由于Labview是自动并行运行,故在循环内放置延时时,如该循环内代码的运行时间小于延时时间,则该循环运行一次的时间为延时时间。如该循环内的代码时间大于延时时间,则该循环运行一次的时间为代码执行时间。
4.副本调用问题
当主程序调用某个副本vi时,需要保证该副本vi内的所有子vi都为副本,否则该副本vi并没有起到副本vi的作用。
5.Labview调用GPIB仪器
当NI-Max无法读取到GPIB接口时需要进行如下设置,根本原因为未使用NI的GPIB卡。
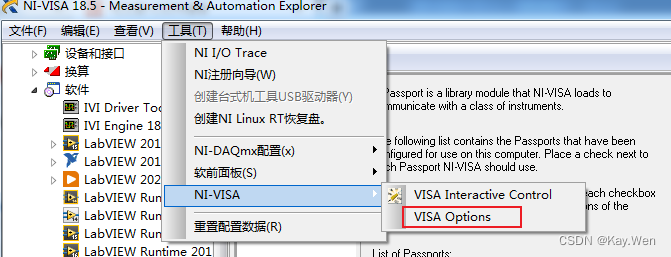
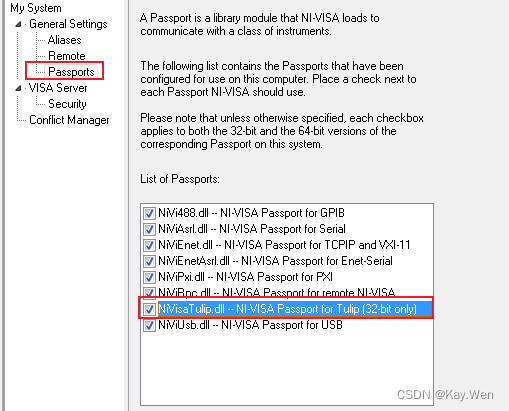
勾选NiVisaTulip.dll后再次刷新NImax。
6.集合点
集合点的底层还是使用队列的形式,以通过不超时的方式来等待多个信号的到来,达到同步执行“等待集合点”后续代码的目的。
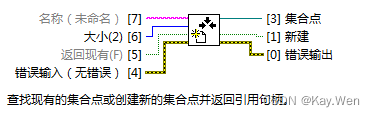
创建集合点
大小为需要等待信号的个数。
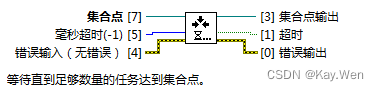
“等待集合点”只有在不超时的情况下,异步执行了多个该函数。才可以计数成功。
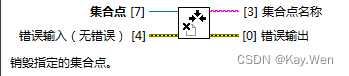
“销毁集合点” 使用完成后,销毁集合点。
7.Labview获取本地IP或者用户名
使用TCP选板中的“字符串至IP地址转换”后再使用“IP地址到字符串转换”,当后者的“句点符号”为真时,获取到的为IP地址,当当前句柄为假时获取到的为当前设备的计算机名。