第三讲 循环语句
1.偶数
编写一个程序,输出 1 到 100之间(包括 1 和 100)的全部偶数。
输入格式
无输入。
输出格式
输出全部偶数,每个偶数占一行。
输入样例
No input
输出样例
2
4
6
...
100参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
for(int i=1;i<=100;i++)
{
if(i%2==0) cout<<i<<endl;
}
return 0;
}2.奇数
输入一个整数 X,输出 1 到 X之间(包括 1 和 X)的全部奇数。
输入格式
一个整数 X。
输出格式
输出所有满足条件的奇数,每个数占一行。
数据范围
1≤X≤1000
输入样例:
8
输出样例:
1
3
5
7参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int x;
cin>>x;
for(int i=1;i<=x;i++)
{
//判断奇数是%2的结果不等于0
if(i%2!=0) cout<<i<<endl;
}
return 0;
}3.正数
输入 6个实数,它们要么是正数,要么是负数。
请你统计并输出正数的个数。
输入格式
六个数字,每个占一行。
输出格式
输出格式为 x positive numbers,其中 x 为正数的个数。
数据范围
输入数字的绝对值不超过 100。
输入样例:
7
-5
6
-3.4
4.6
12
输出样例:
4 positive numbers 参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
//因为要从0统计>=0数的个数,所以s最开始定义 = 0;
int s = 0;
for(int i=0;i<6;i++)
{
//题目描述中输入可能是浮点数,所以直接输出浮点数
float x;
cin>>x;
if(x>0) s++;
}
printf("%d positive numbers",s);
return 0;
}4.连续奇数的和1
给定两个整数 X 和 Y,输出在他们之间(不包括 X 和 Y)的所有奇数的和。
输入格式
第一行输入 X,第二行输入 Y。
输出格式
输出一个整数,表示所有满足条件的奇数的和。
数据范围
−100≤X,Y≤100
输入样例1:
6
-5
输出样例1:
5
输入样例2:
15
12
输出样例2:
13
输入样例3:
12
12
输出样例3:
0参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int x,y;
cin>>x>>y;
//由于不知道x和y谁是最大值,所以在进行求和前先判断xy的大小,若x>y则进行交换.
if(x>y)
{
int t = x;
x = y;
y = t;
}
int s = 0;
for(int i = x+1;i<y;i++)
{
if(i%2!=0) s+=i;
}
cout<<s<<endl;
return 0;
}5.最大数和它的位置
给定 100 个整数,请你找出其中最大的数字,以及它的输入位置(位置从 1 开始)。
输入格式
共 100 行,每行包含一个整数。
输出格式
第一行输出最大的数字。
第二行输出该数字的输入位置。
数据范围
1≤输入数字≤50000
保证输入数字互不相同。
输入样例:
22229
48558
24992
4755
11923
...
20213
输出样例:
48558
2参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int a,b;
for(int i=1;i<=100;i++)
{
//每次输入新的值后都进行对比是否比当前保存的最大值大,若大则更换.
int x;
cin>>x;
if(x>b)
{
a=i;
b = x;
}
}
cout<<b<<endl<<a<<endl;
return 0;
}6.递增序列
读取一系列的整数 X,对于每个 X,输出一个 1,2,…,X 的序列。
输入格式
输入文件中包含若干个整数,其中最后一个为 0,其他的均为正整数。
每个整数占一行。
对于输入的正整数,按题目要求作输出处理。
对于最后一行的整数 0,不作任何处理。
输出格式
对于每个输入的正整数 X,输出一个从 1 到 X 的递增序列,每个序列占一行。
数据范围
1≤X≤100
输入样例:
5
10
3
0
输出样例:
1 2 3 4 5
1 2 3 4 5 6 7 8 9 10
1 2 3参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
//由于当读取到零0的时候停止,所以先设计死循环while(1),当读取到0时候break while
//每次输出一行后换行,所以再for循环结束后再换行.
while(1)
{
int x;
cin>>x;
if(x==0) break;
else
{
for(int i=1;i<=x;i++)
{
cout<<i<<" ";
}
cout<<endl;
}
}
return 0;
}7.连续整数相加
读入两个整数值 A 和 N,计算从 A 开始的 N 个连续整数的和。
注意,如果读入的 N为 0 或负数,则继续读取数字直至读入 N 值为正整数为止。
输入格式
共一行,包含整数 A 和若干个整数 N(不超过 100 个)。
输出格式
一个整数,表示从 A 开始的 N 个连续整数的和。
数据范围
1≤A≤100,
−100≤N≤100
输入样例1:
3 2
输出样例1:
7
输入样例2:
3 -1 0 -2 2
输出样例2:
7参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
//因为b可能为<=0所以要一直输入知道b>0停止.
while(b<=0)
{
cin>>b;
}
int s = 0;
//相加从本身到本身后b个数(包含本身)
for(int i=0;i<b;i++)
{
s +=(a+i);
}
cout<<s<<endl;
return 0;
}8.约数
输入一个整数 N,按照从小到大的顺序输出它的全部约数。
输入格式
一个整数 N。
输出格式
输出全部约数,每个约数占一行。
数据范围
1≤N≤1000
输入样例:
6
输出样例:
1
2
3
6参考代码:
#include <cstdio>
int main()
{
int n=0;
scanf("%d",&n);
//约数就是n%i为0的数.
for(int i=1;i<=n;i++)
{
if(n%i==0) printf("%d\n",i);
}
return 0;
}9.PUM
输入两个整数 N 和 M,构造一个 N 行 M 列的数字矩阵,矩阵中的数字从第一行到最后一行,按从左到右的顺序依次为 1,2,3,…,N×M。
矩阵构造完成后,将每行的最后一个数字变为 PUM。
输出最终矩阵。
输入格式
共一行,包含两个整数 N 和 M。
输出格式
输出最终矩阵,具体形式参照输出样例。
数据范围
1≤N,M≤20
输入样例:
7 4
输出样例:
1 2 3 PUM
5 6 7 PUM
9 10 11 PUM
13 14 15 PUM
17 18 19 PUM
21 22 23 PUM
25 26 27 PUM
参考代码:
#include <cstdio>
int main()
{
int m,n;
scanf("%d %d",&m,&n);
int count=1;
//for循环中第一个for循环确定行,第二个for循环确定列
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
if(count%n==0)
{
count++;
printf("PUM\n"); //每行以pum结尾所以记得换行.
}
else
{
printf("%d ",count);
count++;
}
}
}
return 0;
}10.余数
输入一个整数 N,请按顺序输出 11到 10000之间(不包括 1 和 10000)的所有除以 N余 2 的数字。
输入格式
一个整数 N。
输出格式
输出所有满足条件的数字,从小到大每行输出一个。
数据范围
2<N<10000
输入样例:
13
输出样例:
2
15
28
41
... 参考代码:
#include <cstdio>
int main()
{
int x;
scanf("%d",&x);
for(int i=2;i<10000;i++)
{
if(i%x==2) printf("%d\n",i);
}
return 0;
}11.六个奇数
读取一个整数 X,输出 X之后的 6 个奇数,如果 X 也是奇数,那么它也算作 6个奇数之一。
输入格式
一个整数 X。
输出格式
所有满足条件的奇数,每个占一行。
数据范围
1≤X≤100
输入样例:
9
输出样例:
9
11
13
15
17
19参考代码:
#include <cstdio>
int main()
{
int x;
scanf("%d",&x);
int count=0;
//输入6个结束,所以count<6
for(int i=x;count<6;i++)
{
if(i%2!=0)
{
count++;
printf("%d\n",i);
}
}
return 0;
}12.乘法表
输入一个整数 N,输出 N的乘法表,如下:
1 x N = N
2 x N = 2N
...
10 x N = 10N
输入格式
一个整数 N。
输出格式
输出 N的乘法表,具体形式参照输出样例。
数据范围
1<N<1000
输入样例:
140
输出样例:
1 x 140 = 140
2 x 140 = 280
3 x 140 = 420
4 x 140 = 560
5 x 140 = 700
6 x 140 = 840
7 x 140 = 980
8 x 140 = 1120
9 x 140 = 1260
10 x 140 = 1400参考代码:
#include <cstdio>
int main()
{
int x;
scanf("%d",&x);
for(int i=1;i<=10;i++)
{
printf("%d x %d = %d\n",i,x,i*x);
}
return 0;
}13.实验
医学部一共进行了 N 场动物实验。
共有三种小动物可用来实验,分别是青蛙、老鼠和兔子。
每次实验都会选取其中一种动物来参与实验,选取数量若干。
现在请你统计一下医学部一共用了多少小动物,每种分别用了多少,每种动物使用数量占总量的百分比分别是多少。
输入格式
第一行包含整数 N,表示实验次数。
接下来 N 行,每行包含一个整数 A(表示一次实验使用的小动物的数量)和一个字符 T(表示一次实验使用的小动物的类型,C 表示兔子(coney),R 表示老鼠(rat),F 表示青蛙(frog))。
输出格式
请你参照输出样例,输出所用动物总数,每种动物的数量,以及每种动物所占百分比。
注意输出百分比时,保留两位小数。
数据范围
1≤N≤100,
1≤A≤15
输入样例:
10
10 C
6 R
15 F
5 C
14 R
9 C
6 R
8 F
5 C
14 R
输出样例:
Total: 92 animals
Total coneys: 29
Total rats: 40
Total frogs: 23
Percentage of coneys: 31.52 %
Percentage of rats: 43.48 %
Percentage of frogs: 25.00 %参考代码:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
int n;
int a;
char t;
int sum=0,sum1=0,sum2=0,sum3=0;//sum1表示兔子,sum2表示老鼠,sum3表示青蛙
double s1,s2,s3;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a>>t;
if(t=='C')
sum1+=a;
else if(t=='R')
sum2+=a;
else
sum3+=a;
sum+=a;
}
//(double)表示将类型强制转换为double类型.
s1=(double)sum1/(double)sum*100;
s2=(double)sum2/(double)sum*100;
s3=(double)sum3/(double)sum*100;
cout<<"Total: "<<sum<<" animals"<<endl;
cout<<"Total coneys: "<<sum1<<endl;
cout<<"Total rats: "<<sum2<<endl;
cout<<"Total frogs: "<<sum3<<endl;
printf("Percentage of coneys: %.2lf %\n",s1);
printf("Percentage of rats: %.2lf %\n",s2);
printf("Percentage of frogs: %.2lf %\n",s3);
return 0;
}
14.区间 2
读取 N 个整数 X1,X2,…,XN,判断这 N 个整数中有多少个在 [10,20] 的范围内,有多少个在范围外。
输入格式
第一行包含整数 N,表示共有 N个整数需要进行判断。
接下来 N 行,每行包含一个整数 Xi。
输出格式
第一行输出 x in,其中 x为在范围内的整数的数量。
第二行输出 y out,其中 y为在范围外的整数的数量。
数据范围
1≤N≤10000,
−10^7<Xi<10^7
输入样例:
4
14
123
10
-25
输出样例:
2 in
2 out15.连续奇数的和 2
输入 N对整数对 X,Y,对于每对 X,Y,请你求出它们之间(不包括 X 和 Y)的所有奇数的和。
输入格式
第一行输入整数 N,表示共有 N 对测试数据。
接下来 N行,每行输入一组整数 X 和 Y。
输出格式
每对 X,Y 输出一个占一行的奇数和。
数据范围
1≤N≤100,
−1000≤X,Y≤1000
输入样例:
7
4 5
13 10
6 4
3 3
3 5
3 4
3 8
输出样例:
0
11
5
0
0
0
12参考代码:
#include <iostream>
using namespace std;
int main()
{
int n;
scanf("%d",&n);
for(int i=0l;i<n;i++)
{
int x,y;
int sum=0;
scanf("%d %d",&x,&y);
//swap(x,y)交换函数,等于原来交换方法的三瓶子法.将x于y的值互换
if(x>y) swap(x,y);
for(int j=x+1;j<y;j++)
{
if(j%2!=0) sum+=j;
}
printf("%d\n",sum);
}
return 0;
}16.简单斐波那契
以下数列 0 1 1 2 3 5 8 13 21 ... 被称为斐波纳契数列。
这个数列从第 33 项开始,每一项都等于前两项之和。
输入一个整数 N,请你输出这个序列的前 N 项。
输入格式
一个整数 N。
输出格式
在一行中输出斐波那契数列的前 N 项,数字之间用空格隔开。
数据范围
0<N<46
输入样例:
5
输出样例:
0 1 1 2 3参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int main()
{
cin>>n;
//本题的斐波那契以0为第一项,1为第二项.
int a = 0,b = 1;
for(int i=0;i<n;i++)
{
printf("%d ",a);
//每次求出新的一项,a,b都往后平移
int c = a + b;
a = b, b = c;
}
return 0;
}17.数字序列和它的和
输入若干个整数对 M,N,对于每个数对,输出以这两个数为最大值和最小值的公差为 1 的等差数列。
注意,当输入整数对中,任意一个数为 0 或负整数时,立即停止输入,且该组数对无需作任何处理。
输入格式
输入共若干行,每行包含两个整数。
最后一行的两个整数中,至少有一个是非正整数。
输出格式
对于每组需作处理的数对,输出一个结果,每个结果占一行。
结果包含从最小值到最大值的数字序列以及数字序列各数字之和。
具体格式请参照输出样例。
数据范围
M,N≤100
输入样例:
2 5
6 3
5 0
输出样例:
2 3 4 5 Sum=14
3 4 5 6 Sum=18参考代码:
#include <iostream>
using namespace std;
int main()
{
int m=1,n=1;
cin>>m>>n;
while(m>0&&n>0)
{
int sum=0;
//判断mn大小,若m>n则交换使得m<n
if(m>n) swap(m,n);
//求m到n所有数的和包括m和n
for(int i=m;i<=n;i++)
{
cout<<i<<" ";
sum+=i;
}
cout<<"Sum="<<sum<<endl;
cin>>m>>n;
}
return 0;
}18.完全数
一个整数,除了本身以外的其他所有约数的和如果等于该数,那么我们就称这个整数为完全数。
例如,6 就是一个完全数,因为它的除了本身以外的其他约数的和为 1+2+3=6。
现在,给定你 N 个整数,请你依次判断这些数是否是完全数。
输入格式
第一行包含整数 N,表示共有 N个测试用例。
接下来 N 行,每行包含一个需要你进行判断的整数 X。
输出格式
每个测试用例输出一个结果,每个结果占一行。
如果测试数据是完全数,则输出 X is perfect,其中 X 是测试数据。
如果测试数据不是完全数,则输出 X is not perfect,其中 X 是测试数据。
数据范围
1≤N≤100,
1≤X≤10^8
输入样例:
3
6
5
28
输出样例:
6 is perfect
5 is not perfect
28 is perfect参考代码:
#include <iostream>
using namespace std;
int main()
{
int n=0;
cin>>n;
for(int i=0;i<n;i++)
{
//因为本题的范围最大为10的8次方所以用long long类型.
long long x=0;
cin>>x;
long long sum=0;
for(int j=1;j*j<=x;j++)
{
if(x%j==0)
{
if(j<x) sum+=j;
if(x/j!=j && x/j<x) sum+=x/j;
}
}
if(sum==x) printf("%lld is perfect\n",x);
else printf("%lld is not perfect\n",x);
}
return 0;
}19.质数
一个大于 1 的自然数,如果除了 1 和它自身外,不能被其他自然数整除则称该数为质数。
例如 7 就是一个质数,因为它只能被 1 和 7 整除。
现在,给定你 N 个大于 1 的自然数,请你依次判断这些数是否是质数。
输入格式
第一行包含整数 N,表示共有 N 个测试数据。
接下来 N行,每行包含一个自然数 X。
输出格式
每个测试用例输出一个结果,每个结果占一行。
如果测试数据是质数,则输出 X is prime,其中 X 是测试数据。
如果测试数据不是质数,则输出 X is not prime,其中 X是测试数据。
数据范围
1≤N≤100
1<X≤10^7
输入样例:
3
8
51
7
输出样例:
8 is not prime
51 is not prime
7 is prime参考代码:
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int n=0;
cin>>n;
for(int j=0;j<n;j++)
{
int x; cin>>x;
int i=0;
//i<=sqrt(x)也就是根号x,此方法更快速.
for( i=2;i<=sqrt(x);i++)
{
if(x%i==0)
{
printf("%d is not prime\n",x);
//当判断当前数为质数后就可以推出此for循环
break;
}
}
if(i>sqrt(x)) printf("%d is prime\n",x);
}
return 0;
}20.菱形
输入一个奇数 n,输出一个由 * 构成的 n阶实心菱形。
输入格式
一个奇数 n。
输出格式
输出一个由 * 构成的 n 阶实心菱形。
具体格式参照输出样例。
数据范围
1≤n≤99
输入样例:
5
输出样例:
*
***
*****
***
* 参考代码:
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int n;
cin>>n;
//本题可当作模板题,先背过
int cx=n/2,cy=n/2;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
//abs()绝对值函数,最后结果全部为正数.
if(abs(i-cx)+abs(j-cy)<=n/2) cout<<"*";
else cout <<" ";
}
cout<<endl;
}
return 0;
}第四讲 数组
1.数组替换
输入一个长度为 1010 的整数数组 X[10],将里面的非正整数全部替换为 1,输出替换完成后的数组。
输入格式
输入包含 10 个整数,每个整数占一行。
输出格式
输出新数组中的所有元素,每个元素占一行。
输出格式为 X[i] = x,其中 i为元素编号(从 0 开始),x 为元素的值。
数据范围
−100≤X[i]≤100
输入样例:
10
-9
0
-4
-10
0
-2
-7
7
4
输出样例:
X[0] = 10
X[1] = 1
X[2] = 1
X[3] = 1
X[4] = 1
X[5] = 1
X[6] = 1
X[7] = 1
X[8] = 7
X[9] = 4参考代码:
#include <iostream>
using namespace std;
int main()
{
int a[10];
for(int i=0;i<10;i++)
{
cin>>a[i];
if(a[i]<=0) a[i]=1;
printf("X[%d] = %d\n",i,a[i]);
}
return 0;
}2.数组填充
输入一个整数 V,输出一个长度为 10 的数组 N,数组中的第一个元素为 V,每个后续元素的值都为上一个元素的值的 2 倍。
例如,如果输入整数为 1,则数组为:1,2,4,8…
输入格式
输入一个整数 V。
输出格式
输出数组中的所有元素,每个元素占一行。
输出格式为 N[i] = x,其中 i 为元素编号(从 0 开始),x 为元素的值。
数据范围
1≤V≤50
输入样例:
1
输出样例:
N[0] = 1
N[1] = 2
N[2] = 4
N[3] = 8
N[4] = 16
N[5] = 32
N[6] = 64
N[7] = 128
N[8] = 256
N[9] = 512参考代码:
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int v;
cin>>v;
int a[10];
//每次输出2的i次方
for(int i=0;i<10;i++)
{
//pow(x,y)函数用来求x的y次方.
a[i]=v*pow(2,i);
printf("N[%d] = %d\n",i,a[i]);
}
return 0;
}3.数组选择
输入一个长度为 100 的数组 A,请你按顺序输出其中不大于 10的所有元素。
输入格式
输入 100 个数,每个数占一行,表示数组的所有元素的值。
每个数可能是整数也可能是浮点数。
输出格式
按顺序输出数组中的所有不大于 10 的元素,每个元素占一行。
输出格式为 A[i] = x,其中 i 为元素编号,x 为元素的值。
注意,所有的 x 均保留一位小数。
数据范围
−100≤A[i]≤100
输入样例:
0
-5
63
-8.5
...
输出样例:
A[0] = 0.0
A[1] = -5.0
A[3] = -8.5
...参考代码:
#include <iostream>
using namespace std;
int main()
{
//数组定义的时候尽量定义更多一些,防止空间不够用.
double a[110];
for(int i=0;i<100;i++)
{
cin>>a[i];
if(a[i]<=10) printf("A[%d] = %.1lf\n",i,a[i]);
}
return 0;
}
4.数组中的行
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组中某一行的元素的平均值或元素的和。
输入格式
第一行输入整数 L,表示所求的具体行数(行数从 0 开始计数)。
第二行包含一个大写字母,若为 S,则表示需要求出第 L 行的元素的和,若为 M,则表示需要求出第 L行的元素的平均值。
接下来 1212 行,每行包含 1212 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或元素的和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
7
S
8.3 -9.4 -5.6 9.9 2.2 3.2 6.9 7.7 -2.9 -6.3 3.9 -1.4
-0.5 4.3 -0.3 2.3 0.7 -3.1 -6.3 5.7 -7.7 -3.7 9.7 3.8
5.8 -9.1 3.5 7.0 2.5 -2.3 6.9 2.7 5.8 -4.6 -7.8 4.3
-1.7 -8.9 -2.6 7.5 -9.6 6.4 -4.7 -8.0 0.6 6.7 -1.8 -0.4
-9.8 8.9 -3.8 -2.1 5.8 -9.4 1.3 6.3 -1.3 -6.3 -6.6 8.8
-6.3 -7.2 -6.3 -5.9 6.2 9.3 2.0 -4.3 2.7 3.6 -4.6 8.7
3.8 7.4 8.7 -2.8 6.0 -9.2 1.9 3.1 -7.2 -6.0 9.7 -8.4
-9.8 6.6 8.6 2.3 1.1 -2.9 6.6 -1.5 2.1 -5.1 6.4 -7.5
-0.6 -1.6 9.5 -6.6 3.0 3.4 -7.5 -7.9 3.1 2.0 1.7 -7.6
-9.0 9.4 6.6 -0.2 1.4 6.5 8.6 2.0 -1.3 0.2 4.0 -2.4
-7.3 -6.3 -8.6 -7.5 8.5 1.4 -3.3 7.1 0.8 3.3 3.0 0.1
3.3 9.0 1.7 5.2 -3.7 8.9 3.8 -7.4 -2.8 0.6 -2.4 7.1
输出样例:
6.9参考代码:
#include <iostream>
using namespace std;
int main()
{
int n;
char s;
cin>>n>>s;
double a[12][12];
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
}
}
double sum=0;
//获得第n行的每列的数.
for(int i=0;i<12;i++)
{
sum+=a[n][i];
}
if(s=='M')
printf("%.1lf\n",sum/12);
else printf("%.1lf\n",sum);
return 0;
}5.数组的右上半部分
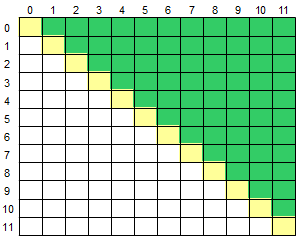
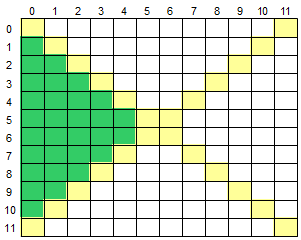
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的右上半部分元素的平均值或元素的和。
右上半部分是指主对角线上方的部分,如下图所示,黄色部分为对角线,绿色部分为右上半部分:
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出右上半部分的元素的和,若为 M,则表示需要求出右上半部分的元素的平均值。
接下来 12 行,每行包含 12 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1 行的第 j+1个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或元素的和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
M
-6.5 8.2 0.7 9.0 0.8 -4.3 0.9 -0.0 -7.9 7.1 -1.6 4.6
-9.4 -9.0 1.5 -9.0 -5.1 -0.5 -2.8 -9.1 8.0 -6.9 -5.5 -6.6
-6.8 0.3 3.8 6.1 -9.9 -9.3 8.5 8.6 5.0 6.9 -3.6 -3.0
-0.8 -1.6 -7.3 -6.7 4.4 -9.1 -9.0 1.6 0.3 -6.0 6.0 -0.8
-0.8 -6.0 -4.9 -3.9 6.4 6.2 -4.2 -0.9 7.9 1.6 -8.2 -9.2
7.8 -5.8 -5.8 -5.8 7.2 0.5 -7.9 1.2 -6.8 -9.1 0.3 -1.4
4.3 -7.2 3.5 -6.4 -9.1 -6.0 3.5 -5.1 -5.6 -6.9 -9.1 -2.1
-7.6 -7.1 0.7 -1.7 5.0 -9.0 1.4 -6.2 7.6 4.8 -7.5 4.0
-0.2 0.3 -4.2 8.4 0.7 -6.4 -2.7 3.5 -0.9 3.7 0.9 -2.7
7.1 0.1 8.4 -5.1 -7.9 -0.5 -5.3 -5.7 -4.6 9.6 -8.3 7.0
9.6 -9.8 3.3 -9.9 -6.8 6.7 3.1 1.2 -9.5 -4.3 -1.7 -9.7
1.8 5.0 8.3 -0.7 -0.9 3.2 2.5 0.5 7.3 8.3 0.3 0.9
输出样例:
-1.2参考代码:
#include <iostream>
using namespace std;
int main()
{
char s;
cin>>s;
double a[12][12];
double sum=0;
int count=0;
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
//图中所有绿色部分都是行坐标大于列坐标(i>j)
if(j>i)
{
count++;
sum+=a[i][j];
}
}
}
if(s=='M') printf("%.1lf",sum/count);
else printf("%.1lf",sum);
return 0;
}6.数组的左上半部分
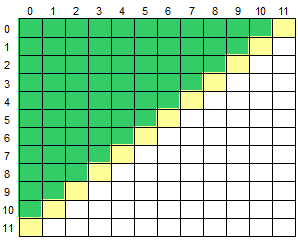
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的左上半部分元素的平均值或元素的和。
左上半部分是指次对角线上方的部分,如下图所示,黄色部分为对角线,绿色部分为左上半部分:
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出左上半部分的元素的和,若为 M,则表示需要求出左上半部分的元素的平均值。
接下来 1212 行,每行包含 1212 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
M
-0.4 -7.7 8.8 1.9 -9.1 -8.8 4.4 -8.8 0.5 -5.8 1.3 -8.0
-1.7 -4.6 -7.0 4.7 9.6 2.0 8.2 -6.4 2.2 2.3 7.3 -0.4
-8.1 4.0 -6.9 8.1 6.2 2.5 -0.2 -6.2 -1.5 9.4 -9.8 -3.5
-2.3 8.4 1.3 1.4 -7.7 1.3 -2.3 -0.1 -5.4 -7.6 2.5 -7.7
6.2 -1.5 -6.9 -3.9 -7.9 5.1 -8.8 9.0 -7.4 -3.9 -2.7 0.9
-6.8 0.8 -9.9 9.1 -3.7 -8.4 4.4 9.8 -6.3 -6.4 -3.7 2.8
-3.8 5.0 -4.6 2.0 4.0 9.2 -8.9 0.5 -3.9 6.5 -4.3 -9.9
-7.2 6.2 -1.2 4.1 -7.4 -4.6 4.7 -0.4 -2.2 -9.1 0.4 -5.8
9.1 -6.4 9.2 0.7 10.0 -5.7 -9.7 -4.4 4.7 4.7 4.9 2.1
-1.2 -6.2 -8.2 7.0 -5.3 4.9 5.5 7.2 3.4 3.2 -0.2 9.9
-6.9 -6.2 5.1 8.5 7.1 -0.8 -0.7 2.7 -6.0 4.2 -8.2 -9.8
-3.5 7.7 5.4 2.8 1.6 -1.0 6.1 7.7 -6.5 -8.3 -8.5 9.4
输出样例:
-0.8参考代码:
#include <iostream>
using namespace std;
int main()
{
char s;
cin>>s;
double a[12][12];
double sum=0;
int count=0;
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
//图中所有绿色部分行左坐标i+列坐标j的值都小于11
if(j+i<11)
{
count++;
sum+=a[i][j];
}
}
}
if(s=='M') printf("%.1lf",sum/count);
else printf("%.1lf",sum);
return 0;
}7.数组的上方区域
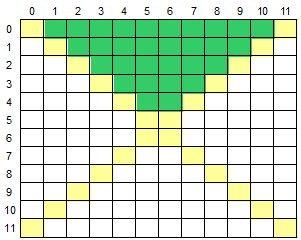
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的上方区域元素的平均值或元素的和。
数组的两条对角线将数组分为了上下左右四个部分,如下图所示,黄色部分为对角线,绿色部分为上方区域:
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出上方区域的元素的和,若为 M,则表示需要求出上方区域的元素的平均值。
接下来 12行,每行包含 12个用空格隔开的浮点数,表示这个二维数组,其中第 i+1 行的第 j+1个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或和的值,保留一位小数。
输出结果与标准答案据对误差不超过 0.1即视为正确。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
S
-4.8 -8.0 -2.9 6.7 -7.0 2.6 6.5 1.7 1.9 5.6 -1.6 -6.3
-4.3 1.5 8.7 -0.3 5.4 -9.3 4.8 7.0 3.6 -8.3 -1.0 1.3
-9.9 9.7 -6.3 5.8 2.9 2.9 -7.7 4.9 -0.6 7.2 6.4 7.7
2.8 -5.8 -0.0 2.2 4.0 7.7 -3.0 -7.5 -3.5 9.7 -4.3 -8.6
-1.8 -0.1 5.4 0.6 9.9 -3.7 -1.1 0.8 -0.2 -0.0 9.9 4.5
3.0 -3.9 2.1 -9.7 5.5 9.4 -4.6 3.3 -9.6 5.1 -4.5 1.5
4.3 -5.4 -7.9 9.2 -7.7 -9.6 -1.5 -1.6 -7.2 2.0 -3.7 -0.7
8.0 2.8 -4.1 7.1 8.4 -5.6 3.9 -9.7 -1.1 3.0 -8.5 -3.3
1.7 5.1 0.1 9.2 4.5 9.7 7.2 8.6 8.7 1.1 6.7 0.3
-3.6 -7.1 -8.9 7.1 -5.9 1.6 -7.4 6.7 3.9 4.3 -2.4 -3.7
8.9 -6.2 5.0 -8.6 -1.3 -8.8 2.6 8.9 5.5 9.0 -2.2 -4.4
5.7 3.7 1.8 -2.1 -7.3 -7.9 4.7 6.0 3.3 -2.8 1.4 -6.9
输出样例:
21.7参考代码:
#include <iostream>
using namespace std;
int main()
{
char s;
cin>>s;
double a[12][12];
double sum=0;
int count=0;
for(int i=0;i<5;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
//(i表示行,j表示列)图中所有绿色部分的列都大于行,且列小于11-行
if(j>i && j<11-i)
{
count++;
sum+=a[i][j];
}
}
}
if(s=='M') printf("%.1lf",sum/count);
else printf("%.1lf",sum);
return 0;
}8. 数组的左方区域
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的左方区域元素的平均值或元素的和。
数组的两条对角线将数组分为了上下左右四个部分,如下图所示,黄色部分为对角线,绿色部分为左方区域:
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出左方区域的元素的和,若为 M,则表示需要求出左方区域的元素的平均值。
接下来 12 行,每行包含 12个用空格隔开的浮点数,表示这个二维数组,其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
S
4.7 -3.3 -2.3 4.5 -7.0 8.7 -4.1 -3.0 -7.6 6.3 -6.6 -4.7
-7.2 9.3 -7.6 9.1 9.2 9.0 5.5 -7.5 -9.3 -1.6 -3.5 -4.2
0.5 -7.5 -8.3 -9.0 -6.4 3.8 0.1 -3.5 7.9 2.1 2.4 -6.2
7.0 5.7 -9.0 -5.8 1.6 2.6 -9.2 -6.2 4.6 8.2 -8.3 -1.4
3.8 -9.9 6.2 -2.5 -3.5 9.4 1.6 7.0 3.3 -0.5 6.7 6.0
1.6 -3.8 5.0 8.8 4.2 7.7 0.7 7.4 7.9 -5.9 4.4 3.3
3.7 6.2 6.7 -1.4 6.1 -6.0 8.5 9.1 5.7 -4.2 5.9 -3.5
5.0 0.3 2.2 -3.6 6.3 -10.0 9.5 -4.7 2.7 8.1 7.5 -8.4
-5.7 -0.3 -3.7 -3.3 7.7 9.3 -1.3 1.0 0.3 1.9 9.9 9.0
-7.4 1.3 -9.6 -3.6 2.2 3.4 -3.6 3.5 8.3 0.5 9.7 -6.8
1.0 -2.7 -1.5 5.4 -6.5 -3.7 5.6 8.0 -9.9 0.1 2.2 7.6
5.6 4.3 1.5 -0.8 5.8 -5.1 5.5 6.2 -5.8 8.8 -0.6 -2.3
输出样例:
13.3参考代码:
#include <cstdio>
int main()
{
char t;
scanf("%c", &t);
double q[12][12];
for (int i = 0; i < 12; i ++ )
for (int j = 0; j < 12; j ++ )
scanf("%lf", &q[i][j]);
double s = 0, c = 0;
//先统计1-5行绿色格子
for (int i = 1; i <= 5; i ++ )
for (int j = 0; j <= i - 1; j ++ )
{
s += q[i][j];
c += 1;
}
//再统计6-10行绿色格子
for (int i = 6; i <= 10; i ++ )
for (int j = 0; j <= 10 - i; j ++ )
{
s += q[i][j];
c += 1;
}
if (t == 'S') printf("%.1lf\n", s);
else printf("%.1lf\n", s / c);
return 0;
}
* 9.平方矩阵 I
输入整数 N,输出一个 N 阶的回字形二维数组。
数组的最外层为 1,次外层为 2,以此类推。
输入格式
输入包含多行,每行包含一个整数 N。
当输入行为 N=0 时,表示输入结束,且该行无需作任何处理。
输出格式
对于每个输入整数 N,输出一个满足要求的 N 阶二维数组。
每个数组占 N行,每行包含 N 个用空格隔开的整数。
每个数组输出完毕后,输出一个空行。
数据范围
0≤N≤100
输入样例:
1
2
3
4
5
0
输出样例:
1
1 1
1 1
1 1 1
1 2 1
1 1 1
1 1 1 1
1 2 2 1
1 2 2 1
1 1 1 1
1 1 1 1 1
1 2 2 2 1
1 2 3 2 1
1 2 2 2 1
1 1 1 1 1
参考代码:
#include <iostream>
using namespace std;
int main()
{
int n;
while(cin>>n,n)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
int up=i,down=n-i+1,left=j,right=n-j+1;
cout<<min(min(up,down),min(left,right))<<" ";
}
cout<<endl;
}
cout<<endl;
}
return 0;
}10.数组变换
输入一个长度为 20 的整数数组 N,将整个数组翻转,使得第一个元素成为倒数第一个元素,第二个元素成为倒数第二个元素,…,倒数第二个元素成为第二个元素,倒数第一个元素成为第一个元素。
输出翻转后的数组。
输入格式
输入包含 20 个整数,每个数占一行。
输出格式
输出新数组中的所有元素,每个元素占一行。
输出格式为 N[i] = x,其中 i 为元素编号(从 0 开始),x为元素的值。
数据范围
−100≤N[i]≤100
输入样例:
0
-5
...
63
23
输出样例:
N[0] = 23
N[1] = 63
...
N[18] = -5
N[19] = 0参考代码:
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int a[20];
for(int i=0;i<20;i++)
{
cin>>a[i];
}
//reverse(数组名,数组名+要求逆置的长度)逆置函数,将reverse(12345)逆置->得到 54321
reverse(a,a+20);
for(int i=0;i<20;i++)
{
printf("N[%d] = %d\n",i,a[i]);
}
return 0;
}11.斐波那契数列
输入整数 N,求出斐波那契数列中的第 N 项是多少。
斐波那契数列的第 0 项是 0,第 1 项是 1,从第 2 项开始的每一项都等于前两项之和。
输入格式
第一行包含整数 T,表示共有 T 个测试数据。
接下来 T 行,每行包含一个整数 N。
输出格式
每个测试数据输出一个结果,每个结果占一行,
结果格式为 Fib(N) = x,其中 N 为项数,x 为第 N 项的值。
数据范围
0≤N≤60
输入样例:
3
0
4
2
输出样例:
Fib(0) = 0
Fib(4) = 3
Fib(2) = 1参考代码:
#include <iostream>
using namespace std;
int main()
{
//因为怕超出int范围所以定义long long类型数组
long long a[61];
int n=0; cin>>n;
for(int i=0;i<n;i++)
{
int m; cin>>m;
a[0]=0;a[1]=1;
for(int i=2;i<=m;i++)
{
a[i]=a[i-2]+a[i-1];
}
printf("Fib(%d) = %lld\n",m,a[m]);
}
return 0;
}12. 最小数和它的位置
输入一个整数 N和一个长度为 N 的整数数组 X。
请你找到数组中最小的元素,并输出它的值和下标。
注意,如果有多个最小值,则返回下标最小的那个。
输入格式
第一行包含整数 N。
第二行包含 N个用空格隔开的整数 X[i]。
输出格式
第一行输出 Minimum value: x,其中 x为数组元素最小值。
第二行输出 Position: y,其中 y 为最小值元素的下标(下标从 0 开始计数)。
数据范围
1<N≤1000,
−1000≤X[i]≤1000
输入样例:
10
1 2 3 4 -5 6 7 8 9 10
输出样例:
Minimum value: -5
Position: 4参考代码:
#include <iostream>
using namespace std;
int main()
{
int n=0;
cin>>n;
int a[n];
int min=1001;
int index=0;
//若最小值重复,返下标最小的等同于返回数组下标最靠前的那个最小值.
for(int i=0;i<n;i++)
{
cin>>a[i];
if(min>a[i])
{
min=a[i];
index=i;
}
}
printf("Minimum value: %d\nPosition: %d",min,index);
return 0;
}
13.数组中的列
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组中某一列的元素的平均值或元素的和。
输入格式
第一行输入整数 C,表示所求的具体列数(列数从 0 开始计数)。
第二行包含一个大写字母,若为 S,则表示需要求出第 C 列的元素的和,若为 M,则表示需要求出第 C 列的元素的平均值。
接下来 12 行,每行包含 12 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1行的第 j+1 个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或元素的和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
1
S
-9.0 -2.4 -3.3 2.4 -9.7 -5.7 -5.3 6.5 -7.3 4.8 -4.1 3.9
1.6 -0.9 9.2 -7.5 1.0 -8.0 -4.1 -4.0 -0.1 -9.0 8.4 4.9
-8.2 -0.3 -5.1 -5.6 6.6 0.9 -1.0 -5.4 -2.1 -4.5 -8.7 -1.1
-4.2 6.5 -8.2 3.6 -4.6 -9.2 -1.7 6.9 -9.0 -9.8 7.7 -3.4
-8.0 5.7 4.8 0.3 -1.4 2.8 -6.3 9.3 0.3 6.3 1.5 -1.7
1.7 -0.0 9.7 -6.6 1.3 -2.0 -6.1 2.0 -7.8 -4.7 -9.1 6.0
-8.2 -1.7 9.4 -1.2 -1.0 -9.0 -7.0 -6.9 -1.6 -6.8 -6.7 1.8
4.8 1.3 -6.1 -0.6 0.5 -2.9 -6.8 1.5 5.8 3.2 0.0 7.7
6.3 1.1 4.7 7.3 7.6 5.6 0.9 9.2 1.3 -4.9 7.8 -4.9
0.5 3.5 -5.0 9.0 8.8 8.7 7.5 7.5 -9.6 -6.9 -1.6 6.9
7.8 5.6 -6.4 3.6 2.3 0.5 4.1 6.1 8.6 -9.3 2.2 -0.4
9.9 0.9 6.4 -2.8 -4.2 -7.6 0.6 9.6 3.0 0.9 5.1 4.5
输出样例:
19.3
#include <iostream>
using namespace std;
int main()
{
int n;
char s;
cin>>n>>s;
double a[12][12];
double sum=0;
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
//变输出边判断如果是第c列,则加上c列所有行的元素.
if(j==n) sum+=a[i][j];
}
}
if(s=='M') printf("%.1lf",sum/12);
else printf("%.1lf",sum);
return 0;
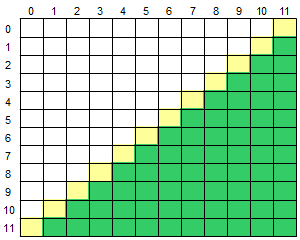
}14.数组的右下半部分
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的右下半部分元素的平均值或元素的和。
右下半部分是指次对角线下方的部分,如下图所示,黄色部分为对角线,绿色部分为右下半部分:
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出右下半部分的元素的和,若为 M,则表示需要求出右下半部分的元素的平均值。
接下来 12 行,每行包含 12 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
S
9.7 -4.9 6.1 -6.1 -9.6 1.0 -3.2 0.6 3.2 -9.8 4.9 1.2
-2.8 -5.3 2.8 -1.9 -5.4 7.5 -2.0 5.7 2.3 5.3 -7.5 8.9
6.0 4.3 3.8 -6.7 8.1 -0.5 7.8 -2.2 -1.0 4.0 -4.9 -9.4
5.4 3.7 -6.5 -3.9 -3.3 4.1 -2.5 -4.7 8.2 1.4 1.8 4.7
2.4 9.0 -4.3 9.6 8.6 -6.1 -7.4 8.6 5.6 0.5 -0.4 5.2
-5.2 2.9 -5.6 4.0 -0.2 3.8 -4.1 -1.6 -3.8 -3.1 -1.1 3.3
-9.4 -1.4 0.6 6.5 -4.3 -8.3 6.1 2.9 -5.2 2.5 9.8 -7.7
-2.9 -3.6 7.9 -5.8 -4.7 8.2 -6.2 1.0 7.4 -1.0 -4.4 -4.5
0.1 9.5 4.9 1.5 0.8 -8.2 0.4 9.5 -0.8 -0.9 9.7 -2.1
0.1 -7.6 7.8 -6.9 5.5 1.4 4.0 7.8 1.0 -1.2 9.7 -1.9
-4.6 2.3 -5.5 8.2 -4.8 -3.7 5.4 0.2 -2.4 -0.8 7.4 0.0
-0.1 8.2 0.8 -3.5 -7.6 -0.5 5.6 8.4 -8.6 0.9 9.0 -7.5
输出样例:
53.0参考代码:
#include <iostream>
using namespace std;
int main()
{
char s;
cin>>s;
double a[12][12];
double sum=0;int count=0;
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
//绿色部分所有行坐标+列坐标都>12
if(i+j>=12)
{
sum+=a[i][j];
count++;
}
}
}
if(s=='M') printf("%.1lf",sum/count);
else printf("%.1lf",sum);
return 0;
}
15.数组的左下半部分
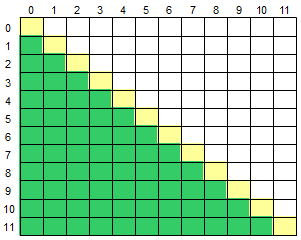
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的左下半部分元素的平均值或元素的和。
左下半部分是指主对角线下方的部分,如下图所示,黄色部分为对角线,绿色部分为左下半部分:
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出左下半部分的元素的和,若为 M,则表示需要求出左下半部分的元素的平均值。
接下来 12行,每行包含 12 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1行的第 j+1 个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
S
8.7 5.6 -2.0 -2.1 -7.9 -9.0 -6.4 1.7 2.9 -2.3 8.4 4.0
-7.3 -2.1 0.6 -9.8 9.6 5.6 -1.3 -3.8 -9.3 -8.0 -2.0 2.9
-4.9 -0.5 -5.5 -0.2 -4.4 -6.1 7.6 6.9 -8.0 6.8 9.1 -8.5
-1.3 5.5 4.6 6.6 8.1 7.9 -9.3 9.6 4.6 0.9 -3.5 -4.3
-7.0 -1.2 7.0 7.1 -5.7 7.8 -2.3 4.3 0.2 -0.4 -6.6 7.6
-3.2 -5.4 -4.7 4.7 3.6 8.8 5.1 -3.1 -2.9 2.8 -4.3 -1.4
-1.8 -3.3 -5.6 1.8 8.3 -0.5 2.0 -3.9 -1.0 -8.6 8.0 -3.3
-2.5 -9.8 9.2 -0.8 -9.4 -0.5 1.6 1.5 3.4 -0.1 7.0 -6.2
-1.0 4.9 2.2 -8.7 -0.9 4.8 2.3 2.0 -3.2 -7.5 -4.0 9.9
-1.1 -2.9 8.7 3.6 7.4 7.8 10.0 -9.0 1.6 8.3 6.3 -5.8
-9.9 0.6 2.0 -3.8 -6.3 0.6 7.3 3.8 -7.1 9.5 2.2 1.3
-2.8 -9.1 7.1 -0.2 0.6 -6.5 1.1 -0.1 -3.6 4.0 -5.4 1.1
输出样例:
-2.8参考代码:
#include <iostream>
using namespace std;
int main()
{
char s;
cin>>s;
double a[12][12];
double sum=0;int count=0;
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
//绿色部分行坐标大于列坐标
if(i>j)
{
sum+=a[i][j];
count++;
}
}
}
if(s=='M') printf("%.1lf",sum/count);
else printf("%.1lf",sum);
return 0;
}16.数组的下方区域
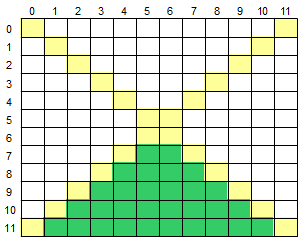
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的下方区域元素的平均值或元素的和。
数组的两条对角线将数组分为了上下左右四个部分,如下图所示,黄色部分为对角线,绿色部分为下方区域:
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出下方区域的元素的和,若为 M,则表示需要求出下方区域的元素的平均值。
接下来 12 行,每行包含 12 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1行的第 j+1个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
S
-6.0 0.7 -8.4 -5.7 -4.1 7.6 9.5 -9.7 4.1 0.6 -6.5 -4.9
6.6 4.9 -3.1 5.3 0.3 -4.5 3.9 -1.5 6.6 7.0 5.1 2.5
-8.5 1.8 -2.7 0.1 -4.9 -7.2 4.3 6.0 -1.4 2.7 -3.0 2.0
4.8 -7.0 -1.3 0.8 1.0 4.5 -1.1 -2.9 -3.9 -3.9 -8.9 5.8
-2.1 -9.6 5.1 0.2 1.0 -1.7 6.4 4.1 2.8 -6.9 2.4 9.3
-6.0 -9.1 -7.0 -7.0 7.8 5.1 6.9 -7.6 0.4 -7.2 5.5 6.0
-1.9 5.5 1.9 -8.5 -5.3 2.3 -9.3 2.0 -0.2 1.2 5.6 -1.8
8.2 2.3 3.5 1.4 4.0 -5.1 -6.9 -2.8 1.7 -7.0 7.8 1.8
-6.0 -4.1 -4.6 -9.4 -4.9 -4.1 4.2 6.3 -2.8 8.7 8.1 -0.9
8.8 -6.5 -4.3 6.1 -6.2 -3.9 -7.0 7.3 5.0 -0.9 -0.0 5.6
-2.4 1.4 8.5 -2.2 0.9 5.3 3.6 8.8 -8.1 3.0 -3.1 6.5
-3.8 -6.4 2.3 4.2 -9.8 -0.3 -9.9 -7.4 3.5 1.5 -0.2 7.0
输出样例:
-11.9参考代码:
#include <iostream>
using namespace std;
int main()
{
char s;
cin>>s;
double a[12][12];
double sum=0;int count=0;
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
}
}
//绿色部分7-11行,列起始为12-i(当前行),小于行-1;
for(int i=7;i<=11;i++)
{
for(int j=12-i;j<=i-1;j++)
{
sum+=a[i][j];
count++;
}
}
if(s=='M') printf("%.1lf",sum/count);
else printf("%.1lf",sum);
return 0;
}17.数组的右方区域
输入一个二维数组 M[12][12],根据输入的要求,求出二维数组的右方区域元素的平均值或元素的和。
数组的两条对角线将数组分为了上下左右四个部分,如下图所示,黄色部分为对角线,绿色部分为右方区域:
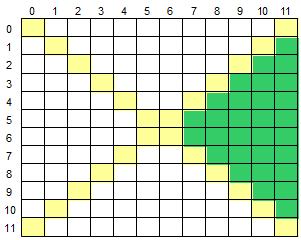
输入格式
第一行输入一个大写字母,若为 S,则表示需要求出右方区域的元素的和,若为 M,则表示需要求出右方区域的元素的平均值。
接下来 12行,每行包含 12 个用空格隔开的浮点数,表示这个二维数组,其中第 i+1行的第 j+1个数表示数组元素 M[i][j]。
输出格式
输出一个数,表示所求的平均数或和的值,保留一位小数。
数据范围
−100.0≤M[i][j]≤100.0
输入样例:
S
2.4 7.8 9.4 -5.6 6.9 -4.9 4.8 0.8 3.6 1.7 -1.4 9.7
-6.8 -3.7 -2.0 -4.9 -4.5 -5.3 6.1 7.5 -4.3 5.9 -9.5 9.7
-6.5 -0.4 1.6 3.7 -4.4 -3.3 1.9 7.7 -1.4 4.5 7.4 -3.0
-1.2 0.4 9.8 9.8 -4.3 -1.3 -1.6 0.5 2.8 -4.0 8.5 3.9
0.2 -2.0 -6.4 -9.8 3.7 -2.0 1.7 -3.6 -3.4 2.4 -1.2 -3.9
-8.3 5.8 -1.0 -4.4 1.0 -2.4 2.8 -4.6 2.1 8.7 -6.8 -8.3
6.3 -6.8 -7.0 9.3 -7.7 -1.7 8.2 -6.5 -1.8 6.7 8.2 4.4
0.4 8.6 -1.2 8.6 -4.6 1.8 9.6 1.6 2.0 -1.0 3.9 -9.2
7.5 -3.1 6.2 -4.5 -3.0 2.5 -7.7 2.9 0.3 3.3 -2.7 3.4
-5.0 3.0 -0.0 4.3 9.5 -0.0 -9.9 -8.6 -0.9 -5.5 7.7 6.5
4.9 -9.6 -2.9 8.5 2.0 -9.9 -4.9 -1.5 -2.4 -7.6 1.7 8.5
-6.4 6.8 -3.7 -4.7 0.2 5.8 -5.4 0.6 7.0 -4.2 -7.5 -2.4
输出样例:
40.9参考代码:
#include <iostream>
using namespace std;
int main()
{
char s;cin>>s;
double a[12][12];
for(int i=0;i<12;i++)
{
for(int j=0;j<12;j++)
{
cin>>a[i][j];
}
}
double sum=0; int count=0;
//统计前五行,每行起始12-行数,小于等于11
for(int i=1;i<=5;i++)
{
for(int j=12-i;j<=11;j++)
{
sum+=a[i][j];
count++;
}
}
//统计后五行,每行起始行数+1,小于等于11
for(int i=6;i<=10;i++)
{
for(int j=i+1;j<=11;j++)
{
sum+=a[i][j];
count++;
}
}
if(s=='M') printf("%.1lf",sum/count);
else printf("%.1lf",sum);
return 0;
}
*18.平方矩阵 II
输入整数 N,输出一个 N 阶的二维数组。
数组的形式参照样例。
输入格式
输入包含多行,每行包含一个整数 N。
当输入行为 N=0 时,表示输入结束,且该行无需作任何处理。
输出格式
对于每个输入整数 N,输出一个满足要求的 N 阶二维数组。
每个数组占 N行,每行包含 N 个用空格隔开的整数。
每个数组输出完毕后,输出一个空行。
数据范围
0≤N≤100
输入样例:
1
2
3
4
5
0
输出样例:
1
1 2
2 1
1 2 3
2 1 2
3 2 1
1 2 3 4
2 1 2 3
3 2 1 2
4 3 2 1
1 2 3 4 5
2 1 2 3 4
3 2 1 2 3
4 3 2 1 2
5 4 3 2 1参考代码:
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int n;
while(cin>>n,n)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cout<<abs(i-j)+1<<" ";
}
cout<<endl;
}
cout<<endl;
}
return 0;
}*19.平方矩阵 III
输入整数 N,输出一个 N 阶的二维数组 M。
这个 N 阶二维数组满足 M[i][j]=2i+j。
具体形式可参考样例。
输入格式
输入包含多行,每行包含一个整数 N。
当输入行为 N=0 时,表示输入结束,且该行无需作任何处理。
输出格式
对于每个输入整数 N,输出一个满足要求的 N 阶二维数组。
每个数组占 N 行,每行包含 N 个用空格隔开的整数。
每个数组输出完毕后,输出一个空行。
数据范围
0≤N≤15
输入样例:
1
2
3
4
5
0
输出样例:
1
1 2
2 4
1 2 4
2 4 8
4 8 16
1 2 4 8
2 4 8 16
4 8 16 32
8 16 32 64
1 2 4 8 16
2 4 8 16 32
4 8 16 32 64
8 16 32 64 128
16 32 64 128 256
参考代码:
#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
int n;
while (cin >> n, n)
{
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < n; j ++ )
{
int v = 1;
for (int k = 0; k < i + j; k ++ ) v *= 2;
cout << v << ' ';
}
cout << endl;
}
cout << endl;
}
return 0;
}
*20.蛇形矩阵
输入两个整数 n 和 m,输出一个 n 行 m列的矩阵,将数字 1 到 n×m 按照回字蛇形填充至矩阵中。
具体矩阵形式可参考样例。
输入格式
输入共一行,包含两个整数 n和 m。
输出格式
输出满足要求的矩阵。
矩阵占 n 行,每行包含 m 个空格隔开的整数。
数据范围
1≤n,m≤100
输入样例:
3 3
输出样例:
1 2 3
8 9 4
7 6 5参考代码:
#include <iostream>
using namespace std;
int s[100][100];
int main()
{
int n,m;
cin>>n>>m;
int dx[] = {0,1,0,-1},dy[] = {1,0,-1,0};
for(int x=0,y=0,d=0,k=1;k<=m*n;k++)
{
s[x][y]=k;
int a=x+dx[d],b=y+dy[d];
if(a<0 || a>=n || b<0 || b>=m || s[a][b])
{
d=(d+1)%4;
a=x+dx[d],b=y+dy[d];
}
x=a,y=b;
}
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++) cout<<s[i][j]<<" ";
cout<<endl;
}
return 0;
}