论文笔记

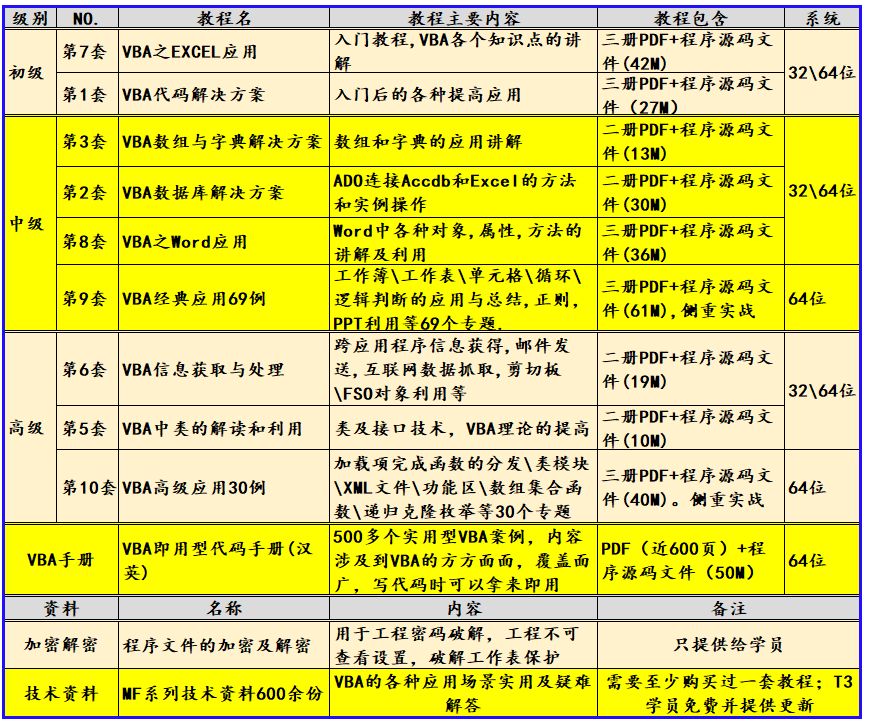
资料

1.代码地址

https://github.com/google-research/sam
https://github.com/davda54/sam

2.论文地址

https://arxiv.org/abs/2010.01412

3.数据集地址

论文摘要的翻译

在当今严重过度参数化的模型中，训练损失的值很难保证模型的泛化能力。事实上，像通常所做的那样，只优化训练损失值很容易导致次优的模型质量。受损失的几何图像与泛化相结合的前人工作的启发，我们引入了一种新的、有效的同时最小化损失值和损失锐度的方法。特别是，我们的方法，锐度感知最小化(SAM)，寻找位于具有一致低损失的邻域的参数；这个公式致使一个最小值-最大值的优化问题，在该问题上可以有效地执行梯度下降。我们提出的经验结果表明，SAM提高了各种基准数据集（例如，CIFAR-{10，100}、ImageNet、微调任务）和模型的模型泛化能力，为几个数据集带来了新的最先进的性能。此外，我们发现SAM原生地提供了对标签噪声的鲁棒性，这与专门针对带有噪声标签的学习的过程所提供的鲁棒性不相上下。

1背景

现代机器学习成功地在广泛的任务中实现了越来越好的性能，这在很大程度上取决于越来越重的过度参数化，以及开发越来越有效的训练算法，这些算法能够找到很好地泛化的参数。事实上，许多现代神经网络可以很容易地记住训练数据，并具有容易过拟合的能力。目前需要这种严重的过度参数化才能在各种领域实现最先进的结果。反过来，至关重要的是，使用程序来训练这些模型，以确保实际选择的参数事实上超越了训练集。
不幸的是，简单地最小化训练集上常用的损失函数（例如，交叉熵）通常不足以实现令人满意的泛化。今天的模型的训练损失景观通常是复杂的和非凸的，具有多个局部和全局极小值，并且具有不同的全局极小值产生具有不同泛化能力的模型。因此，从许多可用的（例如，随机梯度下降、Adam）、RMSProp和其他中选择优化器（和相关的优化器设置）已成为一个重要的设计选择，尽管对其与模型泛化的关系的理解仍处于初级阶段。与此相关的是，已经提出了一系列修改训练过程的方法，包括dropout，批量归一化、随机深度、数据增强和混合样本增强.
损失图像的几何形状——特别是最小值的平坦性和泛化之间的联系已经从理论和实证的角度进行了广泛的研究）。虽然这种联系有望实现新的模型训练方法，从而产生更好的泛化能力，但迄今为止，专门寻找更平坦的最小值并进一步有效提高一系列最先进模型泛化能力的实用高效算法一直难以实现；我们在第5节中对先前的工作进行了更详细的讨论）。

2论文的创新点

• 我们引入了锐度感知最小化(SAM)，这是一种新的方法，通过同时最小化损失值和锐度来提高模型的泛化能力。SAM通过寻找位于具有一致低损耗值的邻域中的参数(而不是仅具有低损耗值的参数，如图1的中间和右侧图像所示)来工作，并且可以高效且容易地实现。

• 我们通过一项严格的实证研究表明，使用SAM提高了一系列广泛研究的计算机视觉任务(例如，CIFAR-{10,100}，ImageNet，微调任务)和模型的模型泛化能力，如图1的左侧曲线图中总结的。例如，应用SAM为许多已经深入研究的任务，如ImageNet，CIFAR-{10,100}，SVHN，Fashion-MNIST，和标准的图像分类微调任务集(例如，Flowers，Stanford Cars，Oxford Pets，等)产生了新的最先进的性能。
• 我们还表明，SAM进一步提供了标签噪声的稳健性，与专门针对带有噪声标签的学习的最先进的程序所提供的一样。
• 通过SAM提供的视角，我们提出了一个很有使用价值的锐度的新概念，我们称之为m-锐度，从而进一步阐明了损失锐度和泛化之间的联系。

3 论文方法的概述

在本文中，我们将标量表示为$a$，将向量表示为$\mathbf{a}$、将矩阵表示为$\mathrm{A}$、将集合表示为$\mathcal{A}$，将等式定义为，。给定训练数据集$\mathcal{S}\triangleq {\cup }_{i=1}^n\{(x_i,y_i)\}$从分布$\mathcal{D},$,中i.i.d.绘制，我们寻求学习一个很好地泛化的模型。特别地，考虑一组由$w\in \mathcal{W}\subseteq {\mathbb{R}}^d$参数化的模型；给定一个逐数据点损失函数$l:\mathcal{W}\times \mathcal{X}\times \mathcal{Y}\to {\mathbb{R}}_{+}$，我们定义了训练集损失$L_S(\mathbf{w})\triangleq \frac{1}{n}{\sum }_{i=1}^{n}l(\mathbf{w},{\mathbf{x}}_i,{\mathbf{y}}_i)$和总体损失$L_{\mathcal{D}}(\mathbf{w})\triangleq {\mathbb{E}}_{(\mathbf{x},\mathbf{y})\sim D}[l(\mathbf{w},\mathbf{x},\mathbf{y})]$。在仅观察到$\mathcal{S}$的情况下，模型训练的目标是选择具有低总体损失$L_{\mathcal{D}}(\mathbf{w})$的模型参数$w$。
利用$L_S(\mathbf{w})作为L_{\mathcal{D}}(\mathbf{w})$的估计，通过使用诸如SGD或Adam之类的优化过程来求解$mi{n}_w{L}_S(\mathbf{w})$（可能与w上的正则化子结合）来激励选择参数w的标准方法。然而，不幸的是，对于现代的过度参数化模型，如深度神经网络，典型的优化方法很容易在测试时导致次优性能。特别地，对于现代模型，$L_S(\mathbf{w})$通常在w中是非凸的，具有多个局部甚至全局最小值，这些局部甚至全局极小值可以产生相似的$L_S(\mathbf{w})$值，同时具有显著不同的泛化性能（即，显著不同的$L_{\mathcal{D}}(\mathbf{w})$值）。
受损失图形的锐度和泛化之间的联系的启发，我们提出了一种不同的方法：我们不是寻找简单地具有低训练损失值$L_S(\mathbf{w})$的参数值$w$，而是寻找整个邻域具有一致低训练损失的参数值（相当于，具有低损失和低曲率的邻域）。以下定理通过在邻域训练损失方面限制泛化能力来说明这种方法的动机（附录A中的完整定理陈述和证明）：

• 定理1
  对于任意$\rho >0$、在由分布$\mathcal{D}$生成的训练集$\mathcal{S}上$具有高概率的情况，$$L_{\mathcal{D}}(\mathbf{w})\le \underset{\Vert \mathbf{ϵ}{\Vert }_2\le \rho }{\max }{L}_{\mathcal{S}}(\mathbf{w}+\mathbf{ϵ})+h(\Vert \mathbf{w}{\Vert }_2^2/{\rho }^2),$$其中h：${\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$是严格递增函数（在$L_{\mathcal{D}}(\mathbf{w})$上的一些技术条件下）。为了明确我们的锐度项，我们可以将上面不等式的右侧重写为为了明确我们的锐度项，我们可以将上面不等式的右侧重写为$[{\max }_{\Vert \mathbf{ϵ}{\Vert }_2\le \rho }{L}_{\mathcal{S}}(\mathbf{w}+\mathbf{ϵ})-L_{\mathcal{S}}(\mathbf{w})]+L_{\mathcal{S}}(\mathbf{w})+h(\Vert \mathbf{w}{\Vert }_2^2/{\rho }^2).$
  方括号中的项通过测量通过从$w$移动到附近的参数值可以以多快的速度增加训练损失来捕捉$L_S$在$w$处的锐度；然后将该锐度项与训练损失值本身和$w$大小上的正则化子求和。给定特定函数h深受证明细节的影响，我们用$\lambda ||w|{|}_2^2$代替超参数λ的第二项，得到标准L2正则化项。因此，受约束项的启发，我们建议通过解决以下SharpnessAware最小化（SAM）问题来选择参数值：
  $$\underset{\mathbf{w}}{\min }{L}_{\mathcal{S}}^{SAM}(\mathbf{w})+\lambda \Vert \mathbf{w}{\Vert }_2^2\mathrm{where}{L}_{\mathcal{S}}^{SAM}(\mathbf{w})\triangleq \underset{||\mathbf{ϵ}|{|}_p\le \rho }{\max }{L}_S(\mathbf{w}+\mathbf{ϵ}),$$其中$\rho \ge 0$是一个超参数，$p\in [1，\infty ]$（我们在最大化过程中从L2范数略微推广到p范数，本文已经证明$p=2$通常是最优的）。图1显示了1通过最小化$L_S(\mathbf{w})$或$L_S^{SAM}(\mathbf{w})$而收敛到最小值的模型的损失情况，说明了锐度感知损失阻止了模型收敛到尖锐的最小值。
  为了最小化$L_S^{SAM}(\mathbf{w})$，我们通过内部最大化进行微分，推导出了一个有效的近似值，从而使我们能够将随机梯度下降直接应用于SAM目标。沿着这条路前进，我们首先通过$L_{\mathcal{S}}(w+ϵ)w.r.t.ϵ$ 在0附近的一阶泰勒展开来近似内部最大化问题，得到$$\begin{gathered} \mathbf{ϵ} \\ \mathbf{w})\triangleq \arg \underset{\Vert \mathbf{ϵ}{\Vert }_p\le \rho }{\max }{L}_{\mathcal{S}}(\mathbf{w}+\mathbf{ϵ})\approx \arg \underset{\Vert \mathbf{ϵ}{\Vert }_p\le \rho }{\max }{L}_{\mathcal{S}}(\mathbf{w})+{\mathbf{ϵ}}^T{\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(\mathbf{w})=\arg \underset{\Vert \mathbf{ϵ}{\Vert }_p\le \rho }{\max }{\mathbf{ϵ}}^T{\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(\mathbf{w}). \end{gathered}$$反过来，求解该近似的值$\xi (w)$由经典对偶范数问题的解给出（$|\cdot {|}^{q-1}$表示元素绝对值和幂）：$$\widehat{\mathbf{ϵ}}(w)=\rho \mathrm{sign}\left({\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(w)\right)|{\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(w){|}^{q-1}/{\left(\Vert {\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(w){\Vert }_q^q\right)}^{1/p}\text{(2)}$$其中1/p+1/q＝1。代入方程（1）并进行微分，我们得到$${\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}^{SAM}(\mathbf{w})\approx {\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(\mathbf{w}+\widehat{\mathbf{ϵ}}(\mathbf{w}))=\frac{d(\mathbf{w}+\widehat{\mathbf{ϵ}}(\mathbf{w}))}{d\mathbf{w}}{\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(\mathbf{w}){|}_{\mathbf{w}+\widehat{\mathbf{ϵ}}(w)}$$
  可以通过自动微分直接计算这种对${\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}^{SAM}(w)$的近似，如在JAX、TensorFlow和PyTorch等公共库中实现的那样。尽管该计算隐含地依赖于LS（w）的Hessian，因为ξ。获得我们的最终梯度近似：$${\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}^{SAM}(\mathbf{w})\approx {\nabla }_{\mathbf{w}}{L}_{\mathcal{S}}(w){|}_{\mathbf{w}+\widehat{\mathbf{ϵ}}(\mathbf{w})}.$$
  我们通过将标准数值优化器（如随机梯度下降（SGD））应用于SAM目标$L_{\mathcal{S}}^{SAM}(\mathbf{w})$，使用方程3来计算必要的目标函数梯度，从而获得最终的SAM算法。算法1给出了完整SAM算法的伪代码，使用SGD作为基本优化器，图2示意性地说明了单个SAM参数更新。
  

4 论文实验

为了评估SAM的功效，我们将其应用于一系列不同的任务，包括从头开始的图像分类（包括在CIFAR-10、CIFAR-100和ImageNet上）、微调预训练的模型以及使用噪声标签进行学习。在所有情况下，我们都通过简单地用SAM代替用于训练现有模型的优化程序来衡量使用SAM的好处，并计算由此对模型泛化的影响。如下所示，SAM在绝大多数情况下都能显著提高泛化性能。

4.1 图像分类

我们首先评估了SAM对当今最先进的CIFAR-10和CIFAR-100模型（无需预训练）泛化的影响：具有ShakeShake正则化的WideResNets和具有ShakeDrop正则化的PyramidNet。请注意，这些模型中的一些已经在先前的工作中进行了大量调整，并包括精心选择的正则化方案，以防止过拟合；因此，显著提高它们的泛化能力是非常重要的。我们已经确保在没有SAM的情况下，我们的实现的泛化性能与先前工作中报告的性能相匹配或超过。
所有结果都使用了基本数据增强（水平翻转、四像素填充和随机裁剪）。我们还评估了更先进的数据增强方法，如剪切正则化和AutoAugment（，这些方法被先前的工作用来实现最先进的结果。
SAM具有单个超参数$\rho （邻域大小）$，我们使用10%的训练集作为验证集，通过在 { 0.01 ， 0.02 ， 0.05 ， 0.1 ， 0.2 ， 0.5 } \{0.01，0.02，0.05，0.1，0.2，0.5\} {0.01，0.02，0.05，0.1，0.2，0.5}上的网格搜索对其进行调整。有关所有超参数的值和其他训练细节，请参见附录C.1。由于每个SAM权重更新需要两个反向传播操作（一个用于计算$\xi （w）$，另一个用于估计最终梯度），我们允许每个非SAM训练运行执行两倍于每个SAM训练运行的轮次，并且我们报告每个非SAM训练运行在标准轮次计数或加倍轮次计数上获得的最佳得分。我们运行每个实验条件的五个独立副本，报告结果（每个条件都有独立的权重初始化和数据混洗），报告测试集的平均误差（或准确性）以及相关的95%置信区间。我们的实现使用JAX，并且我们在具有8个NVidia V100 GPU的单个主机上训练所有模型。为了在跨多个加速器并行时计算SAM更新，我们在加速器之间均匀地划分每个数据批次，独立地计算每个加速器上的SAM梯度，并对得到的子批次SAM梯度进行平均，以获得最终的SAM更新。
如表1所示，SAM提高了针对CIFAR-10和CIFAR-100评估的所有设置的泛化能力。例如，SAM使简单的WideResNet能够获得1.6%的测试误差，而没有SAM时的误差为2.2%。这种增益以前只能通过使用更复杂的模型架构（例如，PyramidNet）和正则化方案（例如，Shake-Shake、ShakeDrop）来实现；SAM提供了一个易于实施的、独立于模型的替代方案。此外，即使在已经使用复杂正则化的复杂架构上应用SAM，SAM也能提供改进：例如，将SAM应用于具有ShakeDrop正则化的PyramidNet，在CIFAR-100上产生10.3%的误差，据我们所知，这是该数据集上的一个新的最先进技术，无需使用额外数据。

除了CIFAR-{101100}之外，我们还在SVHN和Fashion MNIST数据集上评估了SAM。再次，SAM使一个简单的WideResNet能够实现这些数据集达到或高于最先进水平的精度：SVHN的误差为0.99%，Fashion MNIST为3.59%。详细信息见附录B.1。
为了更大规模地评估SAM的性能，我们将其应用于在ImageNet上训练的不同深度（50，101，152）的ResNets。在这种情况下，根据先前的工作，我们将图像调整大小并裁剪到224像素分辨率，对其进行归一化，并使用批量大小4096、初始学习率1.0、余弦学习率计划、动量为0.9的SGD优化器、标签平滑度为0.1和权重衰减0.0001。当应用SAM时，我们使用ρ=0.05（通过对训练了100个时期的ResNet-50进行网格搜索确定）。我们使用Google Cloud TPU3在ImageNet上训练所有模型长达400个时期，并报告每个实验条件的前1和前5测试错误率（5次独立运行的平均值和95%置信区间）。
如表2所示，SAM再次持续提高性能，例如将ResNet-152的ImageNet top 1错误率从20.3%提高到18.4%。此外，请注意，SAM能够增加训练时期的数量，同时在不过度拟合的情况下继续提高准确性。相反，当训练从200个时期扩展到400个时期时，标准训练过程（没有SAM）通常显著地过拟合。

4.2 微调

通过在大型相关数据集上预训练模型，然后在感兴趣的较小目标数据集上进行微调，迁移学习已成为一种强大且广泛使用的技术，用于为各种不同的任务生成高质量的模型。我们在这里展示了SAM在这种情况下再次提供了相当大的好处，即使在微调非常大、最先进、已经高性能的模型时也是如此。
特别地，我们将SAM应用于微调EfficientNet-b7（在ImageNet上预训练）和EfficientNet-L2（在ImageNet上预训练加上未标记的JFT；输入分辨率475）。我们将这些模型初始化为公开可用的检查点6，分别用RandAugment（在ImageNet上的准确率为84.7%）和NoisyStudent（在Image Net上的正确率为88.2%）训练。我们通过从上述检查点开始训练每个模型，在几个目标数据集中的每个数据集上微调这些模型；有关使用的超参数的详细信息，请参阅附录。我们报告了每个数据集在5次独立运行中前1个测试误差的平均值和95%置信区间。
如表3所示，相对于没有SAM的微调，SAM均匀地提高了性能。此外，在许多情况下，SAM产生了新的最先进的性能，包括CIFAR-10上0.30%的误差、CIFAR-100上3.92%的误差和ImageNet上11.39%的误差。

4.3对标签噪声的鲁棒性

SAM寻找对扰动具有鲁棒性的模型参数这一事实表明，SAM有可能在训练集中提供对噪声的鲁棒性（这将扰乱训练损失景观）。因此，我们在这里评估SAM为标记噪声提供的鲁棒性程度。
特别地，我们测量了在CIFAR-10的经典噪声标签设置中应用SAM的效果，其中训练集的一小部分标签被随机翻转；测试集保持未修改（即干净）。为了确保与之前的工作进行有效的比较，之前的工作通常使用专门用于噪声标签设置的架构，我们在Jiang等人之后，为200个时期训练了一个类似大小的简单模型（ResNet-32）。我们评估了模型训练的五种变体：标准SGD、带Mixup的SGD、SAM和带MixupSAM的“自举”SGD变体（其中，首先像往常一样训练模型，然后在最初训练的模型预测的标签上从头开始重新训练）。当应用SAM时，我们对除80%之外的所有噪声级使用ρ=0.1，对于80%，我们使用ρ=0.05来获得更稳定的收敛。对于混合基线，我们尝试了α∈{1，8，16，32}的所有值，并保守地报告每个噪声水平的最佳得分。
如表4所示，SAM提供了对标签噪声的高度鲁棒性，与专门针对具有噪声标签的学习的现有技术程序所提供的鲁棒性不相上下。事实上，除了MentorMix（之外，简单地用SAM训练模型胜过所有专门针对标签噪声鲁棒性的现有方法。然而，简单地自举SAM产生的性能与MentorMix相当（后者要复杂得多）。

5 SAM视角下的锐度与泛化

5.1 m-锐度

尽管我们对SAM的推导定义了整个训练集的SAM目标，但当在实践中使用SAM时，我们计算每个批次的SAM更新（如算法1所述），甚至通过平均每个加速器独立计算的SAM更新来计算（其中每个加速器接收一个批次的大小为m的子集，如第3节所述）。后一种设置等效于修改SAM目标（等式1）以在一组独立的最大化上求和，每个最大化对m个数据点的不相交子集上的每个数据点损失的总和执行，而不是在训练集上的全局总和上执行最大化（这将等效于将m设置为总训练集大小）。我们将损失图像的锐度的相关度量称为m-锐度。

为了更好地理解m对SAM的影响，我们在CIFAR-10上使用m值范围的SAM训练一个小的ResNet。如图3（中间）所示，较小的m值往往产生具有更好泛化能力的模型。这种关系恰好符合跨多个加速器并行化的需要，以便为当今的许多模型扩展训练。有趣的是，如图3（右）所示，随着m的减少，上述m锐度测量进一步与模型的实际泛化差距表现出更好的相关性。特别地，这意味着，与上述定理1所建议的全训练集测度相比，m<n的m-清晰度产生了更好的泛化预测因子，这为理解泛化提供了一条有趣的新途径。

5.2 HESSIAN SPECTRA

受损失图像的几何形状和泛化之间的联系的启发，我们构建了SAM，以寻找具有低损失值和低曲率（即，低锐度）的训练损失图像的最小值。为了进一步证实SAM确实发现了具有低曲率的极小值，我们计算了在CIFAR-10上训练300步的WideResNet40-10在训练期间的不同时期的Hessian谱，包括有SAM和没有SAM（没有批处理规范，这往往会模糊对Hessian的解释）。由于参数空间的维数，我们使用Lanczos算法来近似Hessian谱。
图3（左）报告了由此产生的Hessian光谱。正如预期的那样，用SAM训练的模型收敛到具有较低曲率的最小值，如在特征值的总体分布中所见，收敛时的最大特征值（${\lambda }_{max}$）（无SAM时约为24，有SAM时为1.0），以及大部分频谱（比率${\lambda }_{max}/{\lambda }_5$，通常用作锐度的代理；在没有SAM的情况下高达11.4，在有SAM的情况中高达2.6）。

6 总结

在这项工作中，我们引入了SAM，这是一种新的算法，通过同时最小化损失值和损失清晰度来提高泛化能力；我们已经通过严格的大规模实证评估证明了SAM的有效性。我们已经为未来的工作提供了许多有趣的途径。在理论方面，m-锐度产生的每个数据点-锐度的概念（与过去通常研究的在整个训练集上计算的全局清晰度形成对比）提出了一个有趣的新视角，通过它来研究泛化。从方法上讲，我们的结果表明，在目前依赖Mixup的稳健或半监督方法中，SAM有可能取代Mixup（例如，提供MentorSAM）。