滑动窗口算法介绍
所谓滑动窗口,即为同向双指针移动过程中形成的间隔区域,并且这两个指针在移动的过程中不会回退
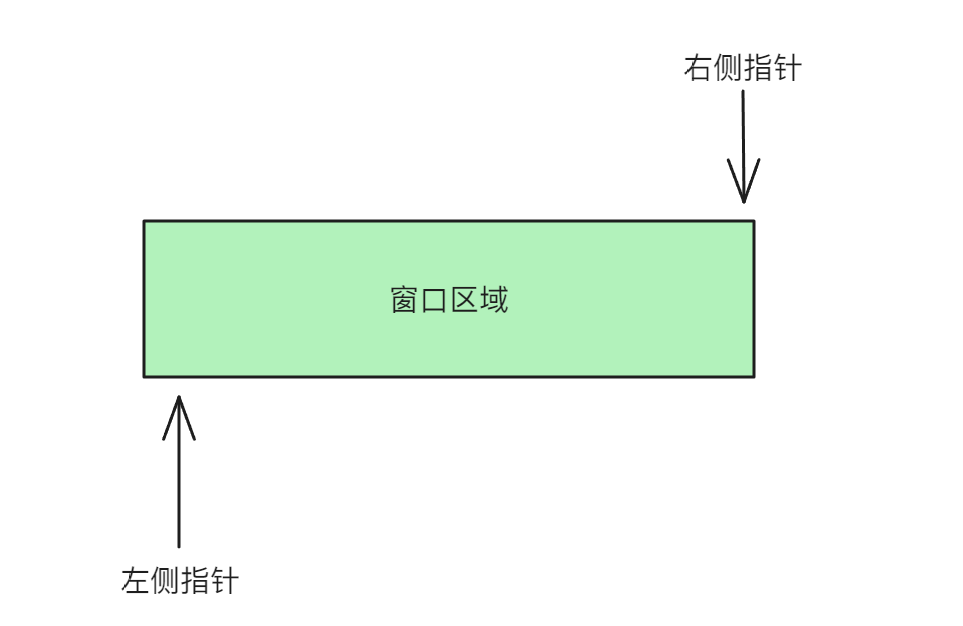
对于滑动窗口的题目可以抽象为三个步骤:
- 定义窗口两端指针
left和right - 进入窗口
- 判断
- 离开窗口
- 循环2、3和4步
滑动窗口练习
长度最小的子数组
题目链接:209. 长度最小的子数组 - 力扣(LeetCode)
给定一个含有n个正整数的数组和一个正整数target。
找出该数组中满足其总和大于等于target的长度最小的 子数组[numsl, numsl+1, ..., numsr-1, numsr],并返回其长度**。**如果不存在符合条件的子数组,返回0。
思路解析:
以下面的数组为例
[ 2,3,1,2,4,3 ]本题首先想到的就是暴力解法,暴力解法的思路很简单,第一层for循环遍历,选出区间左端点,第二层for循环遍历,选出区间右端点,最后一次遍历,将左右区间中的值全部相加求和,标记此时子数组的长度,如此往复直到找到子数组长度最小且子数组中元素之和>=target。根据这个暴力思路得出其时间复杂度为O()
// 暴力解法
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int len = INT_MAX;
for(int i = 0; i < nums.size(); i++)
{
for(int j = 0; j < nums.size(); j++)
{
int sum = 0;
for(int k = i; k <= j; k++)
{
sum += nums[k];
if(sum >= target)
{
len = min(len, j - i + 1);
}
}
}
}
return len == INT_MAX ? 0 : len;
}
};在暴力思路的基础上思考如何降低时间复杂度
单调性:因为题目给出了一个条件正整数的数组,在正整数范围内求和可以得到一个单调性的规律:加的数字越多和越大,所以如果第一次找到了一个和满足>=target,则该下标后的数值即可不需要遍历,例如下图中的4和3即可不需要遍历

正向性:因为在上一次的遍历过程中,已经找到了一组子数组和满足>=target,并且根据单调性可以得出right不需要再向后移动,接下来需要更新left寻找下一组此时left++,那么此时right是否需要回退到left的位置重新再来一次遍历呢?答案是不需要,因为left++,此时区间[left, right]是开始时(left=0)[left, right]区间的子区间,所以此时的区间(left=1)[left, right]中的元素和即为开始元素和-left=0时的值,所以可以得出,right在整个遍历过程中是不需要回退的,即保持正向移动,而left本身移动的方向为从左向右,所以left方向也是正向的
由以上两个性质,可以将暴力解法优化到O(N),即只需要一次遍历,而结合上面两种优化方式,可以得出滑动窗口算法
在本题中,滑动窗口的两端即为left和right,而滑动窗口中所维护的信息即为子数组之和sum,根据滑动窗口的基本解题步骤可以得出现在需要找到何时进窗口、判断以及何时出窗口
- 何时进窗口:本题中,因为窗口中维护的信息是
sum,所以当开始求和时即为进窗口 - 判断:本题中,因为需要判断
sum>=target,所以此为判断条件 - 何时出窗口:本题中,根据判断条件
sum>=target可以得出,此条件成立时,证明已经得出了一个合理的结果,需要更新sum和子数组长度len,并让left向后移动(移动窗口,即出窗口),这一过程被称为更新结果(更新结果一般是贯穿在滑动窗口的解题步骤中,具体在哪一步由题目决定)
需要注意,本题需要求出子数组长度的最小值,所以
len不可以初始化为0,否则最后结果只会为0
具体步骤如下:
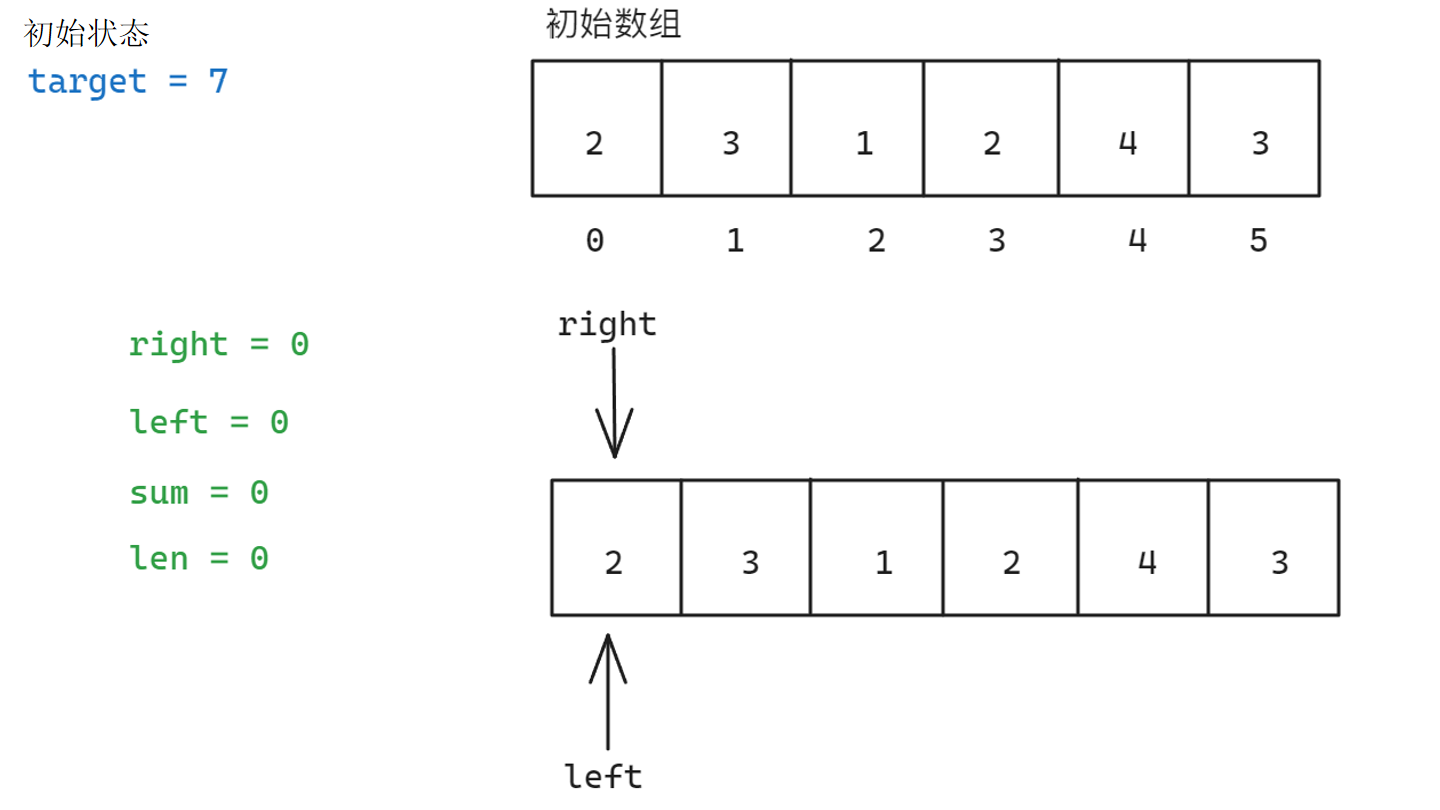
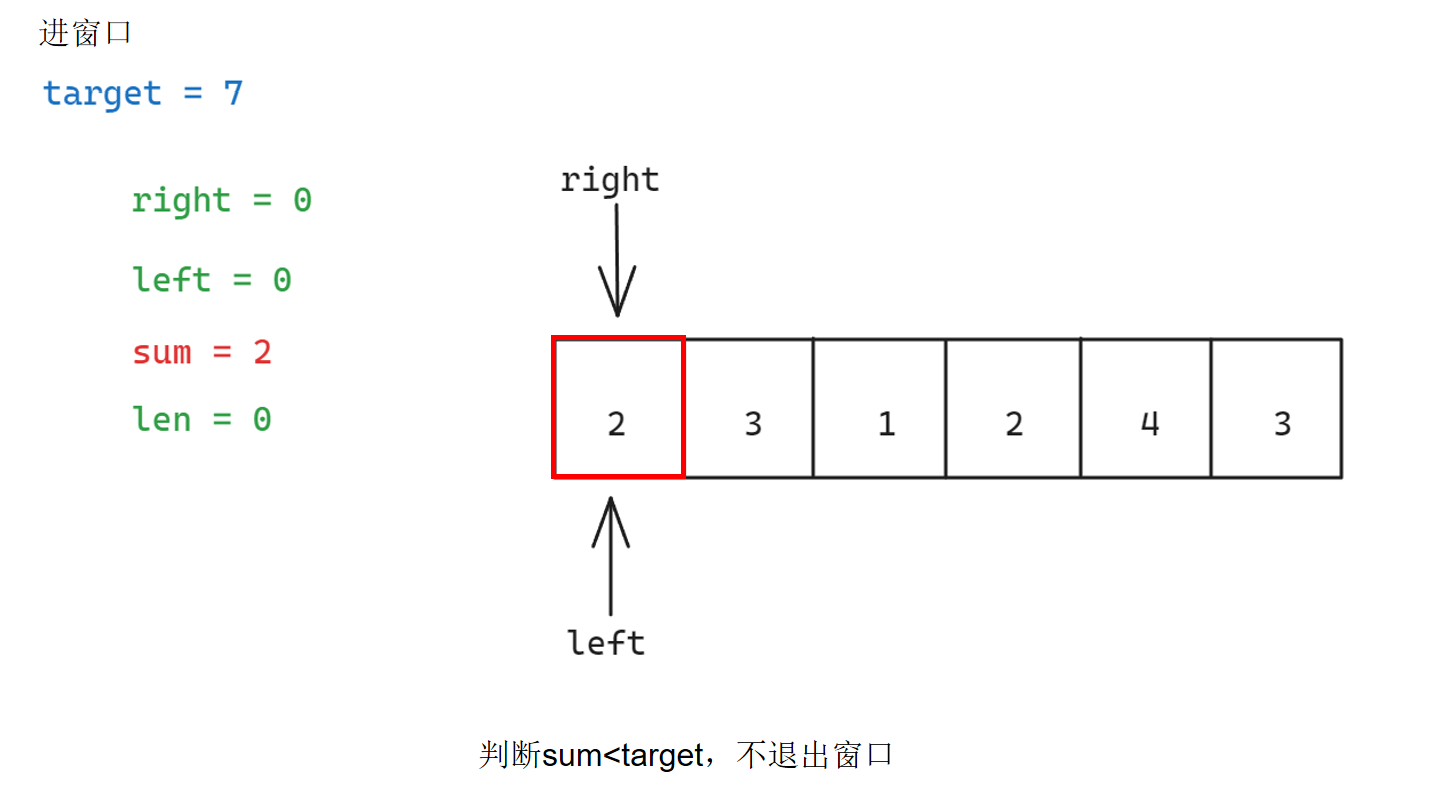

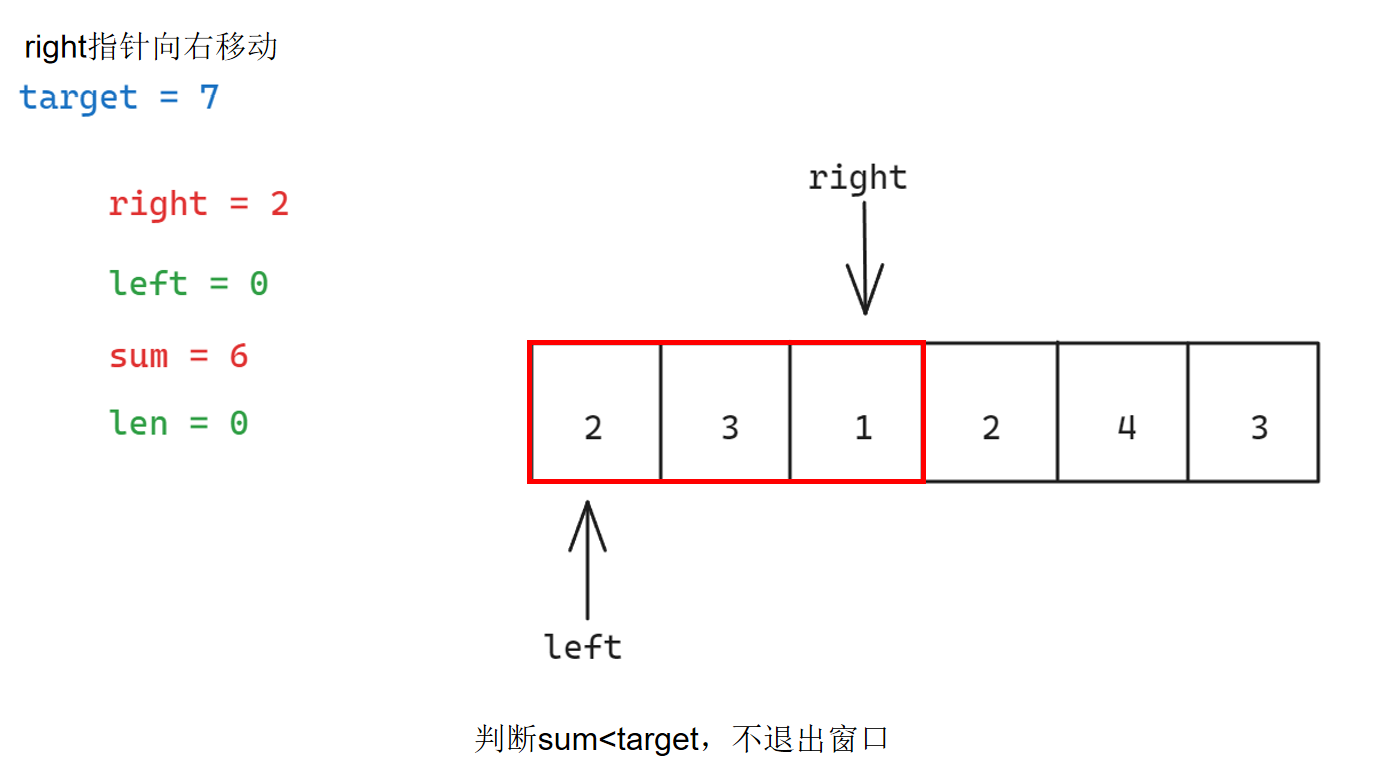
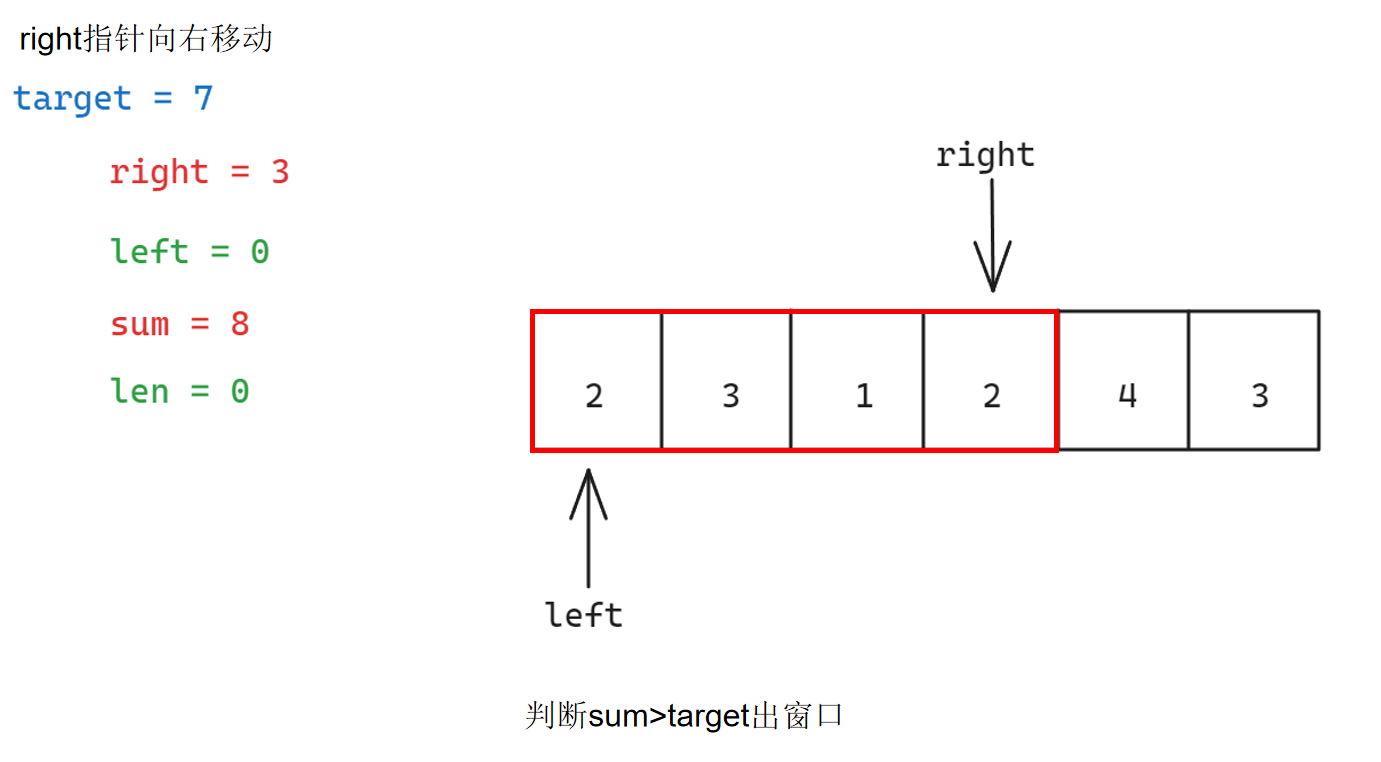
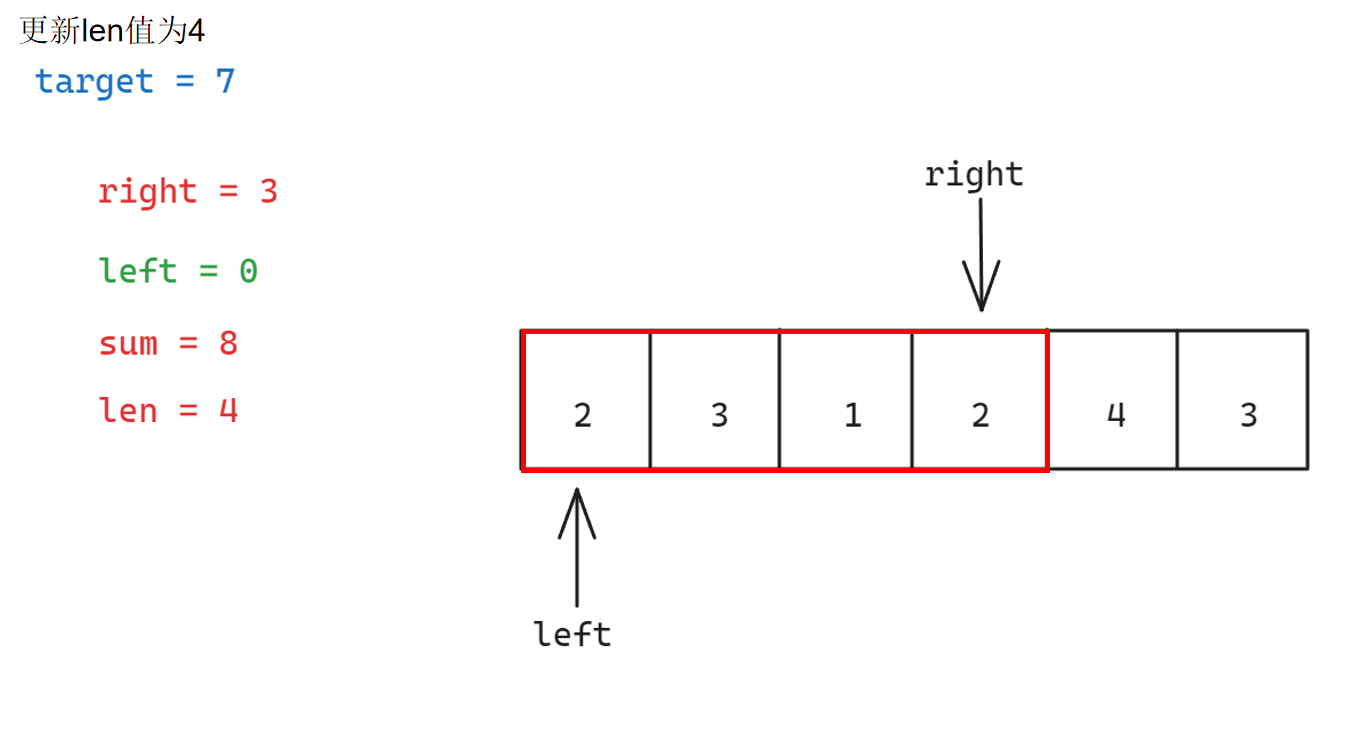
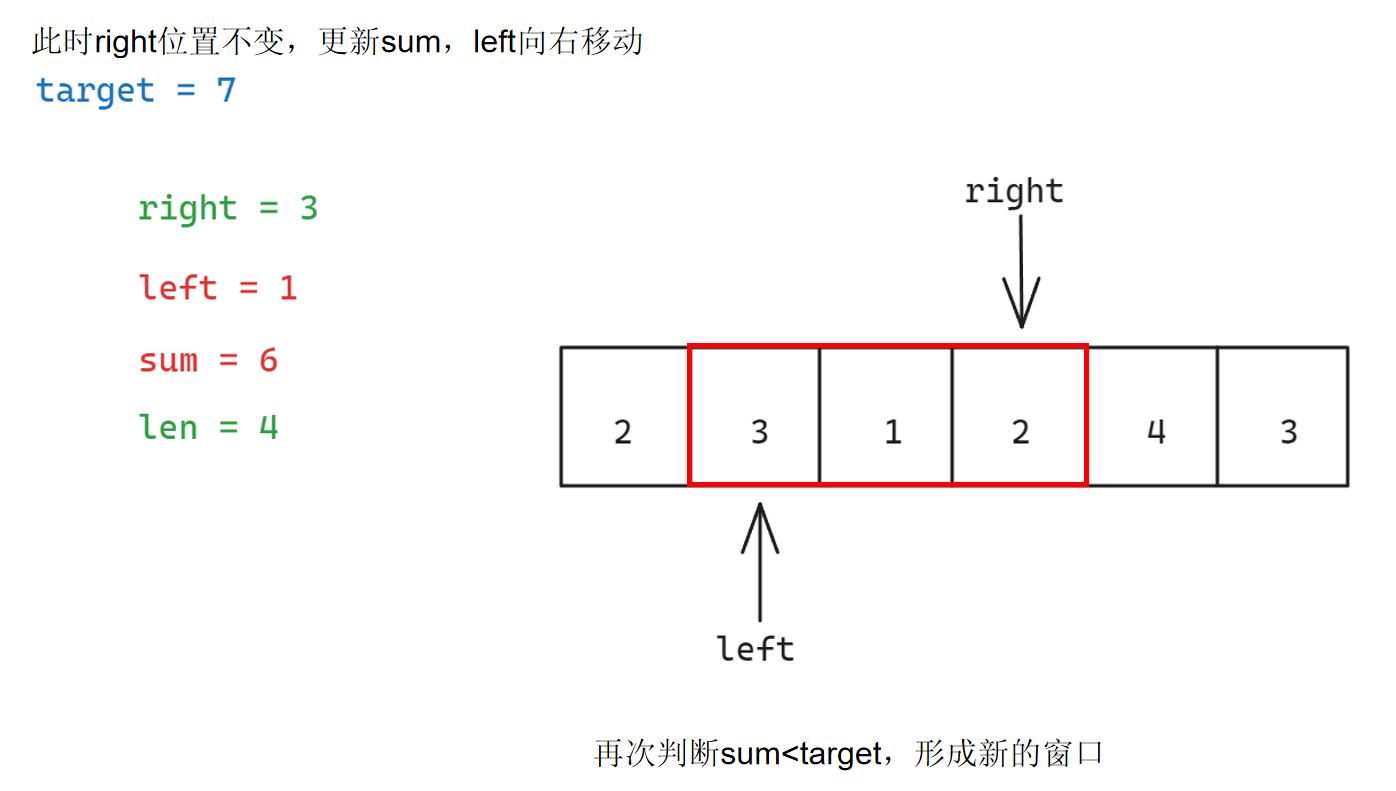
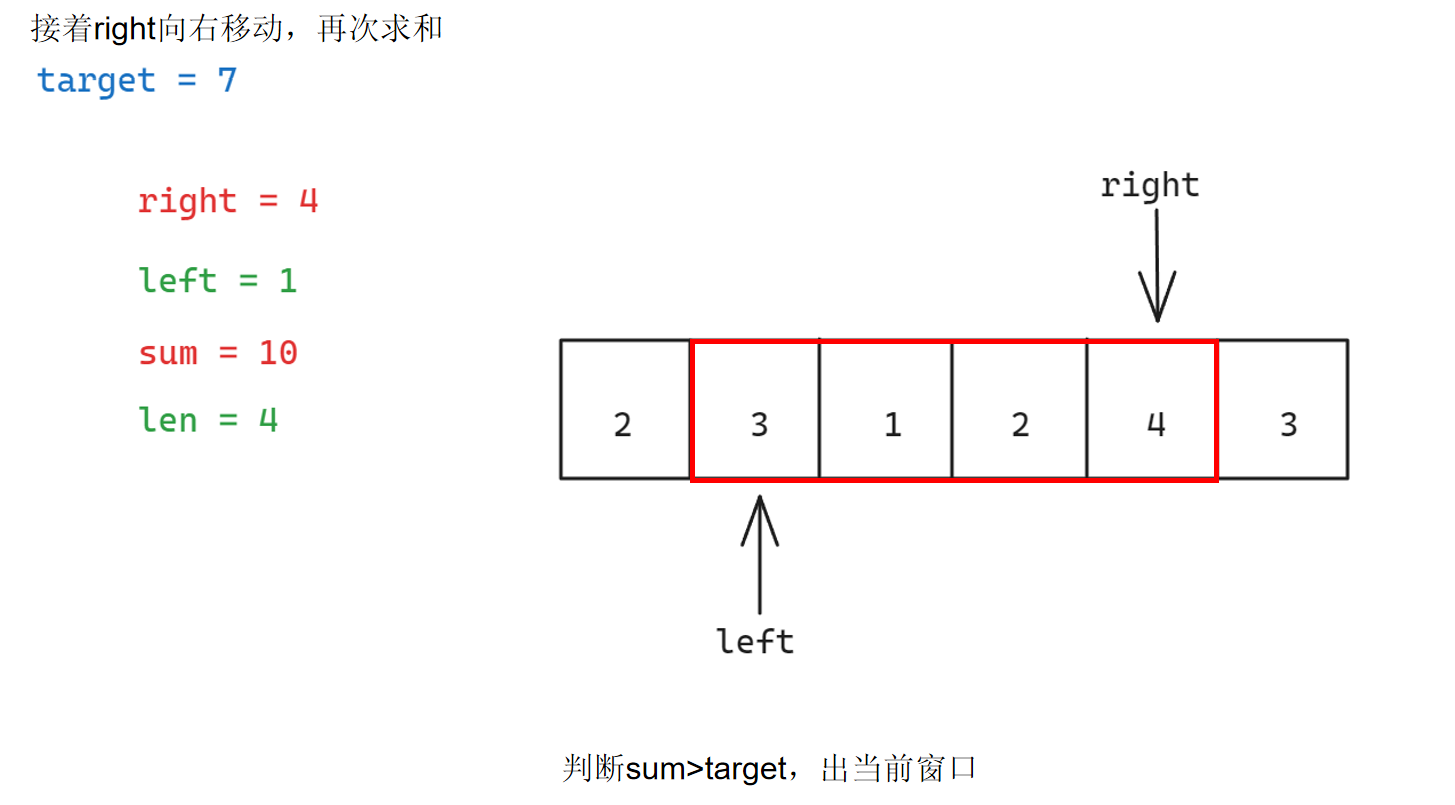
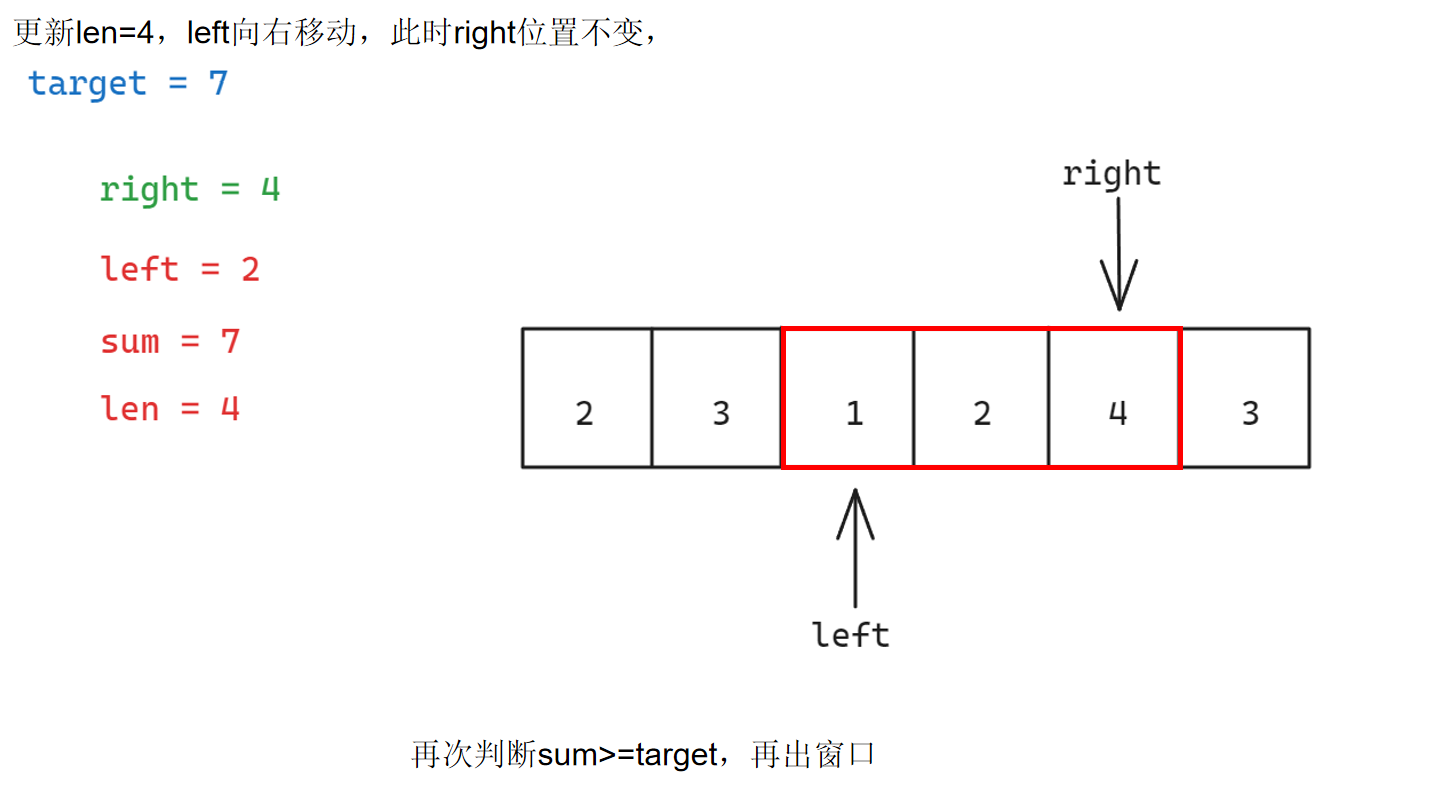
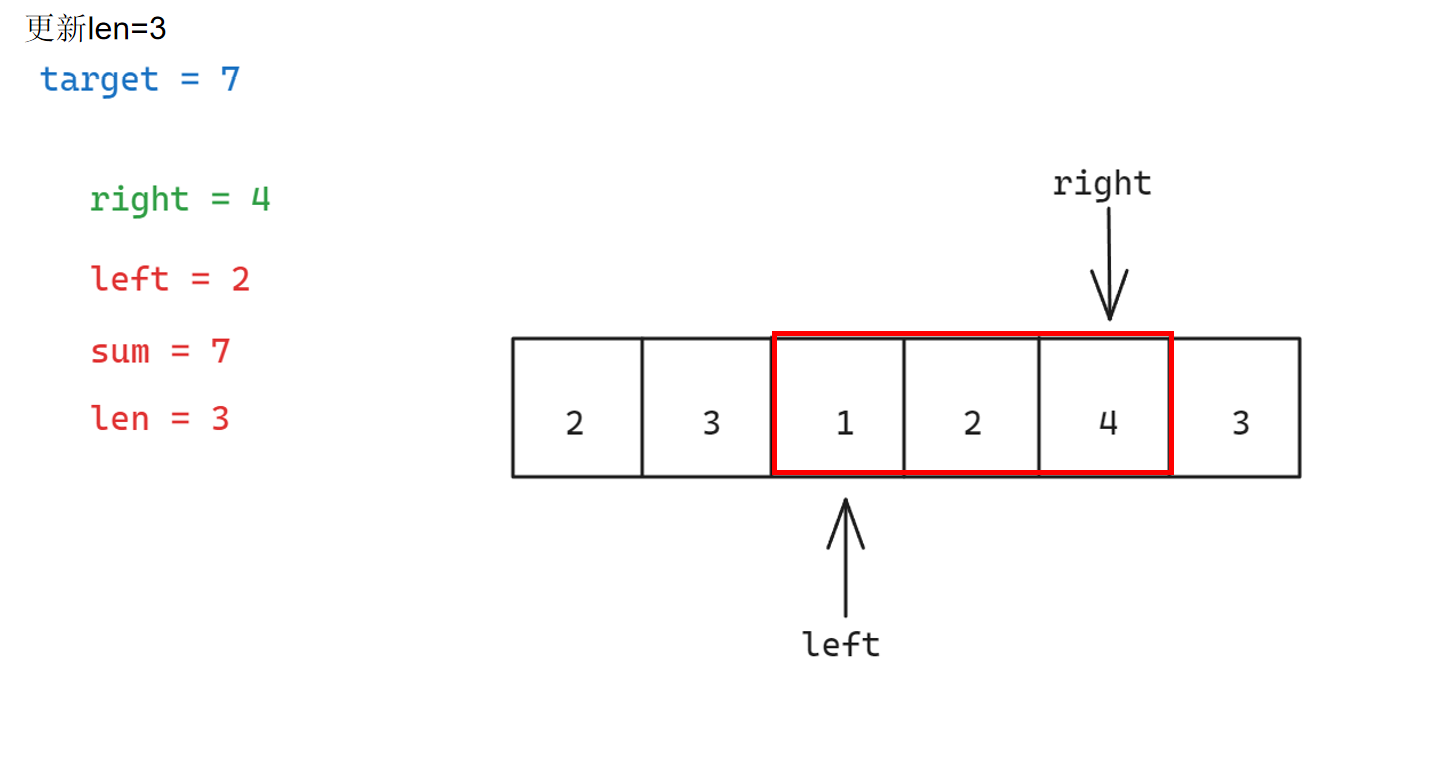
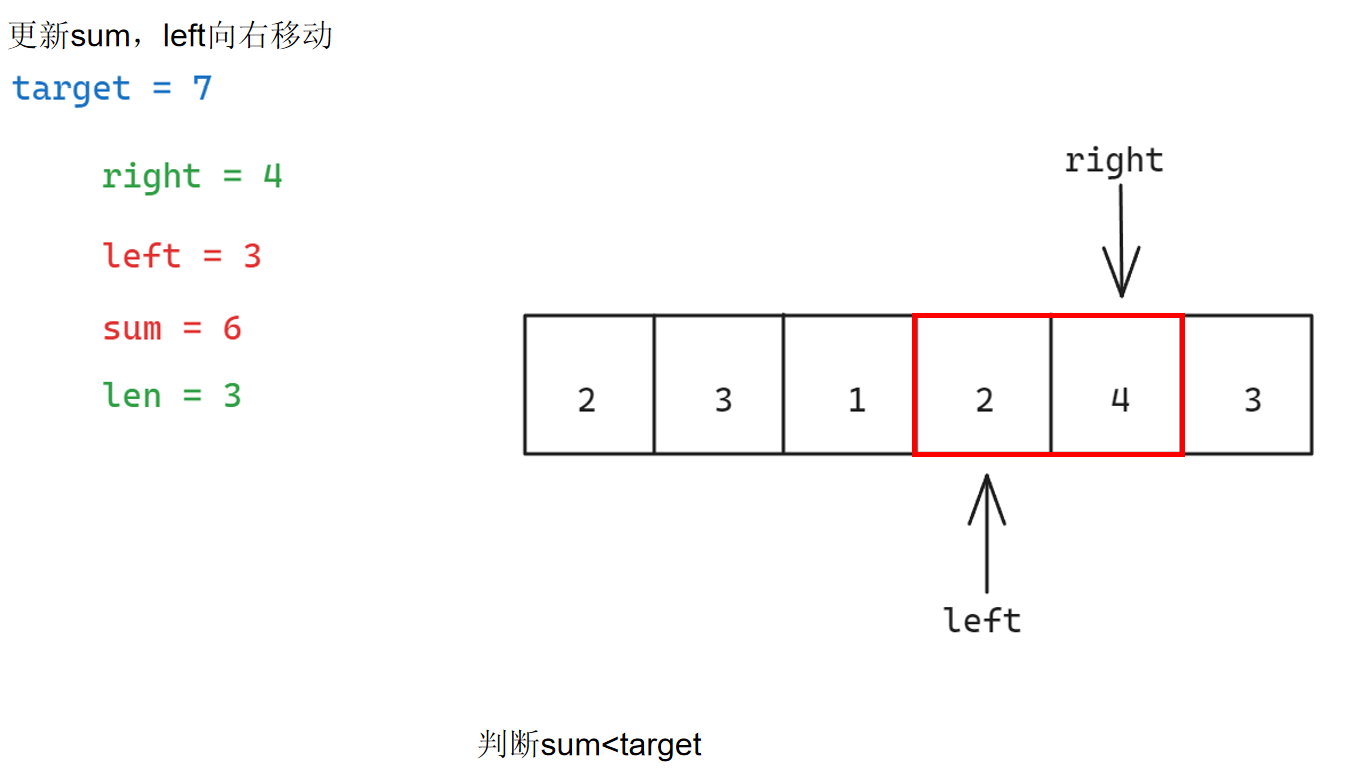
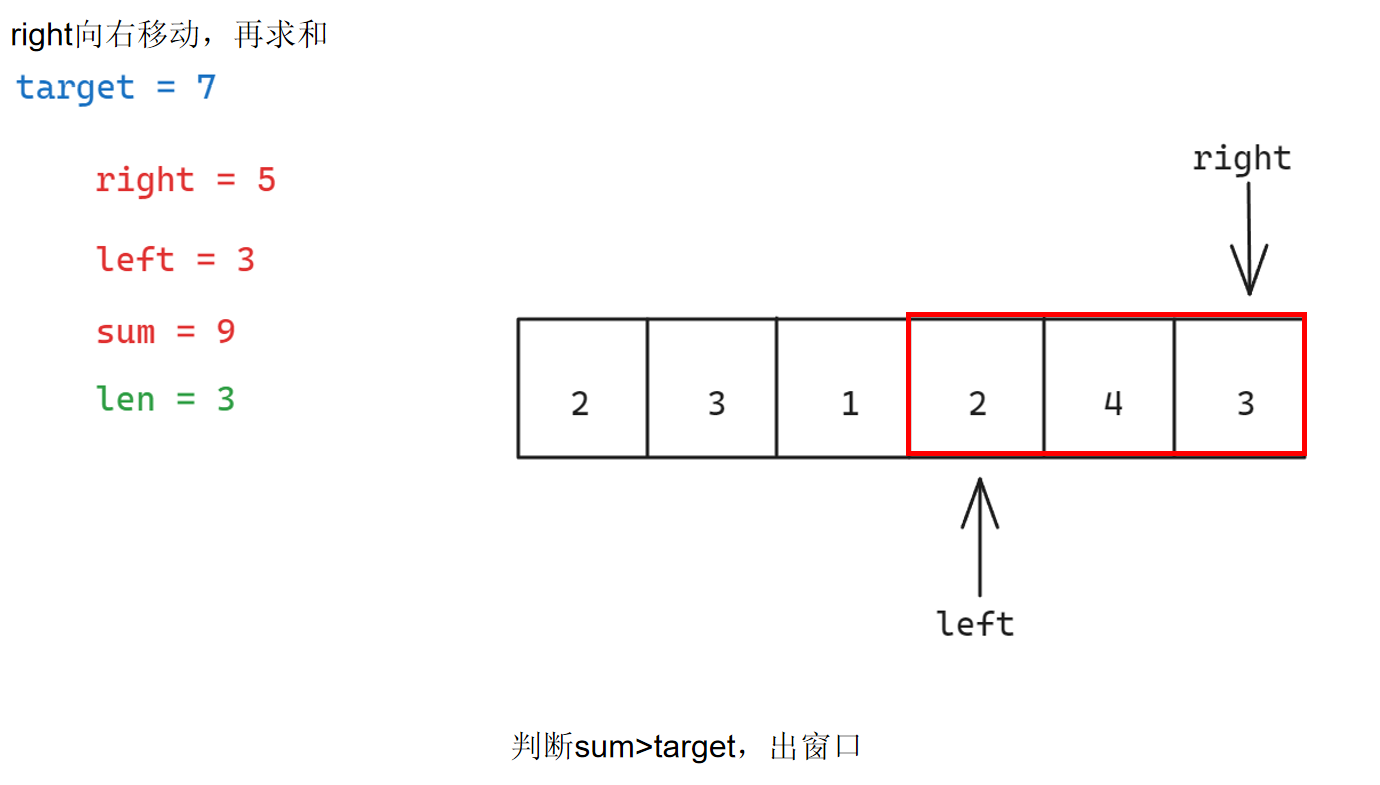
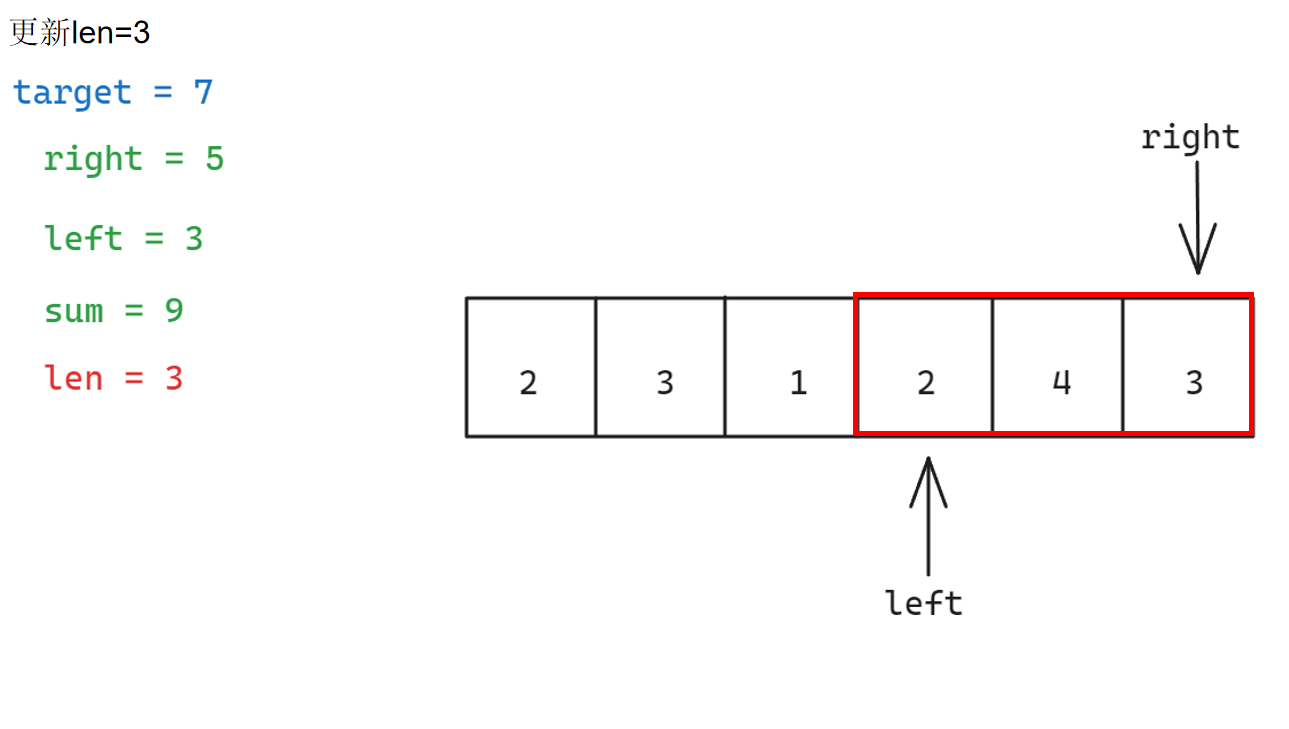
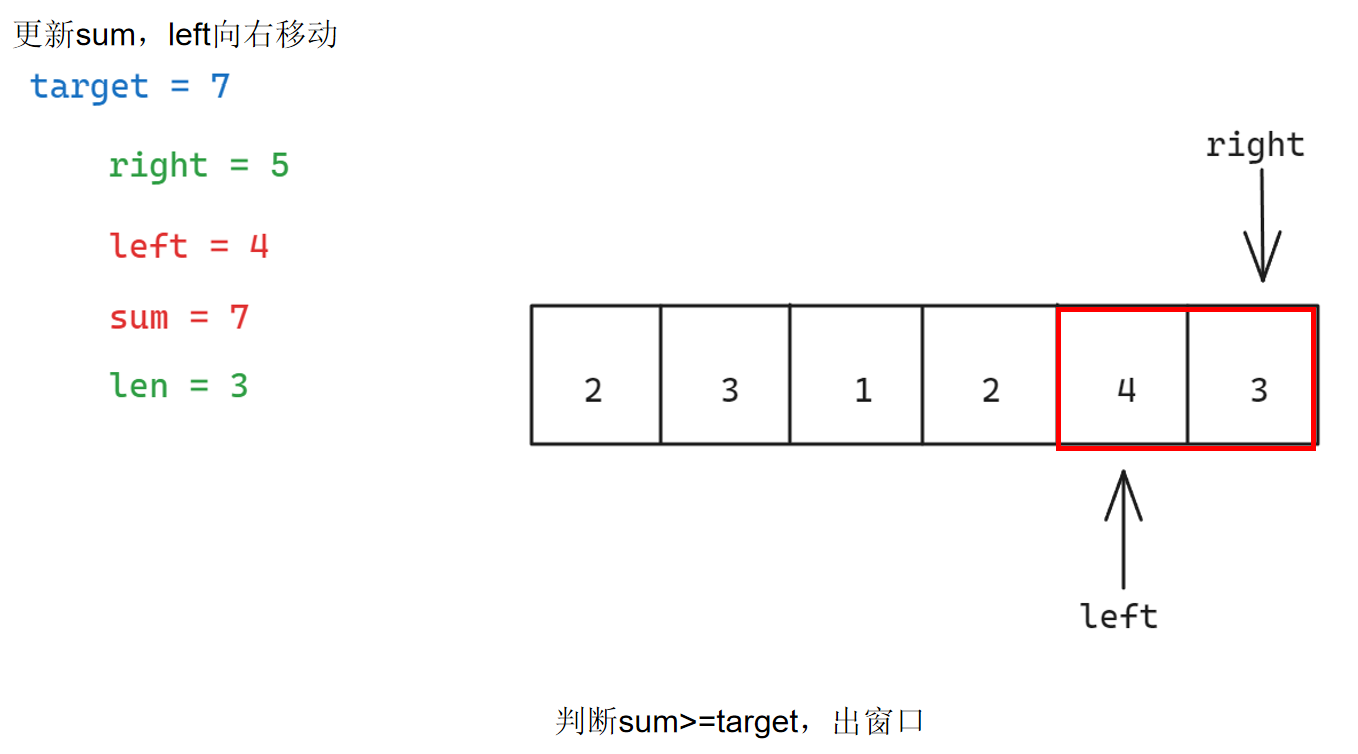
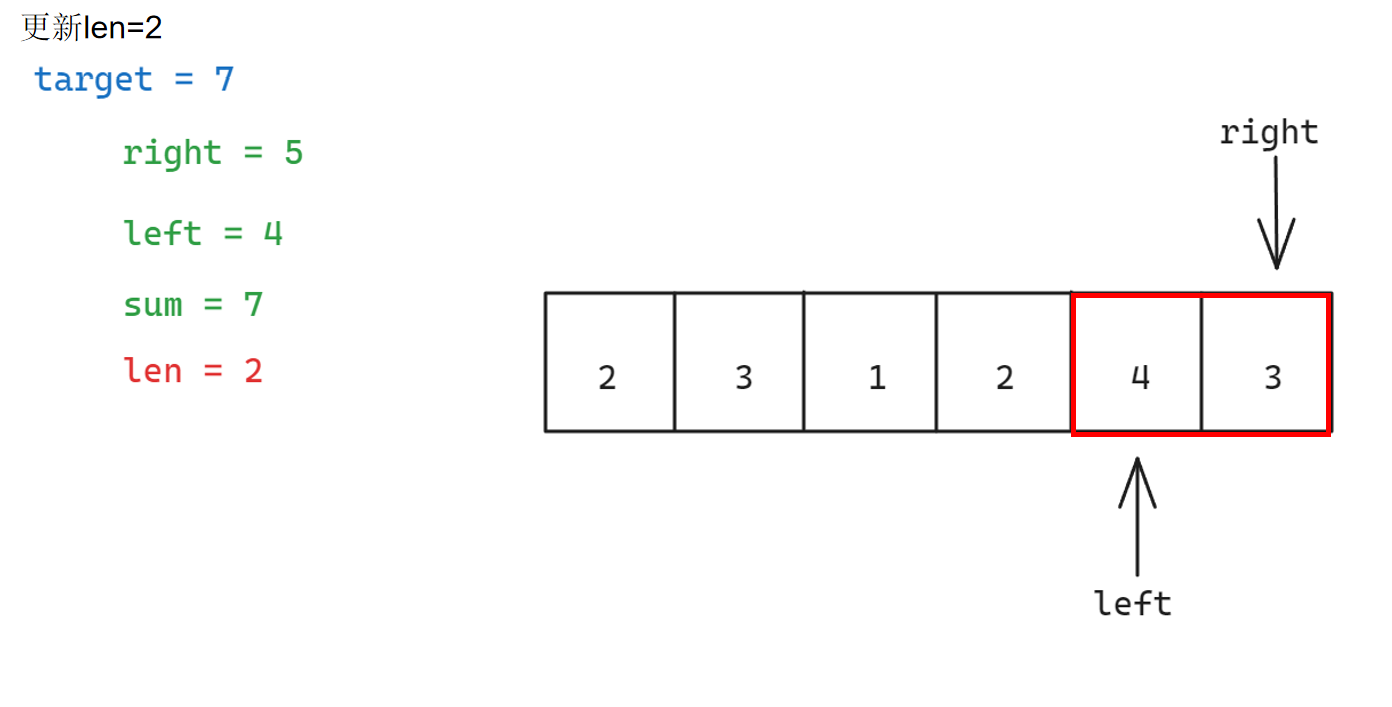
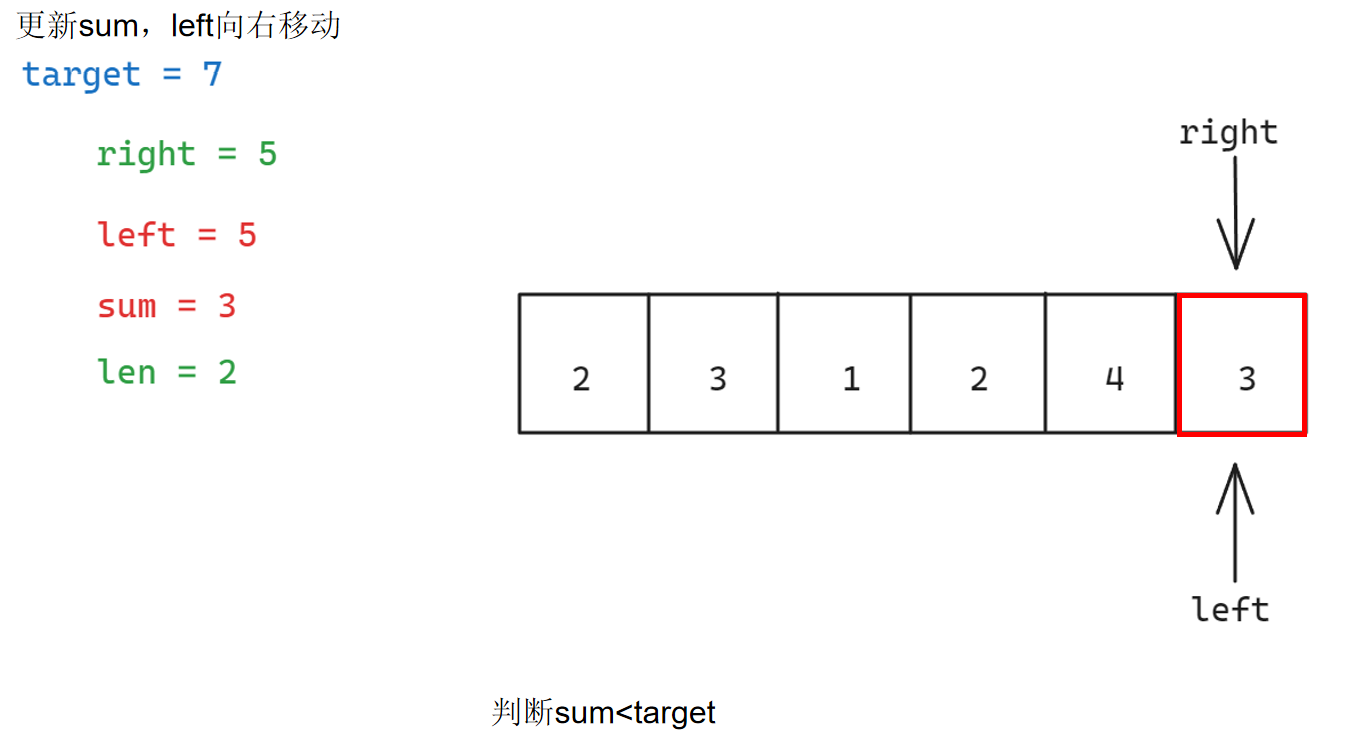
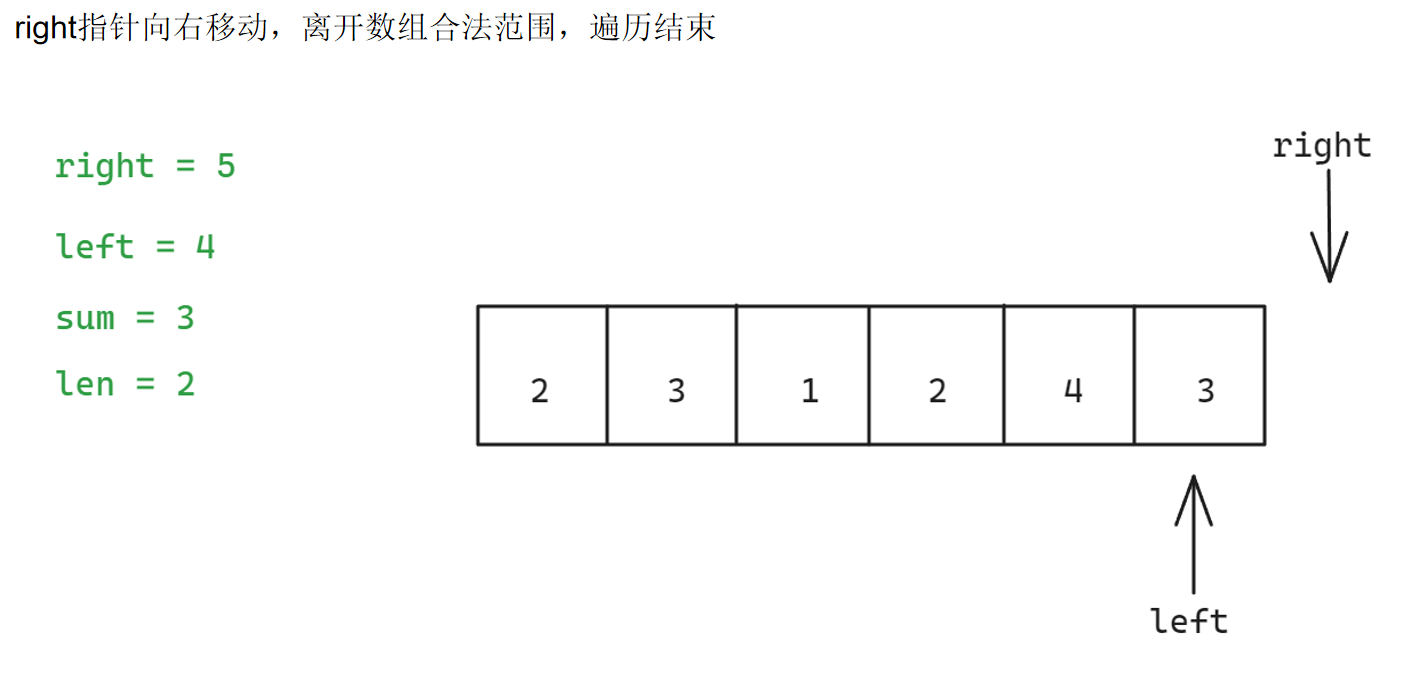
参考代码如下:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int len = INT_MAX, size = nums.size();
int sum = 0;
for(int left = 0, right = 0; right < size; right++)
{
// 进窗口
sum += nums[right];
// 判断
while(sum >= target)
{
// 更新结果,出窗口
len = min(len, right - left + 1);
sum -= nums[left++];
}
}
return len == INT_MAX ? 0 : len;
}
};