算法期末程序填空

news2024/9/20 9:44:11

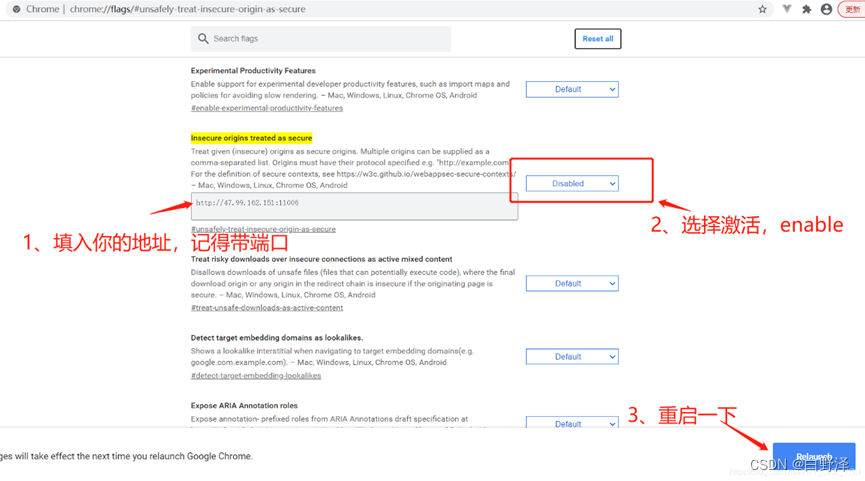
1.有重复元素全排列的计数问题(部分正确

【考察知识点】有重复元素的全排列的计数

【题目描述】

共有n个小球（1<=n<=20），这n个小球有k种颜色（1<=k<=10），白色s1​个，红色s2​个，……，蓝色sk​个，即n=s1​+s2​+…+sk​

现在将这n个小球进行排列，有多少种排列方式？

例如，有4个小球，其中2个白色，2个红色，则有以下6种排列：

白白红红

白红白红

白红红白

红白白红

红白红白

红红白白

【输入格式】

第一行，测试数据的组数，可输入多组测试数据，每一组测试数据都包含下面两行。

每组测试数据的第一行，n和k。n和k的描述和范围见前文描述。

每组测试数据的第二行，共k个数，s1​、s2​、…、sk​。见前文描述。

【输出格式】

共有多少种排列方式数。

【输入样例】

4 //表示4组测试数据

4 2 //第1组

2 2

5 3 //第2组

1 2 2

6 3 //第3组

2 2 2

10 4 //第4组

2 3 3 2

【输出样例】

(Test 1) Full permutations with repeating elements: 6

(Test 2) Full permutations with repeating elements: 30

(Test 3) Full permutations with repeating elements: 90

(Test 4) Full permutations with repeating elements: 25200

【样例程序】

#include "stdio.h"
#include <iostream>
#include "stdlib.h"
using namespace std;

//求阶乘
long long fact(int n)
{
    long long f=1;//2score
    for(int i=n; i>=1; i--)
        f*=i;  //累乘 3 score

    return f;
}

int main()
{
    int T ,t , n, k, s[11];
    cin >> T;
    t=T;
    while(T--)  //T为测试数据的组数，有几组
    {
        cin >> n >> k;
        for(int i=1;i<=k;i++) cin>>s[i];

        long long p=fact(n);
        for(int i=1;i<=k;i++) 
        divisor*=fact(s[i]);//3 score

        cout<<"(Test "<<t-T<<") "<<"Full permutations with repeating elements: "<< p <<endl;
    }
    return 0;
}

2.找零钱

【考察知识点】动态规划算法

【题目描述】
设有n种不同面值的钱币各若干张，可用这n种钱币产生许多不同的币值。
有零钱：{1元×3张，2元×3张，5元×1张}，若要找回7元，有如下4种方案：
（1）3张1元 + 2张2元
（2）1张1元 + 3张2元
（3）2张1元 + 1张5元
（4）1张2元 + 1张5元
这4种方案中，最少张数的方案为上面第（4）种方案，仅需2张。
你的任务：给定币值m和n种不同面值钱币及其张数，求要找回币值m最少要多少张。

【输入格式】
多组测试数据的形式。
第1行先输入有多少组测试数据，然后后续每组测试数据连续输入。
每组中的第1行有1个正整数n(1<=n<50)，表示有n种不同的钱币。
每组中的第2行有n个正整数，分别表示每种钱币的面值v[1]...v[n](0<=v[i]<=100, 1<=i<=n)。
每组中的第3行有n个正整数，分别表示每种钱币的张数k[1]...k[n] (0<=k[i]<=100, 1<=i<=n)。
每组中的第4行有1个正整数，表示给定需要找回的钱币值m (1<=m<=20000)。

【输出格式】
每组结果连续输出，每组输出占一行。
计算出给定币值所需的最少张数。
若无法给出找钱方案，返回“no possible”(注意：无大写且无标点)。

【输入样例】
1 （表示下面仅一组数据）
3
1 2 5
3 3 1
7

【输出样例】
2

#include <iostream>
#include "stdio.h"
#include "stdlib.h"
using namespace std;
#define MAX 100000

int c[51][20001];

int solve(int n, int *v, int *k, int m)
{
    int min=0x7fffffff,w,t;
    for(int i=0;i<=n;i++)
             c[i][0]=0;
    for(int j=0;j<=m;j++)
    {
        //c[ ][ ]第一行的填写
        if(j%v[1]==0 && j/v[1]<=k[1])
             c[1][j]=
j/v[1]
;
        else 
             c[1][j]=MAX;
    }

    //c[ ][ ]后续行的填写
    for(int i=2;i<=n;i++)
       for(int j=1;j<=m;j++)
       {
            t = (int)(j/v[i])>k[i]? k[i] : (int)(j/v[i]);
            min=c[i-1][j];
            for(int s=1;s<=
t
;s++)
            {
                if(j>=s*v[i])
                     w=
c[i-1][j - s * v[i]] + s
;
                else
                     w=MAX;
               if(w<min) min=w;
          }
          c[i][j]=min;
      }

     return 
c[n][m]
;   //返回哪个数组元素？
}

int main()
{
    int n;
    int v[51],k[51];
    int m;

    int T;
    scanf("%d", &T);  //共T组测试数据
    while(T--) { //逐组处理
        cin>>n;
        for(int i=1;i<=n;i++) cin>>v[i];
        for(int i=1;i<=n;i++) cin>>k[i];
        cin>>m;

        int q=solve(n,v,k,m);
        if(q!=MAX)
            cout<<q<<endl;
        else
            cout<<"no possible"<<endl;
     }

    return 0;
}

3.树状数组

【考察知识点】树状数组

【题目描述】
用树状数组高效实现区间求和操作。

注：本题要求用树状数组（即程序中的c[]）做区间求和，修改元素（addv函数）和前缀和求和（getSum函数）的时间复杂度都为O(logn)。用树状数组这一数据结构，比常规循环做前缀和要快的多。

【输入格式】
第1行先输入正整数n，表示数据元素的个数。元素个数n不超过100000。
第2行有n个整数，分别表示a[1]...a[n]的数值。
第3行有2个正整数，分别表示询问区间的左右边界。

【输出格式】
求询问区间的区间元素和。如样例数据中a[3]+a[4]+...+a[8]的和为33。

【输入样例】
10
1 2 3 4 5 6 7 8 9 10
3 8

【输出样例】
33

【样例程序】

#include <iostream>
#include <string.h>
#include "stdio.h"
#include "stdlib.h"
using namespace std;

int a[100001];  //输入数据
int c[100001];  //树状数组存储空间

int n;  //有效数据个数

//此函数为x二进制表达中最右边1与后面的全0（如果有的话），构成的数值。
//比如若x=12，二进制为1100，则lowbit(12)返回为4，二进制为100
int lowbit(int x) 
{
    return x&(-x);
}

//这个函数求a[1]+...+a[x]的和。指的是从1下标过来到下标x的元素和（称为前缀和）
int getSum(int x)  
{
    int ans = 0;
    while(x > 0){
        ans += 
c[x]
;
        x -= 
lowbit(x)
;
    }
    return ans;
}

//这个函数为a[x]做增值修改，即a[x]=a[x]+value后，树状数组c[ ]也随之做了相应的修改
void addv(int x, int value) 
{
    a[x] += value;
    while(x <= n){
        c[x] += 
value
;
        x += 
lowbit(x)
;
    }
}

int main()
{
    scanf("%d", &n);
    memset(a, 0, sizeof(a));
    memset(c, 0, sizeof(c));
    for(int v, i = 1; i <= n; i++) {
        scanf("%d", &v);
        addv(i, v);  //把输入值加到a[i]中，同时建立树状数组c[ ]
    }

    int l, r;
    scanf("%d%d", &l, &r);  //输入要获得区间和的区间左和右边界

    int ans=0;  //不合法输入都为0
    if (l>=1 && r<=n)
        if(l>1)
            ans = getSum(r)-getSum(l-1); //当左边界l>=2时，返回前缀和之差：即sum(r)-sum(l-1);
        else
            ans = getSum(r);   //当左边界l为1时，直接返回到r的前缀和(即sum(r)=a[1]+...+a[r])
    else {
        printf("Illegal data interval!");
    }

    printf("%d", ans);

    return 0;
}

4.亲戚关系

【考察知识点】并查集

【题目描述】
有亲戚关系的，可视为一个家族内。某些庞大的家族可能人数众多，要判断两个人是否是亲戚，确实还很不容易。

现在给出某个亲戚关系图，询问任意给出的两个人是否具有亲戚关系。

规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

【输入格式】
第一行：三个整数n, m, p，（范围：1<=n,m,p<=5000），分别表示有n个人，共列出m个亲戚关系，共询问p对人之间是否存在亲戚关系。
以下m行：每行两个数Mi​, Mj​（1<=Mi​,Mj​<=n），表示Mi​ 和Mj​ 具有亲戚关系，有m行这样的亲戚关系构成了家族图。
接下来p行：每行两个数Pi​, Pj​（1<=Pi​,Pj​<=n），询问Pi​ 和Pj​ 是否具有亲戚关系，有p次这样的询问。

【输出格式】
p行，每行一个’Yes’或’No’。表示第i个（1<=i<=p）的答案为“具有”或“不具有”亲戚关系。

这其实是一个很有现实意义的问题。我们可以建立并查集模型，把所有人划分到若干个不相交的集合中，每个集合里的人彼此是亲戚。为了判断两个人是否为亲戚，只需看它们是否属于同一个集合即可。因此，考虑用并查集进行维护所有的亲戚关系。

【输入样例】
11 7 8
1 3
2 3
5 6
9 10
5 10
4 9
8 11
1 3
2 8
6 8
3 9
4 6
5 9
4 5
9 11

【输出样例】
Yes
No
No
No
Yes
Yes
Yes
No

【样例程序】

#include <iostream>
#include "stdio.h"
#include "stdlib.h"
using namespace std;

#define MAXN 5001

//fa[i]记录i元素所属的集合代表元素
int fa[MAXN];
//rankhigh[]数组记录每个根节点对应的深度，如果它不是根节点，其rank值相当于以它作为根节点的子树的深度
int rankhigh[MAXN];

void init(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        fa[i] = 
i
;  //初始化时，所有元素的代表元素为自己本身
        rankhigh[i] = 1;  //初始化时，所有元素的秩为1
    }
}

//查找x属于哪个集合，返回这个集合的根代表
int find(int x)
{
    if(fa[x] != x)
        fa[x] = 
find(fa[x])
;  //查找x的fa[x]是谁？再继续递归地查找fa[fa[x]]又是谁？……
                //找完返回时，还顺便做个赋值，即路径压缩

    return fa[x];
}

//将i和j所在的集合进行合并
void merge(int i, int j)
{
    int x = find(i), y = find(j);
    //合并时比较两个根节点，把rank较小者往较大者上合并，可以不增加树高度
    if (rankhigh[x] <= rankhigh[y])
        fa[x] = 
y
;
    else
        fa[y] = 
x
;

    //如果深度相同且根节点不同，则新的根节点的深度+1
    if (rankhigh[x] == rankhigh[y] && x != y)
        rankhigh[y]++;
}

int main()
{
    int n, m, p, x, y;
    cin>>n>>m>>p;   //n个人，m个亲戚关系，p个询问亲戚关系
    init(n);
    for (int i = 0; i < m; ++i)  //m行，把具有亲戚关系的x和y给merge( )到一个家族中
    {
        cin>>x>>y;
        merge(x, y);
    }
    for (int i = 0; i < p; ++i)  //p个询问，若x和y是亲戚关系，则显示“Yes”，否则“No”
    {
        cin>>x>>y;
        if(find(x) == find(y))
            cout<<"Yes\n";
        else
            cout<<"No\n";
    }
    return 0;
}

5.两条线段的相交问题

【考察知识点】几何问题中的线段相交

【问题描述】

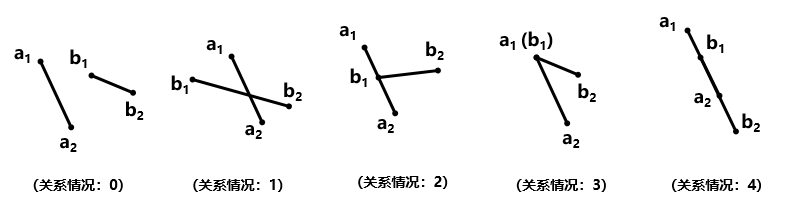
已知两条线段，线段端点由输入确定，先判定这两条线段的位置关系，存在如下五种关系：

0：两条线段无交点，不交叉或无公共点；

1：两条线段规范相交；

（此处先解释一下，何谓“规范相交”？ 规范相交规定为：两线段恰好有一个公共交点，且公共点不是任何线段的任何一个端点，也就是说，每条线段的两个端点都在另一条线段的两侧，我们可用叉积的异号来判断点是否在线段的两侧）

2：线段的某个端点在另一条线段上（不是另一条线段的端点，只是另一条线段中的某点）；

3：线段有唯一一个公共端点；

4：两条线段共线且有无数交点。

image.png

【输入格式】

先输入测试数据共有多少组。

每组分别输入两个线段的端点坐标（浮点型）：

a1.x a1.y a2.x a2.y

b1.x b1.y b2.x b2.y

【输出格式】

每组数据的结果按顺序输出。每组中，请输出两个线段的位置关系（用0~4数字表示情况）。如果是情况1，还需输出交叉的交点（保留2位小数形式）。其它情况无需输出交点。

【输入样例】

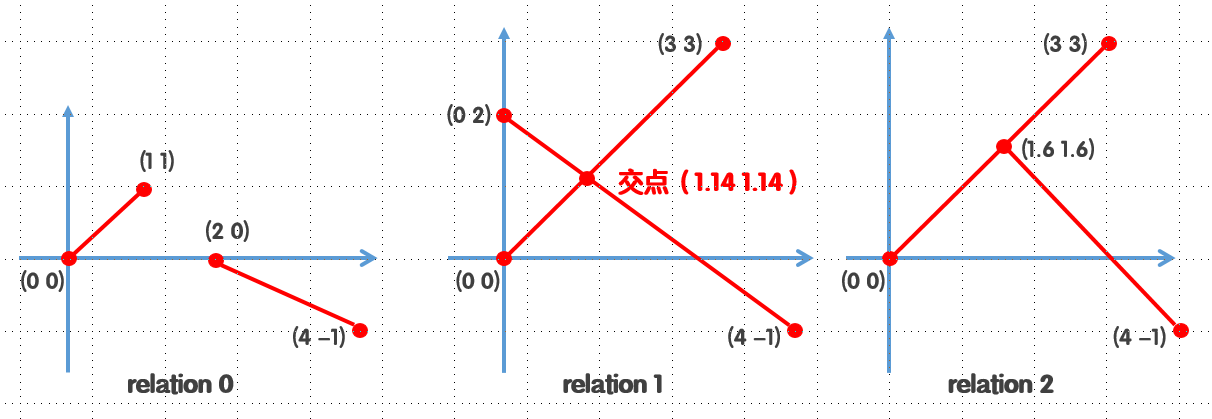
5 //共5组数据

0 0 1 1 //第1组

2 0 4 -1

0 0 3 3 //第2组

0 2 4 -1

0 0 3 3 //第3组

1.6 1.6 4 -1

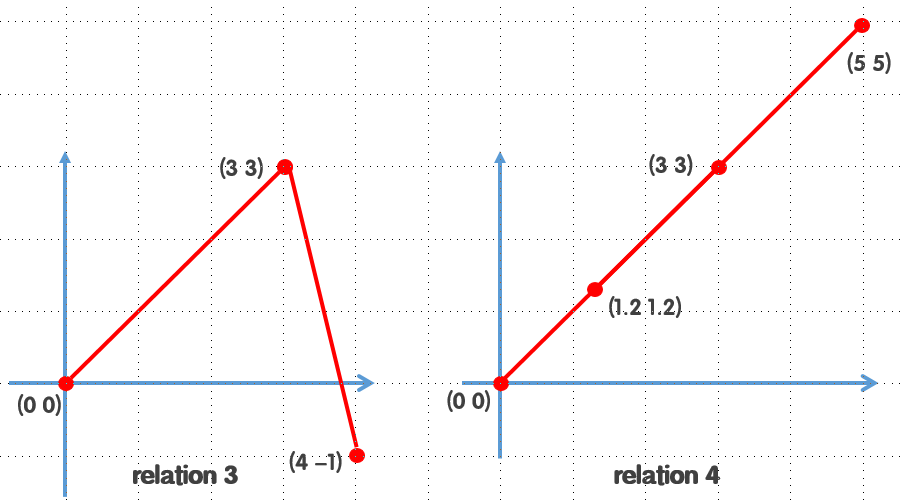
0 0 3 3 //第4组

3 3 4 -1

0 0 3 3 //第5组

1.2 1.2 5 5

【输出样例】

relation 0:

The two line segments: not intersect.

relation1:

The two line segments: proper intersect.

1.14 1.14

relation 2:

The two line segments: a end point is on the other segment.

relation 3:

The two line segments: a common point.

relation 4:

The two line segments: collinear.

【样例解释】

image.png

image.png

【样例程序】

#include "stdio.h"
#include <iostream>
#include "stdlib.h"
#include <cmath>

using namespace std;

//定义点
struct Point{
    double x;
    double y;
    Point(double x=0, double y=0):x(x), y(y) { }//构造函数，方便给x和y值的代码编写
};

//定义向量，向量和点的表示形式一样，但几何意义不同
typedef Point Vector;

// 向量+向量=向量，或者，向量+点=向量
Vector operator + (Vector A, Vector B) {return Vector(A.x+B.x, A.y+B.y);}

// 点-点=向量
Vector operator - (Point A, Point B) {return Vector(A.x-B.x, A.y-B.y);}

// 向量*数=向量，参数顺序：向量*浮点数，或浮点数*向量，两种参数顺序皆可乘
Vector operator * (Vector A, double p) {return Vector(A.x*p, A.y*p);}
Vector operator * (double p, Vector A) {return Vector(A.x*p, A.y*p);}

// 向量/数=向量
Vector operator / (Vector A, double p) {return Vector(A.x/p, A.y/p);}

//对double型的数，如何比较大于0，等于0，或小于0
const double EPS =1e-10;
int dcmp(double x)
{
    if (fabs(x)<EPS) return 0;
    else return x<0? -1 : 1;
}

//点积
double Dot(Vector A, Vector B) {return A.x*B.x + A.y*B.y;}
double Length(Vector A) {return sqrt(Dot(A,A));}

//叉积
double Cross(Vector A, Vector B) {return A.x*B.y - A.y*B.x;}

//判断p点是否在线段a1a2上，返回true的情况并不包括p恰好是线段端点（这种情况是返回false的）
int ontheSegment(Point p, Point a1, Point a2)
{
    return dcmp(Cross(a1-p, a2-p))==0 && dcmp(Dot(a1-p, a2-p))<0;
}

//定义五种位置关系的编号
const int NO_CROSSING_POINT = 0;
const int PROPER_INTERSECTION = 1;
const int ONE_POINT_ON_SEGMENT = 2;
const int COMMON_POINT = 3;
const int COLLINEAR = 4;

//判断两条线段的位置关系，是否“规范相交”
//规范相交定义为：两线段恰好有一个公共点，且公共点不是任何一条线段的端点
//判断是否规范相交，要做这样一个“跨立实验”的判断：每条线段的两个端点都在另一条线段的两侧
//“两侧”，可以用叉积的符号来判断
int judgeSegmentIntesection(Point a1, Point a2, Point b1, Point b2)
{
    //分别计算如下的c1、c2、c3、c4
    double c1=Cross(a2-a1,b1-a1);
    double c2=Cross(a2-a1,b2-a1);
    double c3=Cross(b2-b1,a1-b1);
    double c4=Cross(b2-b1,a2-b1);

    //线段a1a2和线段b1b2共线
    if(dcmp(c1)==0 && dcmp(c2)==0)
        return COLLINEAR;

    //有一个端点搭在另一条线段上，或共端点的情况
    if( ontheSegment(a1,b1,b2) || ontheSegment(a2,b1,b2) || ontheSegment(b1,a1,a2) || ontheSegment(b2,a1,a2))
        return ONE_POINT_ON_SEGMENT;
    else
        if((dcmp(c1)==0 && dcmp(c2) !=0) || (dcmp(c1)!=0 && dcmp(c2)==0) || (dcmp(c3)==0 && dcmp(c4)!=0) || (dcmp(c3)!=0 && dcmp(c4)==0))
            return ;

    //规范相交：c1和c2异号（点b1和点b2在线段a1a2的两侧），且c3和c4也异号（点a1和点a2在线段b1b2的两侧）
    if( dcmp(c1)*dcmp(c2)<0 &&  )
        return PROPER_INTERSECTION;
    else
        return NO_CROSSING_POINT;
}

//计算直线交点的坐标
Point GetSegmentIntersection(Point P, Vector v, Point Q, Vector w)
{
    Vector u=P-Q;
    double t = Cross(w,u)/Cross(v,w);
    return P+v*t;
}

int main()
{
    Point a1,a2,b1,b2;
    int T;

    cin>>T;  //T为测试数据的组数，共T组
    while(T--) {
        cin>>a1.x>>a1.y>>a2.x>>a2.y;  //输入线段的两个端点，即线段a1a2
        cin>>b1.x>>b1.y>>b2.x>>b2.y;  //输入线段的两个端点，即线段b1b2

        //先判断两条线段的位置关系
        int cas=judgeSegmentIntesection(a1, a2, b1, b2);
        cout<<"relation "<<cas<<":"<<endl;
        switch (cas)
        {
            case NO_CROSSING_POINT:
                cout<<"The two line segments: not intersect."<<endl; break;
            case PROPER_INTERSECTION:
                cout<<"The two line segments: proper intersect."<<endl; break;
            case ONE_POINT_ON_SEGMENT:
                cout<<"The two line segments: a end point is on the other segment."<<endl; break;
            case COMMON_POINT:
                cout<<"The two line segments: a common point."<<endl; break;
            case COLLINEAR:
                cout<<"The two line segments: collinear."<<endl; break;
            default:
                cout<<"error!"<<endl;
        }

        Point segmIntsectPoint;
        if (cas==PROPER_INTERSECTION)  //若规范相交，则计算交点坐标
        {
            segmIntsectPoint=GetSegmentIntersection(a1, , b1, b2-b1);
            printf("%.2f %.2f\n", segmIntsectPoint.x, );
        }
    }
    return 0;
}

 

部分正确

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1907629.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

大模型时代的蓝海任务，GPT4V准确率不足10%，港科大发布指代理解基准RefCOCO

大模型时代的蓝海任务，GPT4V准确率不足10%，港科大发布指代理解基准RefCOCO

谈到多模态大模型的应用场景&#xff0c;除了生成任务以外&#xff0c;应用最广泛的可能就是在图像和视频中进行目标检测。 目标检测要求从图像中识别并标注出所有感兴趣的对象&#xff0c;并给每个对象分配一个类别标签。典型的目标检测方法会生成边界框&#xff0c;标记出图…
阅读更多...
百度、谷歌、必应收录个人博客网站

百度、谷歌、必应收录个人博客网站

主要是给各个搜索引擎提交你的sitemap文件&#xff0c;让别人能搜到你博客的内容。 主题使用的Butterfly。 生成sitemap 安装自动生成sitemap插件。 npm install hexo-generator-sitemap --save npm install hexo-generator-baidu-sitemap --save在站点配置文件_config.yml…
阅读更多...
LabVIEW高能质子束流密度分布测试系统

LabVIEW高能质子束流密度分布测试系统

LabVIEW平台开发的高能质子束流密度分布测试系统。该系统主要应用于电子器件的抗辐射加固试验&#xff0c;旨在精确测量高能质子束的密度分布&#xff0c;以评估电子器件在辐射环境下的性能表现和耐受能力。 系统组成与设计 硬件组成&#xff1a; 法拉第杯探测器&#xff1a;…
阅读更多...
C++ 类和对象 拷贝构造函数

C++ 类和对象 拷贝构造函数

一 拷贝构造函数的概念&#xff1a; 拷贝构造函数是一种特殊的构造函数&#xff0c;用于创建一个对象是另一个对象的副本。当需要用一个已存在的对象来初始化一个新对象时&#xff0c;或者将对象传递给函数或从函数返回对象时&#xff0c;会调用拷贝构造函数。 二 拷贝构造函…
阅读更多...
静态路由配置注意事项及黑洞路由的使用

静态路由配置注意事项及黑洞路由的使用

静态路由 1 . 定义 从管理员处学习到的数据转发路径&#xff0c;就称为静态路由。 2 . 路由表 Proto &#xff1a;协议&#xff08; Protocol &#xff09; Direct — 直连链路Static — 静态路由RIP 、OSPF 等 — 动态路由 Pre : 优先级&#xff08; Preference &#x…
阅读更多...
ozon跨境电商可以做吗，俄罗斯ozon跨境电商可不可以做

ozon跨境电商可以做吗，俄罗斯ozon跨境电商可不可以做

当今全球化的浪潮下&#xff0c;跨境电商已成为连接世界各地消费者与商家的桥梁&#xff0c;为无数企业开辟了全新的市场蓝海。俄罗斯&#xff0c;作为世界上最大的国家之一&#xff0c;其电商市场近年来蓬勃发展&#xff0c;尤其是ozon平台&#xff0c;作为俄罗斯本土的电商巨…
阅读更多...
你真的会信息收集嘛，4k字渗透测试信息收集10大技巧

你真的会信息收集嘛，4k字渗透测试信息收集10大技巧

前言 在渗透测试中&#xff0c;信息收集是非常关键的一步&#xff0c;它为后续的漏洞发现和利用提供了重要的基础。以下是非常详细的信息收集方式&#xff1a; 一、被动信息收集 被动信息收集是指在不与目标系统直接交互的情况下&#xff0c;通过公开渠道获取目标系统的相关…
阅读更多...
Redhat 安装 docker 网络连接超时问题

Redhat 安装 docker 网络连接超时问题

目录 添加阿里云的Docker CE仓库 更新YUM缓存 安装 Docker Engine 启动并设置Docker自启动 验证 Docker 安装 [userlocalhost ~]$ sudo yum-config-manager --add-repohttps://download.docker.com/linux/centos/docker-ce.repo 正在更新 Subscription Management 软件仓库…
阅读更多...
高考志愿填报的六个不要

高考志愿填报的六个不要

在高考志愿填报这个关键时刻&#xff0c;确实需要谨慎行事&#xff0c;避免一些常见的错误。以下是高考志愿填报的六个“不要”&#xff0c;希望能为你提供一些有用的建议&#xff1a; 1、不要盲目跟风 每个人的兴趣、能力和未来规划都不同&#xff0c;不要仅仅因为某个专业或…
阅读更多...
202406 CCF-GESP Python 三级试题及详细答案注释

202406 CCF-GESP Python 三级试题及详细答案注释

202406 CCF-GESP Python 三级试题及详细答案注释 1 单选题（每题 2 分，共 30 分）第 1 题 小杨父母带他到某培训机构给他报名参加CCF组织的GESP认证考试的第1级，那他可以选择的认证语言有几种？（ ） A. 1 B. 2 C. 3 D. 4答案：C解析：目前CCF组织的GESP认证考试有C++、Pyth…
阅读更多...
LVS+Nginx高可用集群---Nginx进阶与实战

LVS+Nginx高可用集群---Nginx进阶与实战

1.Nginx中解决跨域问题 两个站点的域名不一样&#xff0c;就会有一个跨域问题。 跨域问题&#xff1a;了解同源策略&#xff1a;协议&#xff0c;域名&#xff0c;端口号都相同&#xff0c;只要有一个不相同那么就是非同源。 CORS全称Cross-Origin Resource Sharing&#xff…
阅读更多...
Vue+ElementUi实现录音播放上传及处理getUserMedia报错问题

Vue+ElementUi实现录音播放上传及处理getUserMedia报错问题

1.Vue安装插件 npm install --registryhttps://registry.npmmirror.com 2.Vue页面使用 <template><div class"app-container"><!-- header --><el-header class"procedureHeader" style"height: 20px;"><el-divid…
阅读更多...
AJAX快速入门(一) express框架的安装和使用范例

AJAX快速入门(一) express框架的安装和使用范例

主打一个有用 首先保证安装了nodejs环境 打开终端 初始化npm npm init安装express npm i express测试样例 目录结构 样例代码 express.js //引入express const express require(express);//创建应用对象 const app express();//创建路由规则 //req是请求对象&#x…
阅读更多...
C#委托事件的实现

C#委托事件的实现

1、事件 在C#中事件是一种特殊的委托类型&#xff0c;用于在对象之间提供一种基于观察者模式的通知机制。 1.1、事件的发送方定义了一个委托&#xff0c;委托类型的声明包含了事件的签名&#xff0c;即事件处理器方法的签名。 1.2、事件的订阅者可以通过运算符来注册事件处理器…
阅读更多...
HTTP 请求走私漏洞详解

HTTP 请求走私漏洞详解

超详细的HTTP请求走私漏洞教程&#xff0c;看完还不会你来找我。 1. 简介 HTTP请求走私漏洞&#xff08;HTTP Request Smuggling&#xff09;发生在前端服务器&#xff08;也称代理服务器&#xff0c;一般会进行身份验证或访问控制&#xff09;和后端服务器在解析HTTP请求时&…
阅读更多...
【GIt】变基(rebase)

【GIt】变基(rebase)

目录 变基(rebase)是什么为什么有变基变基后的时间线变基前的时间线 变基原理怎么变基同一个分支变基不同分支变基 参考文章 变基(rebase)是什么 Git 变基&#xff08;rebase&#xff09;是一种用于整合分支的方法&#xff0c;它的工作原理是将一系列提交&#xff08;或分支合…
阅读更多...
太实用了吧？手把手教你华为eNSP模拟器桥接真实网络！

太实用了吧？手把手教你华为eNSP模拟器桥接真实网络！

号主&#xff1a;老杨丨11年资深网络工程师&#xff0c;更多网工提升干货&#xff0c;请关注公众号&#xff1a;网络工程师俱乐部 晚上好&#xff0c;我的网工朋友。 今天聊聊eNSP桥接正式网络&#xff0c;就是把eNSP桥接进真实的网络&#xff0c;利用我们的物理网卡通过实体路…
阅读更多...
MoonBit 周报 Vol.48：默认开启诊断信息渲染、test block 不再返回 Result 类型的结果

MoonBit 周报 Vol.48：默认开启诊断信息渲染、test block 不再返回 Result 类型的结果

weekly 2024-07-08 MoonBit 更新 【重大更新】修改 array slice 的语法&#xff0c;从 arr[start..end] 修改为类似 Python 的 arr[start:end]。这是为了避免和接下来要支持的 cascade method call x..f() 产生语法冲突。旧的语法会在近期删除。 【Wasm后端重大更新】将 fn i…
阅读更多...
什么是C#

什么是C#

C#是一种面向对象的语言与c语言不同 C语言是面向过程的编程 C#运行于.NETFramework和.NETCore之上的高级语言 C#是由C和C衍生而来的一种语言 在C#中不建议使用指针 什么叫面向对象 是一种编程范式&#xff0c;它将现实世界中的事物抽象为对象&#xff0c;并通过对象之间的…
阅读更多...
田地行走-美团2023笔试(codefun2000)

田地行走-美团2023笔试(codefun2000)

题目链接 田地行走-美团2023笔试(codefun2000) 题目内容 塔子哥是一个农民&#xff0c;他有一片 nm 大小的田地&#xff0c;共 n 行 m 列&#xff0c;其中行和列都用从 1 开始的整数编号&#xff0c;田地中有 k 个格子中埋有土豆。我们记第 a 行第 b 列的格子为 (a,b) 。塔子哥…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023