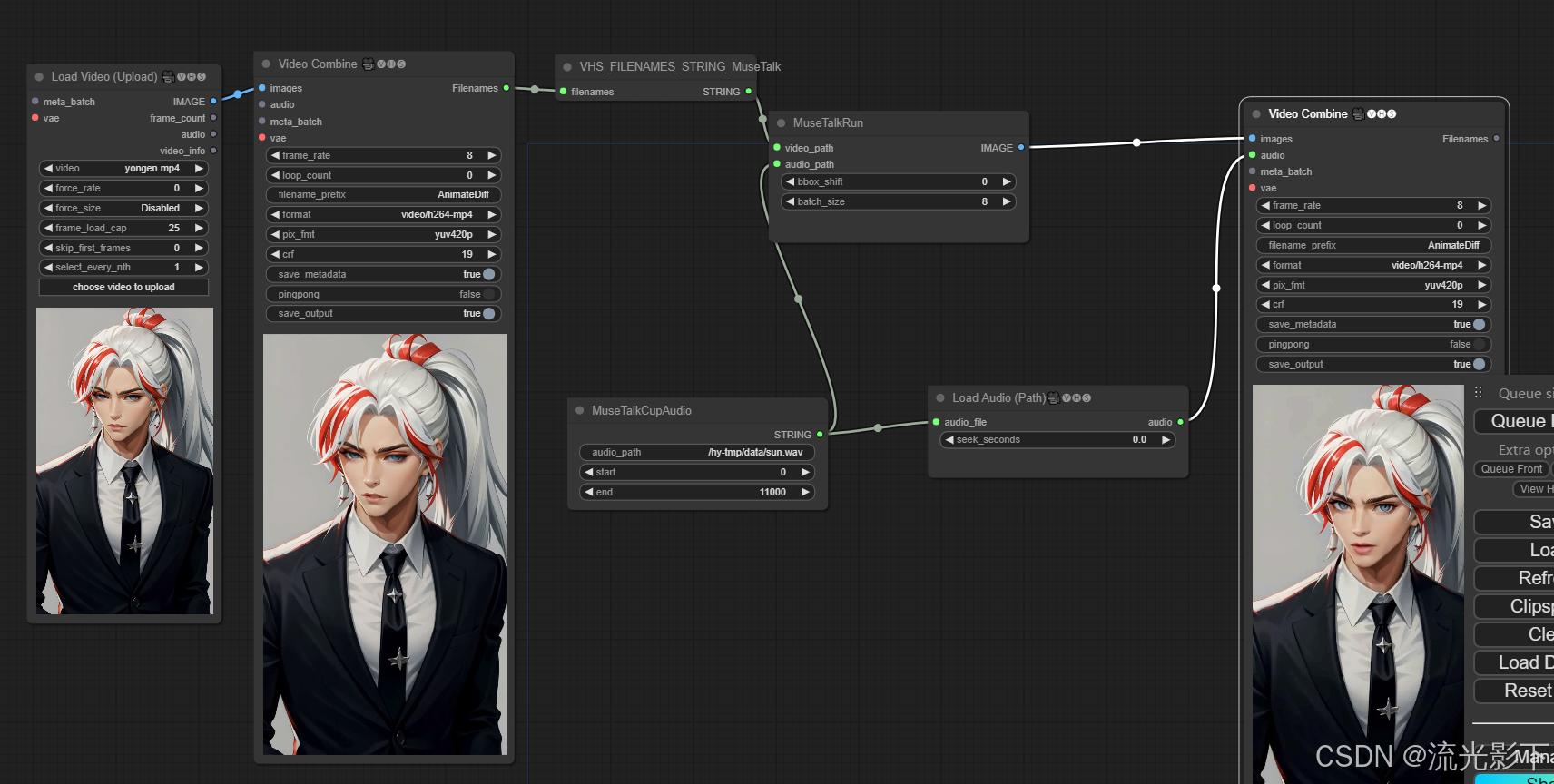
长参数“T”决定了生成全噪声图像所需的步长。在本文中,该参数被设置为1000,这可能显得很大。我们真的需要为数据集中的每个原始图像创建1000个噪声图像吗?马尔可夫链方面被证明有助于解决这个问题。由于我们只需要上一步的图像来预测下一步,并且每一步添加的噪声保持不变,因此我们可以通过生成特定时间戳的噪声图像来简化计算;
这段话主要解释了在使用扩散模型生成全噪声图像时,所需的步长参数“T”的意义,以及如何通过马尔可夫链简化计算。以下是对这段话的详细解释:
步长参数“T”
-
步长参数“T”:
- 定义:步长参数“T”决定了生成全噪声图像所需的总步骤数。
- 在本文中的设置:在这篇文章中,T 被设置为1000。这意味着生成一个完全噪声化的图像需要经过1000个步骤。
-
是否需要1000个噪声图像:
- 疑问:我们真的需要为数据集中的每个原始图像创建1000个不同的噪声图像吗?
- 答案:不一定需要这么多。虽然T被设置为1000,但并不意味着我们必须生成1000个噪声图像。
马尔可夫链
-
马尔可夫链的帮助:
- 定义:马尔可夫链是一种随机过程,当前状态只依赖于前一个状态,而与更早的状态无关。
- 应用:在扩散模型中,图像的每一步状态只依赖于上一步的状态。这意味着我们不需要保存所有的中间步骤。
-
简化计算:
- 只需要上一步的图像:由于我们只需要前一步的图像来预测下一步,并且每一步添加的噪声保持不变,因此我们可以简化计算。
- 生成特定时间戳的噪声图像:通过直接生成特定时间戳的噪声图像,我们可以避免创建所有的中间步骤图像。例如,如果我们需要第500步的图像,我们可以直接从第499步的图像生成,而不需要从第1步开始生成所有图像。
具体解释
-
参数“T”设置为1000的含义:
- 设置T为1000意味着我们假定需要1000步才能从原始图像逐渐过渡到完全噪声化的图像。这是为了确保噪声逐步添加,并且每一步的变化足够小,使得逆过程可以更好地学习如何还原图像。
-
马尔可夫链的性质:
- 马尔可夫链的性质允许我们只关注当前和前一步的状态。这意味着在任何一步t,我们只需要知道第t-1步的状态,就可以计算出第t步的状态。
-
计算的简化:
- 由于每一步的噪声添加保持不变,我们可以通过直接生成某一步(如第500步)的噪声图像,而不需要依次生成每一步的图像。这大大简化了计算过程。
示例
假设我们要生成一个特定时间步t的噪声图像:
- 传统方法:我们从第0步开始,每一步添加噪声,直到生成第t步的图像。这需要计算t次。
- 简化方法:由于每一步只依赖前一步,并且噪声添加保持不变,我们可以直接从第t-1步的图像生成第t步的图像。这只需要一步计算。
总结
设置步长参数T为1000看起来很大,但实际上通过使用马尔可夫链的性质,我们可以简化计算,只需要生成特定时间步的噪声图像,而不需要每一步都计算所有中间状态。这使得生成噪声图像的过程更加高效和简便。
在扩散模型中,第499步的图像是通过前一步(第498步)的图像生成的,而第498步的图像是通过第497步的图像生成的,以此类推。这种逐步生成的方法依赖于马尔可夫链的性质,即每一步的状态只依赖于前一步的状态。
不过,如果我们只关心第499步的图像,我们不需要依次生成每一步的图像。相反,我们可以利用扩散模型的公式和噪声添加过程来直接生成特定时间步的图像。这里是一个更详细的解释:
逐步生成的过程
- 正向过程(Forward Process):从原始图像逐步添加噪声直到完全变成噪声图像。

其中,αt 是时间步 t的系数,x0是原始图像,ϵ 是从标准正态分布采样的噪声。
直接生成特定时间步的图像
我们可以使用正向过程的公式来直接生成特定时间步(如第499步)的图像。具体步骤如下: