1.题目描述
给你一个二维字符矩阵
grid,其中grid[i][j]可能是'X'、'Y'或'.',返回满足以下条件的子矩阵数量:
- 包含
grid[0][0]'X'和'Y'的频数相等。- 至少包含一个
'X'。示例 1:
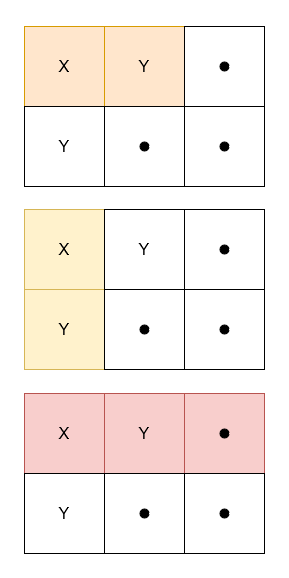
输入: grid = [["X","Y","."],["Y",".","."]]
输出: 3
解释:
示例 2:
输入: grid = [["X","X"],["X","Y"]]
输出: 0
解释:
不存在满足
'X'和'Y'频数相等的子矩阵。
2.解题思路
拿到这题首先可以想到使用dp数组存储以每一个点为结束位置的子矩阵中的X,Y个数,可以看出对于下标[i,j],假设i,j均>=1,那么dp[i][j]对应矩阵的X,Y个数是可以通过dp[i-1][j],dp[i][j-1]以及dp[i-1][j-1]这三个子矩阵进行加减操作得到的。
因此,为了表示每个以i,j为结束位置的子矩阵中"X"和“Y”各自的个数,我们定义一个三维dp数组,dp[i][j][0]用于记录"X"的个数,dp[i][j][1]用于记录“Y”的个数,接下来只需要先初始化第0行和第0列这两种特殊情况,然后一般情况就可以通过递推式进行判断
3.代码实现
Java版
class Solution {
public int numberOfSubmatrices(char[][] grid) {
int m = grid.length, n = grid[0].length;
int[][][] dp = new int[m][n][2];
if (grid[0][0] == 'X') {
dp[0][0][0] += 1;
} else if (grid[0][0] == 'Y') {
dp[0][0][1] += 1;
}
int ans = 0;
//初始化第0行
for (int j = 1; j < n; j++) {
int x = dp[0][j-1][0];
int y = dp[0][j-1][1];
if (grid[0][j] == 'X') {
x += 1;
} else if (grid[0][j] == 'Y') {
y += 1;
}
dp[0][j][0] = x;
dp[0][j][1] = y;
if (dp[0][j][0] >= 1 && dp[0][j][0] == dp[0][j][1]) {
ans += 1;
}
}
//初始化第0列
for (int i = 1; i < m; i++) {
int x = dp[i-1][0][0];
int y = dp[i-1][0][1];
if (grid[i][0] == 'X') {
x += 1;
} else if (grid[i][0] == 'Y') {
y += 1;
}
dp[i][0][0] = x;
dp[i][0][1] = y;
if (dp[i][0][0] >= 1 && dp[i][0][0] == dp[i][0][1]) {
ans += 1;
}
}
//遍历
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
int x = dp[i-1][j][0] + dp[i][j-1][0] - dp[i-1][j-1][0];
int y = dp[i-1][j][1] + dp[i][j-1][1] - dp[i-1][j-1][1];
if (grid[i][j] == 'X') {
x += 1;
} else if (grid[i][j] == 'Y') {
y += 1;
}
dp[i][j][0] = x;
dp[i][j][1] = y;
if (dp[i][j][0] >= 1 && dp[i][j][0] == dp[i][j][1]) {
ans += 1;
}
}
}
return ans;
}
}Python版
class Solution:
def numberOfSubmatrices(self, grid: List[List[str]]) -> int:
m,n = len(grid),len(grid[0])
ans = 0
dp = [[[0,0] for _ in range(n)] for _ in range(m)]
if grid[0][0] == 'X':
dp[0][0] = [1,0]
elif grid[0][0] == 'Y':
dp[0][0] = [0,1]
#初始化第0行
for j in range(1,n):
if grid[0][j] == 'X':
dp[0][j] = [dp[0][j-1][0] + 1,dp[0][j-1][1]]
elif grid[0][j] == 'Y':
dp[0][j] = [dp[0][j-1][0],dp[0][j-1][1] + 1]
else:
dp[0][j] = dp[0][j-1]
if dp[0][j][0] >= 1 and dp[0][j][0] == dp[0][j][1]:
ans += 1
#初始化第0列
for i in range(1,m):
if grid[i][0] == 'X':
dp[i][0] = [dp[i-1][0][0] + 1,dp[i-1][0][1]]
elif grid[i][0] == 'Y':
dp[i][0] = [dp[i-1][0][0],dp[i-1][0][1] + 1]
else:
dp[i][0] = dp[i-1][0]
if dp[i][0][0] >= 1 and dp[i][0][0] == dp[i][0][1]:
ans += 1
for i in range(1,m):
for j in range(1,n):
x = dp[i-1][j][0] + dp[i][j-1][0] - dp[i-1][j-1][0]
y = dp[i-1][j][1] + dp[i][j-1][1] - dp[i-1][j-1][1]
if grid[i][j] == 'X':
dp[i][j] = [x+1,y]
elif grid[i][j] == 'Y':
dp[i][j] = [x,y+1]
else:
dp[i][j] = [x,y]
if dp[i][j][0] >= 1 and dp[i][j][0] == dp[i][j][1]:
ans += 1
return ans