模板
int check() {...} // 检查这个数是否符合相应的要求
// 把区间[l, r] 划分成[l, mid] 和 [mid+1, r] 时使用
// 找到数组中第一个大于等于某一值得元素或满足特定条件的第一个位置
int bsearch_1(int l, int r){
int mid = l + r >> 1;
while(l < r) {
if(check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
// 把区间[l, r] 划分成[l, mid-1] 和 [mid, r] 时使用、
// 找到数组中最后一个不大于某一值得元素或满足特定条件的最后一个位置
int bsearch_2(int l, int r){
int mid = l + r + 1 >> 1;
while(l < r){
if(check(mid) l = mid;
else r = mid - 1;
}
return l;
}
模板1计算mid没有偏移。此时如果check(mid)为真,说明mid位置的元素满足条件,我们不希望直接返回,我们希望找到最左边的。因此,我们将右边界r更新为mid,即缩小搜索区间到[l, mid],继续在左侧寻找。
模板2计算mid在偶数长度区间没有影响,在奇数长度区间,向右偏移。即使当mid位置的元素满足条件,我们也不会立刻排除其右侧可能存在的更多满足条件的元素,通过将l更新为mid,我们保留了右侧的搜索空间,直到最终确定最右侧的满足条件元素。
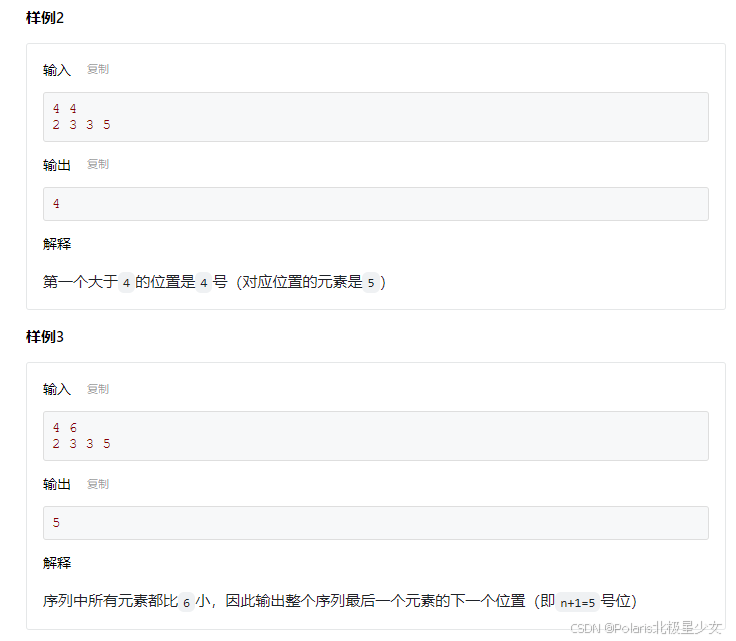
1.789. 数的范围 - AcWing题库
 、
、
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int q[N];
int main(){
int m, n, a;
cin >> n >> m;
for(int i = 0; i < n; i++){
cin >> q[i];
}
while(m--){
cin >> a;
int l = 0, r = n - 1;
// 找第一个
while(l < r){
int mid = l + r >> 1;
if(q[mid] >= a) r = mid;
else l = mid + 1;
}
// 没有找到
if(q[l] != a)
cout << "-1 -1" << endl;
else{
cout << l << " ";
// 找最后一个
int l = 0, r = n - 1;
while(l < r){
int mid = l + r + 1 >> 1;
if(q[mid] <= a) l = mid;
else r = mid - 1;
}
cout << l << endl;
}
}
return 0;
}
2.790. 数的三次方根 - AcWing题库

#include<iostream>
#include<iomanip>
using namespace std;
int main(){
double x;
cin >> x;
// 题目所给的范围
double l = -10000, r = 10000;
// 精度规定
while(r - l > 1e-8){
double mid = (l + r) / 2;
// 满足要求 继续向左找
if(mid * mid * mid >= x) r = mid;
else l = mid;
}
cout << fixed << setprecision(6) << l << endl;
return 0;
}cout 的精度是6
下面这种是指精度为n,不是小数点后的
cout << setprecision(n)
下面这种是指小数点后的精度为(n)
cout << fixed << setprecision(n)
浮点数二分模板:
bool check() { ... } // 检查该数字是否满足某一性质
int bsearch_3(double l, double r){
const double eps = 1e-6; // eps表精度 取决于题目的要求
while(r - l > eps){
double mid = (l + r) / 2;
if(chech(mid)) r = mid;
else l = mid;
}
return l;
}