数据结构实验三: 图的操作与实现

news2024/9/20 8:52:05

数据结构实验一:线性表,堆栈和队列实现
数据结构实验二 :二叉树的操作与实现
数据结构实验三: 图的操作与实现
数据结构实验四 : 查找和排序算法实现

文章目录

  • 一、实验目的：
  • 二、使用仪器、器材
  • 三、实验内容及原理
    • 1、教材P310实验题1：实现图的邻接矩阵和邻接表的存储
    • 2、教材P310实验题2：实现图的遍历算法
    • 3、教材P311实验题5：采用Prim算法求最小生成树
    • 4、教材P311实验题10：求有向图的简单路径
    • 5、教材P313实验题14：用图搜索方法求解如图3.28（教材P119）的迷宫问题（也可以自建迷宫）

一、实验目的：

1、领会图的两种主要存储结构和图的基本运算算法设计；
2、领会图的两种遍历算法；
3、领会Prim算法求带权连通图中最小生成树的过程和相关算法设计；
4、掌握深度优先遍历和广度优先遍历算法在图路径搜索问题中的应用；
5、深入掌握图遍历算法在求解实际问题中的应用。

二、使用仪器、器材

微机一台
操作系统：WinXP
编程软件：C/C++编程软件

三、实验内容及原理

1、教材P310实验题1：实现图的邻接矩阵和邻接表的存储

编写一个程序graph.cpp，设计带权图的邻接矩阵与邻接表的创建和输出运算，并在此基础上设计一个主程序exp8-1.cpp完成以下功能。
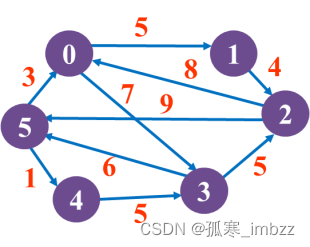
（1）建立如图8.54所示的有向图G的邻接矩阵，并输出之。
（2）建立如图8.54所示的有向图G的邻接表，并输出之。
（3）销毁图G的邻接表。

图8.54 一个带权有向图

#include <iostream>
#include<iomanip>
using namespace std;
#define maxn 1024   //最大顶点数
int matrix[maxn][maxn];   //邻接矩阵
int n, m; //顶点数，边数
/*
边结点
*/
struct ArcNode {
    int adjvex;  //该边所指向的顶点的位置
    int lowcost; //权值
    ArcNode* next;  //指向的下一条边的指针
};

ArcNode* ArcList[maxn * (maxn - 1)];   //所有边结点
int in = 0;   //下标

/*
顶点
*/
struct {
    ArcNode* firstarc;
}AdjList[maxn];

/*
增加一条从i指向j的权值为k的顶点
*/
void add(int i, int j, int k) {
    matrix[i][j] = k;
    ArcNode* p = new ArcNode();
    p->adjvex = j;  //它指向的是j顶点
    p->lowcost = k; //权值为k
    //p插入到链表头部
    p->next = AdjList[i].firstarc;
    AdjList[i].firstarc = p;
    ArcList[in++] = p;  //把这个边结点存储到数组中,顺便完成遍历
}


int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    n = 6;
    m = 10;
    //初始化邻接矩阵
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            matrix[i][j] = -1;
        }
    }
    //初始化AdjList
    for (int i = 0; i < n; ++i) {
        AdjList[i].firstarc = NULL;
    }
    //增加m条边
    add(0, 1, 5);
    add(0, 3, 3);
    add(1, 2, 4);
    add(2, 0, 8);
    add(2, 5, 9);
    add(3, 2, 5);
    add(3, 5, 6);
    add(4, 3, 5);
    add(5, 4, 1);
    add(5, 0, 3);
    //打印邻接矩阵
    cout << "adjacent matrix:" << endl;
    for (int i = 0; i < n; ++i) {
        cout << i << " :";
        for (int j = 0; j < n; ++j) {
            cout << setw(5)<<matrix[i][j] ;
        }
        cout << endl;
    }
    //打印邻接表
    cout << "adjacency list:" << endl;
    ArcNode* p = 0;
    for (int i = 0; i < n; ++i) {
        p = AdjList[i].firstarc;
        cout << i << " : ";
        while (p) {
            cout << p->adjvex << "(" << p->lowcost << ")" << " -> ";
            p = p->next;
        }
        cout << "^" << endl;
    }
    p = 0;
    //销毁邻接表
    for (int i = 0; i < in; ++i) {
        delete ArcList[i];  //删除
        ArcList[i] = 0;  //指针置空
    }
    //修改每个顶点的firstarc为空
    for (int i = 0; i < n; ++i) {
        AdjList[i].firstarc = 0;
    }
    in = 0;
    return 0;
}

2、教材P310实验题2：实现图的遍历算法

编写一个程序travsal.cpp实现图的两种遍历运算，并在此基础上设计一个程序exp8-2.cpp完成以下功能。
（1）输出如图8.54的有向图G从顶点0开始的深度优先遍历序列（递归算法）。
（2）输出如图8.54的有向图G从顶点0开始的深度优先遍历算法（非递归算法）。
（3）输出如图8.54的有向图G从顶点0开始的广度优先遍历序列。

#include<iostream>
#include<vector>
using namespace std;
#define maxn 128

//标记数组 标记是否被访问
int tag[maxn];

//带权节点 用数组表示
struct edgeNode {
	int value;
	int valueOfLine;
	edgeNode* next;
	edgeNode(int v, int V) {
		this->value = v;
		this->valueOfLine = V;
		this->next = NULL;
	}
};
//节点链表
struct Vl {
	edgeNode * first;
}VList[maxn];

//插入链表 连接节点
void Link(int i, int j, int value) {
	edgeNode* p = new edgeNode(j, value);
	p->next = VList[i].first;
	VList[i].first = p;
}

//深度优先 递归
void DFS(int i = 0) {
	tag[i] = 1;
	edgeNode* temp = VList[i].first;
	cout << temp->value << "  ";
	while (temp) {
		if (tag[temp->value] != 1) {
			DFS(temp->value);
		}
		temp = temp->next;
	}
}

/*
* 深度优先 非递归
*/

int stk[maxn]; //模拟栈
int stkSum;//栈的元素个数
//非递归
void DFS2() {
	memset(tag, 0, sizeof(tag));  //清空访问标记
	//当前顶点
	int v = 0;
	//栈元素
	stkSum = 0;
	tag[v] = 1;//标记
	stk[stkSum++] = v;//入栈
	cout << "深度优先 非递归:" ;
	edgeNode* temp = NULL;//取第一个元素
	while (stkSum) {
		//只要栈不空 说明没有遍历完 继续
		v = stk[--stkSum];//出栈栈顶
		cout << v << " ";//出栈输出
		temp = VList[v].first;
		while (temp) {
			if (!tag[temp->value]) {
				//如果没有访问过
				tag[temp->value] = 1;//标记
				stk[stkSum++] = temp->value;//入栈
			}
			temp = temp->next;//遍历
		}
	}
	cout << endl;
}

/*
* 广度优先
*/
//模拟队列
int quen[maxn];
//左右指针  int left = 0,int right=0
void BFS(int v = 0, int left = 0, int right = 0) {
	//标记0
	memset(tag, 0, sizeof(tag));  //清空访问标记
	tag[v] = 1;  //标记初始顶点
	cout << "bfs:";
	quen[right++] = v;   //入队
	edgeNode* p = 0;
	while (left != right) {
		//只要队列不空，就一直循环
		v = quen[left++];  //出队
		cout << v << "  "; //输出顶点
		left %= maxn; //如果qi >= maxn，则从0开始
		p = VList[v].first;
		while (p) {
			if (!tag[p->value]) {
				//只要没被访问过就入栈
				quen[right++] = p->value;
				right %= maxn;
				tag[p->value] = 1;  //标记
			}
			p = p->next;  //指针后移
		}
		p = 0;  //指针置空
	}
}

/*
	销毁邻接表
*/
void destoryArc(int n) {
	//销毁邻接表
	for (int i = 0; i < n; i++) {
		while (VList[i].first) {
			edgeNode* head = VList[i].first;
			VList[i].first = head->next;
			delete head;
		}
	}
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int v = 6;
	int L = 10;
	//初始化AdjList
	for (int i = 0; i < v; ++i) {
		VList[i].first = NULL;
	}
	//增加m条边
	Link(0, 1, 5);
	Link(0, 3, 3);
	Link(1, 2, 4);
	Link(2, 0, 8);
	Link(2, 5, 9);
	Link(3, 2, 5);
	Link(3, 5, 6);
	Link(4, 3, 5);
	Link(5, 4, 1);
	Link(5, 0, 3);
	//-----------深度优先（递归）----------
	memset(tag, 0, sizeof(tag));  //清空访问标记
	cout << "dfs(recursion):";
	DFS();
	cout << endl;
	memset(tag, 0, sizeof(tag));  //清空访问标记
	//-----------深度优先（非递归）----------
	DFS2();
	//-----------广度优先----------
	BFS();
	cout << endl;
	destoryArc(6);  //销毁邻接表
	return 0;

}

3、教材P311实验题5：采用Prim算法求最小生成树

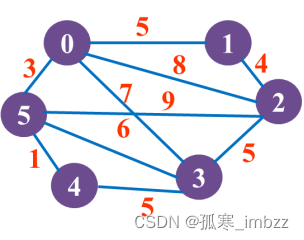
编写一个程序exp8-5.cpp，实现求带权连通图中最小生成树的Prim算法，如图8.55所示的带权连通图G，输出从顶点0出发的一棵最小生成树。

图8.55 一个带权连通图

#include <iostream>
using namespace std;
typedef long long ll;
# define maxn 1024    //最大顶点数量
int matrix[maxn][maxn];   //邻接矩阵
bool tag[maxn];   //标记，tag[i]=1表示顶点i在集合U中
int n, m;  //n:顶点个数（其中顶点标号从1到n）  m：边的个数
struct {
	int adjvex;  //最小边在U中的那个顶点
	int lowcost;  //最小边上的权值
}closedge[maxn];

/*
增加一条连接n1顶点和n2顶点的边，权值为k
*/
void link(int n1, int n2, int k) {
	matrix[n1][n2] = k;
	matrix[n2][n1] = k;
}

/*
初始化
*/
void init() {
	//初始化邻接矩阵
	for (int i = 0; i < maxn; ++i) {
		for (int j = 0; j < maxn; ++j) {
			matrix[i][j] = -1;
		}
	}
	memset(tag, 0, sizeof(maxn));
	n = 6;   //一共有6个顶点
	m = 10;   //10条边
    
    link(0, 3, 7);
	link(0, 5, 3);
	link(0, 2, 8);
	link(0, 1, 5);
	link(1, 2, 4);
	link(2, 3, 5);
	link(2, 5, 9);
	link(3, 5, 6);
	link(3, 4, 5);
	link(4, 5, 1);
	//下面m行都是在建图
	
	tag[0] = 1;   //从该顶点出发（把该顶点加入集合U）
	//对没有加入集合U中的顶点，都初始化closedge
	for (int i = 1; i < n; ++i) {
		closedge[i].adjvex = 0;
		closedge[i].lowcost = matrix[0][i];
	}
};

/*
Prim算法开始
*/
/
void prim() {
	int T = n - 1;
	//循环执行n-1次
	while (T--) {
		//首先寻找【不在U集合中】并且【closedge中权值最小】的边
		int mi = maxn;   //记录当前最小的权值
		int k = 0;   //最小权值时候的顶点
		for (int i = 0; i < n; ++i) {
			if (!tag[i]/*保证不在集合U中*/ && closedge[i].lowcost != -1/*保证边存在*/ && closedge[i].lowcost < mi/*保证权值最小*/) {
				mi = closedge[i].lowcost;
				k = i;
			}
		}
		cout << k << " <---> " << closedge[k].adjvex << endl;  //找到一条边
		tag[k] = 1;  //标记
		//更新closedge
		for (int i = 0; i < n; ++i) {
			if (closedge[i].lowcost == -1/*原来的边不存在*/ || (matrix[k][i] != -1 && matrix[k][i] < closedge[i].lowcost)/*保证k--i的边存在并且比原来记录的要小*/) {
				closedge[i].adjvex = k;
				closedge[i].lowcost = matrix[k][i];
			}
		}

	}
}
/

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	init();   //初始化
	prim();   //普利姆算法
	return 0;
}

4、教材P311实验题10：求有向图的简单路径

编写一个程序exp8-10.cpp，设计相关算法完成以下功能。
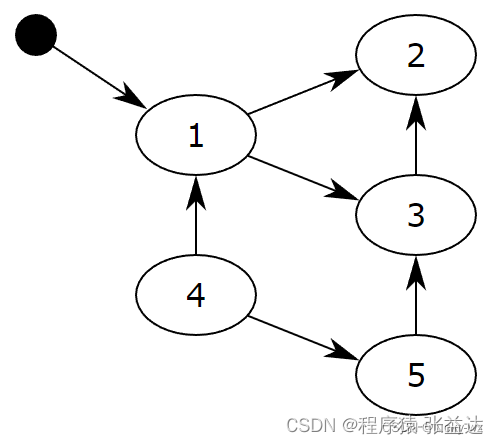
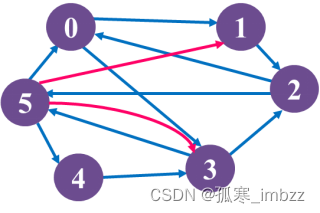
（1）输出如图8.56的有向图G从顶点5到顶点2的所有简单路径。
（2）输出如图8.56的有向图G从顶点5到顶点2的所有长度为3的简单路径。
（3）输出如图8.56的有向图G从顶点5到顶点2的最短路径。

图8.56 一个有向图

#include<iostream>
#include<queue>
using namespace std;
# define maxn 128
//邻接矩阵
int matrix[maxn][maxn];
//标记数组
int tag[maxn];
//路径数组
int path[maxn];
//边数 点数
int n, m;


void Link(int i,int j,int value=1) {
	matrix[i][j] = value;//有向的
}

/*
* 深度优先找所有路径
*/
void DFS_all_destination(int nowV,int destV,int j=0) { //起点 终点 记录的路径数组下标
	if (j == 0) {
		tag[nowV] = 1;
	}
	//当前点入路径数组
	path[j] = nowV;
	//如果到达目标 遍历输出path 返回
	if (nowV == destV) {
		for (int i = 0; i <= j; i++) {
			if (i != j) {
				cout << path[i] << "->";
			}else {
				cout << path[i]<<endl;
			}
		}
		return;
	}
	//没有到达目标 for矩阵  与该点相连的 没有被标记过的 标记
	//递归  
	//递归结束找到一条 tag清空
	for (int i = 0; i < n; i++) {
		if (!tag[i] && matrix[nowV][i] != -1) {
			tag[i] = 1;
			DFS_all_destination(i, destV, j + 1);
			tag[i] = 0;
		}
	}
}


/*
* 深度优先遍历找指定长度的所有路径
now:当前顶点
dest:目标
len:指定长度
i:当前长度
*/
void DFS_fix_dest(int nowV,int destV,int length,int j=0) {
	//标记第一个
	if (j == 0) {
		tag[nowV] == 1;
	}
	//当前节点入路径数组
	path[j] = nowV;
	//如果到达目的 长度满足 打印path 返回
	if (nowV == destV && j == length) {
		for (int i = 0; i <= j; i++) {
			if (i != j) {
				cout << path[i] << "->";
			}
			else {
				cout << path[i] << endl;
			}
		}
		return;
	}
	//如果没到达目的地并且i<length 继续 
	//i>=length,nowV!=destV 返回
	if (nowV != destV) {//还没到达
		if (j < length) {//路径小于 还有机会 递归
			for (int i = 0; i < n; i++) {
				if (!tag[i] && matrix[nowV][i] != -1) {
					tag[i] = 1;
					DFS_fix_dest(i, destV, length, j + 1);
					tag[i] = 0;
				}
			}
		}
		else {//没有机会 直接返回
			return;
		}
	}
}

/*
* 广度优先 求最短
*/
int LastV[maxn];//记录上一个顶点 方便溯源
void BFS_to_dest(int start,int end) {//开始点 结束点
	//清空数组
	for (int i = 0; i < maxn; i++) {
		tag[i] = 0;
		LastV[i] = -1;
	}
	//队列
	queue<int> que;
	//当前点入队
	que.push(start);
	// 标记
	tag[start] = 1;
	//当队列不空 出队
	int v;
	while (!que.empty()) {
		v = que.front();
		que.pop();
		if (v == end) {//如果到达结尾 跳出循环
			break;
		}
		//如果还没到达 循环 未标记且连线存在 标记 加入last数组 入队
		for (int i = 0; i < n; i++) {
			if (!tag[i] && matrix[v][i] != -1) {
				tag[i] = 1;
				LastV[i] = v;
				que.push(i);
			}
		}
	}
	int i = 0;
	while (v != -1) {//拿队尾 循环当值不是-1 记录路径
		path[i++] = v;//反向路径数组
		v = LastV[v];//溯源寻找上一个节点
	}
	
	while (--i) {
		cout << path[i] << "->";
	}
	cout <<end <<endl;
	//反向遍历输出
}

void init() {
	
	for (int i = 0; i < maxn; i++) {
		tag[i] = 0;//初始化tag数组
		for (int j = 0; j < maxn; j++) {
			matrix[i][j] = -1;//初始化 邻接矩阵
		}
	}
	//顶点数
	n = 6;

	//连接图
	Link(0, 3);
	Link(0, 1);
	Link(1, 2);
	Link(2, 0);
	Link(2, 5);
	Link(3, 2);
	Link(3, 5);
	Link(4, 3);
	Link(5, 4);
	Link(5, 0);
}

int main() {
	init();
	cout << "深度优先: 5 -> 2 所有路径:" << endl;
	DFS_all_destination(5, 2);
	cout << endl;
	memset(tag, 0, sizeof(tag));
	cout << "深度优先: 5 -> 2 长度为3所有路径:" << endl;
	DFS_fix_dest(5, 2, 3);
	cout << endl;
	memset(tag, 0, sizeof(tag));
	cout << "广度优先: 5 -> 2 最短路径:" << endl;
	BFS_to_dest(5, 2);

	return 0;
}

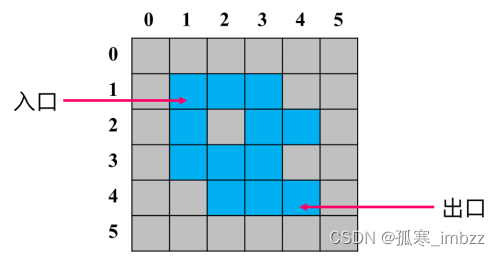
5、教材P313实验题14：用图搜索方法求解如图3.28（教材P119）的迷宫问题（也可以自建迷宫）

编写一个程序exp8-14.cpp，完成以下功能。
（1）建立一个迷宫对应的邻接表表示。
（2）采用深度优先遍历算法输出从入口（1，1）到出口（M,N）的所有迷宫路径。

图3.28 迷宫示意图

#include<iostream>
#include<vector>
using namespace std;

//标记数组
int tag[6][6] = { 0 };

//迷宫
vector<vector<int>> m{
	{0,0,0,0,0,0},
	{0,1,1,1,0,0},
	{0,1,0,1,1,0},
	{0,1,1,1,0,0},
	{0,0,1,1,1,0},
	{0,0,0,0,0,0}
};

struct Proint;
struct vNode;
//顶点
struct Point {
	int x;
	int y;
	vNode* firstNode;
	Point(int i, int j) {
		this->x = i;
		this->y = j;
		this->firstNode = 0;
	}
}*Plist[6][6];

//邻接表节点
struct vNode {
	Point* p;//顶点的邻点
	vNode* next;//构建链表
};



//初始化函数
void init(vector<vector<int>>arr, int xlen, int ylen) {
	//初始化顶点矩阵
	for (int i = 0; i < xlen; i++) {
		for (int j = 0; j < ylen; j++) {
			if (arr[i][j]) {//如果有就赋值
				Plist[i][j] = new Point(i,j);
			}
			else {
				Plist[i][j] = 0;
			}
		}
	}

	//
	int four[2][4] = { {0,0,1,-1} ,{1,-1,0,0} };
	int x, y;
	//初始化邻接表
	for (int i = 0; i < xlen; i++) {
		for (int j = 0; j < ylen; j++) {
			if (arr[i][j]) {//当前有值 判断四周
				for (int k = 0; k < 4; k++) {
					x = i + four[0][k];
					y = j + four[1][k];
					if (x >= 0 && x <= xlen && y >= 0 && y <= ylen&&m[x][y]!=0) {//在矩阵范围内
						vNode* closeNode = new vNode();//邻节点
						closeNode->p = Plist[x][y];//连接邻近 point
						closeNode->next = Plist[i][j]->firstNode;//接入邻接表
						Plist[i][j]->firstNode = closeNode;
					}
				}
			}
		}
	}

}

/*
* 深度优先搜索
*/
Point*path[36]; //顶点指针 内含坐标
void DFS(int x, int y, int endx, int endy, int i = 0) {
	//记录路径
	if (i == 0) {
		tag[x][y] = 1;
	}
	path[i] = Plist[x][y];
	//如果到达终点 打印数组 返回
	if (x == endx && y == endy) {
		for (int j = 0; j <=i; j++) {
			if (j != i) {
				cout << "(" << path[j]->x << "," << path[j]->y << ")->";
			}
			else {
				cout << "(" << path[j]->x << "," << path[j]->y <<")" << endl;
			}
		}
		return;
	}
	//没有达到终点 
	vNode* temp = Plist[x][y]->firstNode;
	//遍历邻接表 没有标记 就标记 递归 去掉标记
	int mx, my;
	while (temp) {
		mx = temp->p->x;
		my = temp->p->y;
		if (!tag[mx][my]) {
			tag[mx][my] = 1;
			DFS(mx, my, endx, endy, i + 1);
			tag[mx][my] = 0;
		}
		temp = temp->next;
	}
}

int main() {
	init(m, m[0].size(), m.size());//赋初值0
	DFS(1, 1, 4, 4);//深度优先查找
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/190208.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Springboot扩展点之BeanFactoryPostProcessor

Springboot扩展点之BeanFactoryPostProcessor

Springboot扩展点之BeanFactoryPostProcessor1.功能特性BeanFactoryPostProcessor的执行是Spring Bean生命周期非常重要的一部分&#xff1b; BeanFactory级别的后置处理器&#xff0c;在Spring生命周期内&#xff0c;org.springframework.beans.factory.config.BeanFactoryPos…
阅读更多...
【C语言】10题相关讲解+总结----有用的知识1

【C语言】10题相关讲解+总结----有用的知识1

总结【C语言】10题&#xff0c;有兴趣的可以看看1.结构体与typedef联系2.结构体中涉及的操作符3.指针数组与数组指针4.数组首元素的作用5.喝汽水问题6.上三角矩阵判定7 矩阵相等判定8.VS调试技巧9.Debug与Release关系10.调整奇数偶数顺序11.有序序列合并1.结构体与typedef联系 …
阅读更多...
开发互动直播应用很简单：声网 Android Demo保姆级运行教程

开发互动直播应用很简单：声网 Android Demo保姆级运行教程

本文作者是来自声网开发者社区的用户“Xiaohua”。 前言 本人在参与《声网开发者漫游指南》期间&#xff0c;通过学习了解和学会跑通声网的实时互动Demo&#xff0c;但因为课程提供的demo是移动端和pc端的&#xff0c;很少接触过&#xff0c;所以只能花点时间学习一下才能运行…
阅读更多...
如何屏蔽 iOS 软件自动更新，去除更新通知和标记

如何屏蔽 iOS 软件自动更新，去除更新通知和标记

如何禁用 iPhone、iPad 软件自动更新。适用于 iOS、iPadOS 和 watchOS&#xff0c;即 iPhone、iPad 和 Apple Watch 通用。 请访问原文链接&#xff1a;https://sysin.org/blog/disable-ios-update/&#xff0c;查看最新版。原创作品&#xff0c;转载请保留出处。 作者主页&a…
阅读更多...
WebAssembly编译之(4)-WASM编译进阶(多文件、多接口)

WebAssembly编译之(4)-WASM编译进阶(多文件、多接口)

引言 上一节我们讲到如何用Emscripten将一个C编译陈wasm&#xff0c;并导出可供Javascirpt调用的接口&#xff0c;以及C导出类的函数接口、导出类的封装对象等。然而&#xff0c;编译的方式比较玛法&#xff0c;有没办法能更友好一点实现wasm的编译呢 WASM 相关文档&#xff1a…
阅读更多...
【自学Docker】Docker diff命令

【自学Docker】Docker diff命令

Docker diff命令 大纲 docker diff命令教程 docker diff 命令用于比较一个 Docker容器 不同版本提交的文件差异。该命令后面的 CONTAINER 可以是容器Id&#xff0c;或者是容器名。 docker diff命令会列出 3 种容器内文件状态变化&#xff08;A - Add, D - Delete, C - Chang…
阅读更多...
Java-基础-3.容器

Java-基础-3.容器

一&#xff1a;为什么会出现容器&#xff1f; 在之前的学习中&#xff0c;我们学习了变量和常量。都是一个字符或者字符串&#xff0c;数字的情况。但是在实际的生产中&#xff0c;我们一次会接受到很多类型不同&#xff0c;个数不同的数据。所以&#xff0c;为了方便我们后续…
阅读更多...
红杉：2022企业数字化年度指南

红杉：2022企业数字化年度指南

省时查报告-专业、及时、全面的行研报告库省时查方案-专业、及时、全面的营销策划方案库【免费下载】2022年12月份热门报告盘点罗振宇2023年跨年演讲PPT原稿吴晓波2022年年终秀演讲PPT原稿2023年&#xff0c;如何科学制定年度规划&#xff1f;《底层逻辑》高清配图华为2021数字…
阅读更多...
[基础语法] python语法之列表的基本操作

[基础语法] python语法之列表的基本操作

文章目录列表已发布列表的基本操作增删改查排序列表实例练习列表 已发布 python判断语句python循环语句python之列表list python 的数据格式主要有列表、字典、元组、集合。其中列表的使用最为广泛。 任何一种数据格式的使用都离不开增、删、改、查四个操作。列表除了这四个…
阅读更多...
【Mysql第四期 运算符规则计算】

【Mysql第四期 运算符规则计算】

文章目录写在前面1.算数运算符2.比较运算符3.逻辑运算符4.位运算符5.运算符的优先级拓展&#xff1a;使用正则表达式查询写在前面 基本的运算符号在计算机编程领域都是相通的&#xff0c;会有自己的一些特定符号语言&#xff0c;就像是各地的普通话一样&#xff0c;尽管语音描…
阅读更多...
剑指 Offer II 004只出现一次的数字

剑指 Offer II 004只出现一次的数字

给你一个整数数组 nums &#xff0c;除某个元素仅出现 一次 外&#xff0c;其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。 示例 1&#xff1a; 输入&#xff1a;nums [2,2,3,2] 输出&#xff1a;3 示例 2&#xff1a; 输入&#xff1a;nums [0,1,0,…
阅读更多...
Linux中Vi编辑器和Vim编辑器

Linux中Vi编辑器和Vim编辑器

✅作者简介&#xff1a;热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏&#xff1a;Java案例分…
阅读更多...
Docker常用命令总结

Docker常用命令总结

基础命令 1.启动docker systemctl start docker 2.关闭docker systemctl stop docker 3.设置docker为自启动 systemctl enable --now docker 4.重启docker systemctl restart docker 3.查看docker版本信息 docker version 4.查看docker详细信息 docker info Clien…
阅读更多...
Spring定时器超过30分钟问题

Spring定时器超过30分钟问题

目前需要定时器做一个定时扫描任务的功能&#xff0c;原先都是定时在半个小时&#xff0c;程序跑起来也没事。但是最近公司要求定时时间加长到45分钟&#xff0c;而调整完配置完后发现&#xff0c;程序是在45分钟和整点进行的扫描。 下面是我做的示例时间缩短为45秒 spring。x…
阅读更多...
守护进程编程流程及代码实现

守护进程编程流程及代码实现

概念不做阐述&#xff0c;本文主要内容为守护进程编程部分的知识说明 守护进程的编程流程&#xff1a; 1.fork退出父进程&#xff0c;保证留下的子进程是组员进程 2.利用setsid()创建新会话&#xff0c;把子进程挪到新的会话中 //获取会话是getsid() 3.fork退出父进程&#x…
阅读更多...
完成基于Servlet的对user表的增删改查

完成基于Servlet的对user表的增删改查

基于Servlet的增删改查 1.开发环境 IDEAJDK1.8Tomcat8.5Mysql 8.0.12 2.数据库 2.1表创建 2.2表数据 3.JavaWeb代码 3.1目录结构 3.2util包下代码 JdbcUtil完成对数据库的连接和资源释放 JsonResult对返回前端资源的封装 JdbcUtil代码&#xff1a; /* 数据库连接板帮助类 …
阅读更多...
Python中的垃圾回收机制

Python中的垃圾回收机制

Python的垃圾回收主要以引用计数为主&#xff0c;分代回收为辅。引用计数在Python中&#xff0c;使用了引用计数这一技术实现内存管理。一个对象被创建完成后就有一个变量指向这个对象&#xff0c;那么就这个对象的引用计数为1&#xff0c;以后如果有其他变量指向这个对象&…
阅读更多...
不吹牛，完爆ant design的定位组件，floating-ui来也

不吹牛，完爆ant design的定位组件，floating-ui来也

前言 因为要写react定位组件&#xff08;这不是标题党&#xff0c;就是完爆ant design的定位组件&#xff0c;你应该看到一半就会同意我的观点&#xff09;&#xff0c;如下图&#xff1a; 红框部分是用绝对定位放在按钮上面的&#xff0c;你们B端用的主流组件库都是这样实现的…
阅读更多...
Python自动化小技巧14——自动批量发送邮件（带各种附件）

Python自动化小技巧14——自动批量发送邮件（带各种附件）

案例背景 我的博客下面评论都是各种要数据的......一个一个发其实很浪费时间的&#xff0c;每次输入评论者的邮箱&#xff0c;然后打开数据所在的文件夹&#xff0c;上传&#xff0c;填写标题正文&#xff0c;发送....... 一模一样的流程&#xff0c;所以这种重复性的劳动肯定…
阅读更多...
Linux下 git 上传与删除 的基本指令

Linux下 git 上传与删除 的基本指令

git的概述克隆仓库使用 git 上传文件删除 git 中的文件git的概述 Git 是一个免费并开源的分布式版本控制系统&#xff0c;可以快速高效地处理从小型到大型的各种项目。 在使用 git 应确保Linux系统中已安装有git 命令&#xff1a;git --version 作用&#xff1a;查看 git 是否…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023