剑指 Offer II 004只出现一次的数字

news2024/9/20 9:43:02

给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现三次。请你找出并返回那个只出现了一次的元素。

示例 1：

输入：nums = [2,2,3,2]
输出：3
示例 2：

输入：nums = [0,1,0,1,0,1,100]
输出：100

提示：

1 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
nums 中，除某个元素仅出现一次外，其余每个元素都恰出现三次

进阶：你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

知识点：

1.哈希表

1.1 getOrDefault（）方法，初始化元素

1.2哈希表的特点，一个key对应一个value

2.DFA算法

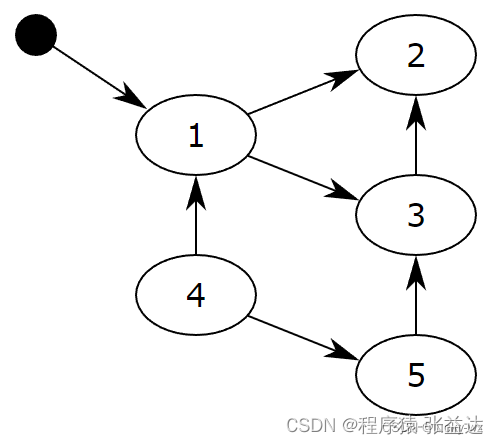
DFA，全称 Deterministic Finite Automaton 即确定有穷自动机：从一个状态通过一系列的事件转换到另一个状态，即 state -> event -> state。

确定：状态以及引起状态转换的事件都是可确定的，不存在“意外”。
有穷：状态以及事件的数量都是可穷举的。

如下图所示，其中椭圆表示状态，状态之间的连线表示事件，进程的状态以及事件都是可确定的，且都可以穷举。

DFA示例1

（普通版）方法一：哈希表

因为思路是同一个数字出现多少次很明显是一个数字对应这它的次数，这个时候我们就可以想到哈希表的特征。因而最终挑选出值为1的key即可

class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer,Integer> map = new HashMap<Integer,Integer>();
        for(int num : nums){
            //getOrDefault初始化key的value为0
            map.put(num,map.getOrDefault(num,0)+1);
        }
        for(int num : map.keySet()){
            if(map.get(num)==1) return num;
        }
        return -1;
    }
}

方法二：进阶：位运算、位数统计（巧妙）

因为是整数int，所以最多有32个比特位。所以创建一个32位的数组模拟出一个二进制位，思路就是每一个数字都可以转化为二进制数，然后都加到数组里，最终的结果模上3（%3），相当于我们把出现三次的数字给去除掉了（这个位置好好品、好好琢磨）。

求每个数字的二进制位：对于数组的元素num,使用(x >> i) & 1得到x的第i个二进制位，并将他们相加对3取余，得到的结果一定为0或1，即答案的第i个二进制位

例子：[1,1,1,3]，1和3的二进制位分别是01和11，相加后得0.0.0......0.1.4。然后%3得0.0.0......0.1.1 再转化为十进制就是3

lass Solution {
    public int singleNumber(int[] nums) {
        int[] count = new int[32];
        //将数字的每个一二进制位存入对应位置
        for (int num : nums) {
            for (int i = 0; i < 32; i++) {
                if (((num >> i) & 1) == 1) {
                    count[i]++;
                }
            }
        }
        int ans = 0;
        //计算出数字
        for (int i = 0; i < 32; i++) {
            if ((cnt[i] % 3 & 1) == 1) {
                ans += (1 << i);
            }
        }
        return ans;
    }
}