星期一:
补cf global round26 D cf传送门

思路:把s中非a字符存下来,共m个,然后暴力检测,复杂度有点迷
代码如下:
ll n;
void solve(){
string s; cin >> s;
n=s.size(); s=" "+s;
if(count(s.begin(),s.end(),'a')==n){cout << n-1 << "\n"; return ;}
vector<int>ve;
int m=0;
for(int i=1;i<=n;i++)
if(s[i]!='a') ve.push_back(i),m++;
ll ans=0;
for(int i=1;i<=m;i++){ //枚举t的长度
if(m%i) continue;
bool if1=1;
int r=n-ve[m-1],mi=1e9;
for(int j=0;j<m;j++){
if(j<m-i && s[ve[j]]!=s[ve[j+i]]){if1=0; break;}
if(j<m-i-1 && (j+1)%i && ve[j+1]-ve[j]!=ve[j+i+1]-ve[j+i]){if1=0; break;}
if((j+1)%i==0 && j!=m-1) mi=min(ve[j+1]-ve[j]-1,mi);
}
if(!if1) continue;
for(int j=0;j<ve[0] && j<=mi;j++) ans+=min(r+1,mi-j+1);
}
cout << ans << "\n";
}星期二:
补cf round954 div3 D cf传送门

题意:给一串长度为n的数,在里面填 n-2个+或*号,使结果最小
思路:这里我本来想的贪心选一个二位数,但wa,其实可以枚举二位数的选择,这种情况下就没必要贪心了,直接枚举肯定比贪心更稳健
代码如下:
ll n;
string s;
void solve(){
cin >> n >> s;
if(n==2){
if(s[0]=='0') cout << s[1] << "\n";
else cout << s << "\n";
return ;
}
if(n==3){
if(s[0]=='0' || s[2]=='0'){cout << "0\n"; return ;}
ll ans=0;
int a1=s[0]-'0',a2=(s[1]-'0')*10+s[2]-'0';
ans=min(a1+a2,a1*a2);
a1=(s[0]-'0')*10+s[1]-'0',a2=s[2]-'0';
ans=min({1ll*a1+a2,1ll*a1*a2,ans});
cout << ans << "\n";
return ;
}
ll tot=0,ans=1e9;
for(auto i:s){
if(i!='1') tot+=i-'0';
if(i=='0'){cout << "0\n"; return ;}
}
s=" "+s;
for(int i=1;i<n;i++){
int num=(s[i]-'0')*10+s[i+1]-'0',ms=0; //枚举
if(s[i]!='1') ms+=s[i]-'0';
if(s[i+1]!='1') ms+=s[i+1]-'0';
ans=min(num+tot-ms,ans);
}
cout << ans << "\n";
}星期三:
补cf round 955 div2 C 拿牌 cf传送门

思路:dp【i】表示拿到第 i张牌能赢的最大轮数
前缀和处理,对每个点,先和dp【i-1】取max,二分找出下一次赢的轮的拿牌范围,即 i+1到 idx,dp【idx】和 dp【i】+1 取max
代码如下:
const int N=2e6+10;
ll n;
ll a[N],dp[N];
void solve(){
ll l,r; cin >> n >> l >> r;
for(int i=1;i<=n;i++){
cin >> a[i];
a[i]+=a[i-1];
dp[i]=0;
}
ll ans=0;
for(int i=0;i<=n;i++){
if(i) dp[i]=max(dp[i-1],dp[i]);
int idx=lower_bound(a+1+i,a+1+n,a[i]+l)-a;
if(a[idx]-a[i]>r) continue;
if(idx>n){cout << ans << "\n"; return ;}
dp[idx]=max(dp[i]+1,dp[idx]);
ans=max({dp[i],dp[idx],ans}); //记录出现过的最大值
}
cout << ans << "\n";
}补cf round954 div3 E cf传送门

题意:给一数组,可以任意排序,有一操作为使其一元素+=k,问最少操作次数使其对称,不可能则输出 -1
思路:显然俩相同的数可以直接忽略,所以只考虑奇数个的数
俩数可以通过操作相等即俩数对 k的模数相等,所以按模数分类,n为奇则允许有一类是奇数个数
如果是偶数个,排序后直接对相邻数操作即可,奇数个需要枚举忽略哪个数,比较繁琐
代码如下:
const int N=2e6+10;
ll n;
ll a[N];
void solve(){
ll k; cin >> n >> k;
map<int,int>b;
for(int i=1;i<=n;i++){
cin >> a[i];
b[a[i]]++;
}
map<int,vector<int>>mp;
for(auto [x,y]:b) if(y&1) mp[x%k].push_back(x);
bool if1=n&1;
ll ans=0;
for(auto [x,ve]:mp){
if(ve.size()&1){
if(!if1){cout << "-1\n"; return ;}
if1=0;
if(ve.size()==1) continue;
}
sort(ve.begin(),ve.end());
ll tmp=0;
if(ve.size()&1){
vector<ll>ve1,ve2;
ve1.push_back(0),ve2.push_back(0);
for(int i=1,sz=ve.size();i<sz;i++){
if(i&1){
ve1.push_back(ve1.back()+(ve[i]-ve[i-1])/k);
ve2.push_back(ve2.back());
}else{
ve2.push_back(ve2.back()+(ve[i]-ve[i-1])/k);
ve1.push_back(ve1.back());
}
}
tmp=1e18;
for(int i=0,sz=ve.size();i<sz;i++){
if(i&1){
if(i>1) tmp=min((ve[i+1]-ve[i-1])/k+ve1[i-2]+ve2.back()-ve2[i+1],tmp);
else tmp=min((ve[i+1]-ve[i-1])/k+ve1[i-2]+ve2.back()-ve2[i+1],tmp);
}else{
if(i) tmp=min(ve1[i-1]+ve2.back()-ve2[i],tmp);
else tmp=min(ve2.back(),tmp);
}
}
}else for(int i=0,sz=ve.size();i<sz;i+=2) tmp+=(ve[i+1]-ve[i])/k;
ans+=tmp;
}
cout << ans << "\n";
}星期四:
24百度之星 括号 mtj传送门
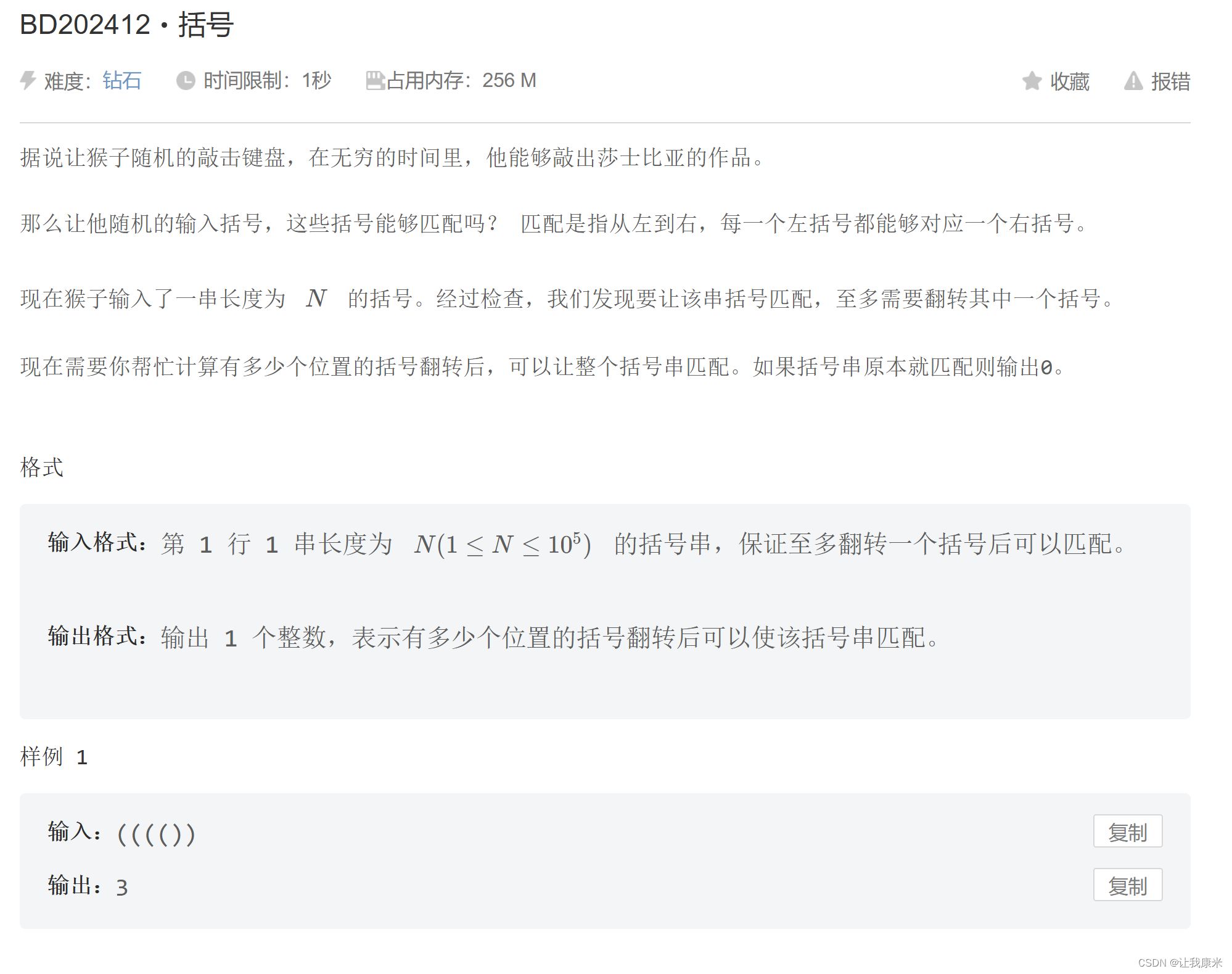
思路:先看左右括号差值是否为2,
代码如下:
ll n;
void solve(){
string s; cin >> s;
int cntl=0,cntr=0;
for(auto i:s) cntl+=i=='(',cntr+=i==')';
if(abs(cntl-cntr)!=2){cout << 0; return ;}
n=s.size();
s=" "+s;
ll ans=0;
stack<int>sk;
if(cntl>cntr){
for(int i=n;i;i--){
if(s[i]==')') sk.push(i);
else{
if(sk.size()>=0) ans++;
if(sk.empty()) break;
else sk.pop();
}
}
}else{
for(int i=1;i<=n;i++){
if(s[i]=='(') sk.push(i);
else{
if(sk.size()>=0) ans++;
if(sk.empty()) break;
else sk.pop();
}
}
}
cout << ans;
}学了下汉诺塔问题,一知半解
ll n;
void move(int n,char a,char b,char c){
if(!n) return ;
move(n-1,a,c,b);
cout << a << " -> " << c << "\n";
move(n-1,b,a,c);
}
void solve(){
cin >> n;
char a='A',b='B',c='C';
move(n,a,b,c);
}星期五:
补cf edu round 167 D cf传送门

题意有点怪,看了两遍才懂
可以贪心,但我用multiset装金属块T了后,看了jly的dp写法,感觉很不错
思路:f【i】表示用 i块造一次可达到的最小损失,dp【i】表示用 i块开造最多能造多少次
首先使 f【i】单调不递增,因为数量越多,选择就越多,损失数只可能更少,然后dp可以线性转移
代码如下:
const int N=2e6+10;
ll n;
int a[N],f[N];
ll dp[N];
void solve(){
int m; cin >> n >> m;
int ma=0;
for(int i=1;i<=n;i++){
cin >> a[i];
ma=max(a[i],ma);
}
for(int i=1;i<=ma;i++) f[i]=1e9;
for(int i=1;i<=n;i++){
int b; cin >> b;
f[a[i]]=min(a[i]-b,f[a[i]]);
}
for(int i=2;i<=ma;i++) f[i]=min(f[i-1],f[i]);
for(int i=1;i<=ma;i++) if(f[i]<=i) dp[i]=dp[i-f[i]]+1;
ll ans=0;
while(m--){
int c; cin >> c;
if(c>ma){ //数量大于最大,就先处理到最大
int ti=(c-ma)/f[ma]; if((c-ma)%f[ma]) ti++;
c-=f[ma]*ti;
ans+=ti;
}
ans+=dp[c];
}
cout << ans*2;
}牛客小白月赛97 C 牛客传送门
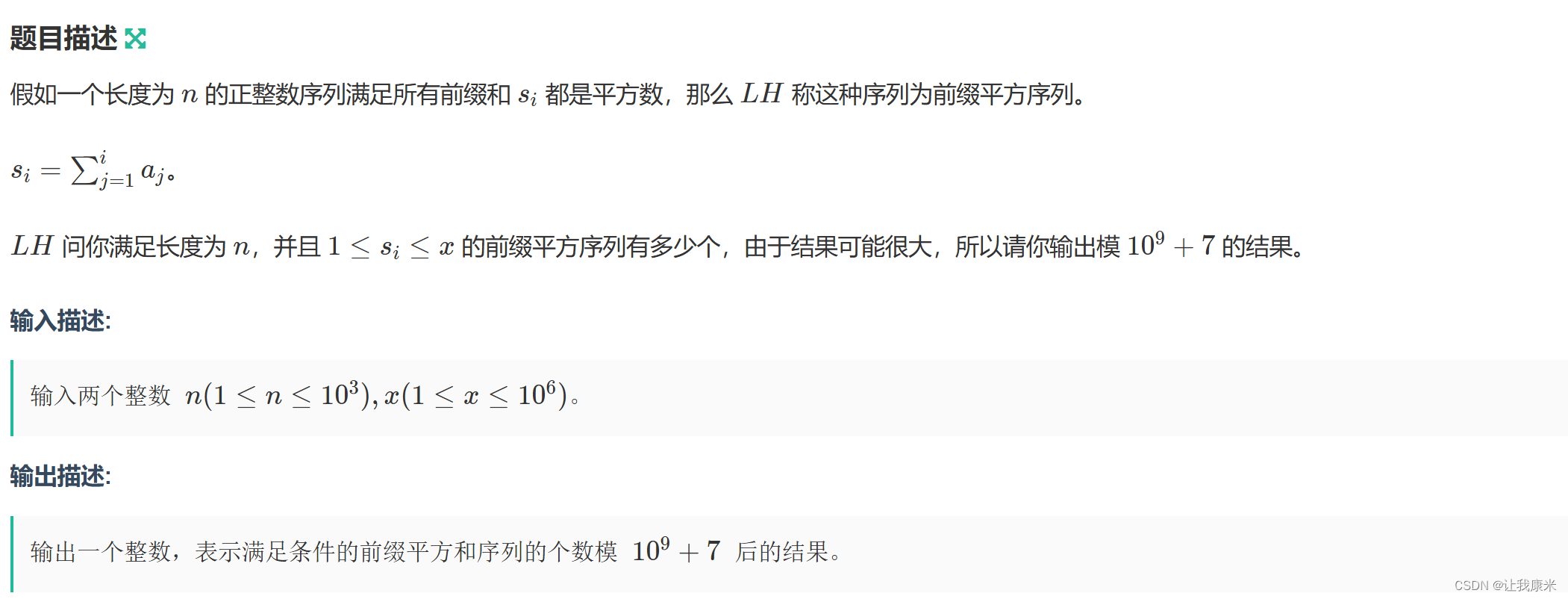
思路:翻译下就是,有 num个不同的数,单调递增地连续放置 n个的方案数
暴力转移 n^3,可以用前缀和优化到 n^2
因为最后 ans忘记取模了,白wa一发,所以记录下
代码如下:
ll n;
ll x;
ll dp[1010][1010];
void solve(){
cin >> n >> x;
vector<int>ve;
ve.push_back(0);
ll num=0;
for(int i=1;i<=x;i++){
if(i*i<=x) ve.push_back(i),num++;
else break;
}
for(int i=1;i<=num;i++) dp[1][i]=1;
for(int i=2;i<=n;i++){
for(int j=i;j<=num;j++)
dp[i][j]+=dp[i-1][j-1];
for(int j=i+1;j<=num;j++) dp[i][j]+=dp[i][j-1],dp[i][j]%=mod;
}
ll ans=0;
for(int i=n;i<=num;i++) ans+=dp[n][i],ans%=mod;
cout << ans;
}24百度之星 小度的01串 mtj传送门

思路:手操一下能发现合并的规律,和前一段长度的奇偶性有关
其余部分都很常规,第一发update里的懒标记没写为^=1,wa了一发
代码如下:
ll n;
string s;
struct seg_Tree{
#define lc p<<1
#define rc p<<1|1
struct nod{
int l,r;
int op1,op0; //改为10串的和改为01串的操作次数
int tag;
}t[N<<2];
int ql,qr;
nod merge(nod a,nod b){
nod res;
res.l=a.l,res.r=b.r;
if((a.r-a.l+1)&1){
res.op1=a.op1+b.op0;
res.op0=a.op0+b.op1;
}else{
res.op1=a.op1+b.op1;
res.op0=a.op0+b.op0;
}
return res;
}
void pushup(int p){t[p]=merge(t[lc],t[rc]);}
void pushdn(int p){
if(!t[p].tag) return ;
swap(t[lc].op1,t[lc].op0);
swap(t[rc].op1,t[rc].op0);
t[lc].tag^=t[p].tag;
t[rc].tag^=t[p].tag;
t[p].tag=0;
}
void bd(int p,int l,int r){
t[p]={l,r,0,0,0};
if(l==r){
t[p].op0=s[l]=='1';
t[p].op1=s[l]=='0';
return ;
}
int mid=l+r>>1;
bd(lc,l,mid);
bd(rc,mid+1,r);
pushup(p);
}
void update(int p){
if(ql<=t[p].l && qr>=t[p].r){
swap(t[p].op1,t[p].op0);
t[p].tag^=1;
return ;
}
int mid=t[p].l+t[p].r>>1;
pushdn(p);
if(ql<=mid) update(lc);
if(qr>mid) update(rc);
pushup(p);
}
nod query(int p){
if(ql<=t[p].l && qr>=t[p].r) return t[p];
int mid=t[p].l+t[p].r>>1;
pushdn(p);
if(ql>mid) return query(rc);
if(qr<=mid) return query(lc);
return merge(query(lc),query(rc));
}
void updt(int l,int r){
ql=l,qr=r;
update(1);
}
int ask(int l,int r){
ql=l,qr=r;
nod ans=query(1);
return min(ans.op0,ans.op1);
}
}tr;
void solve(){
int q; cin >> n >> q;
cin >> s; s=" "+s;
tr.bd(1,1,n);
while(q--){
int op,l,r; cin >> op >> l >> r;
if(op==1) tr.updt(l,r);
else cout << tr.ask(l,r) << "\n";
}
}星期六:
补牛客小白月赛97 D 牛客传送门
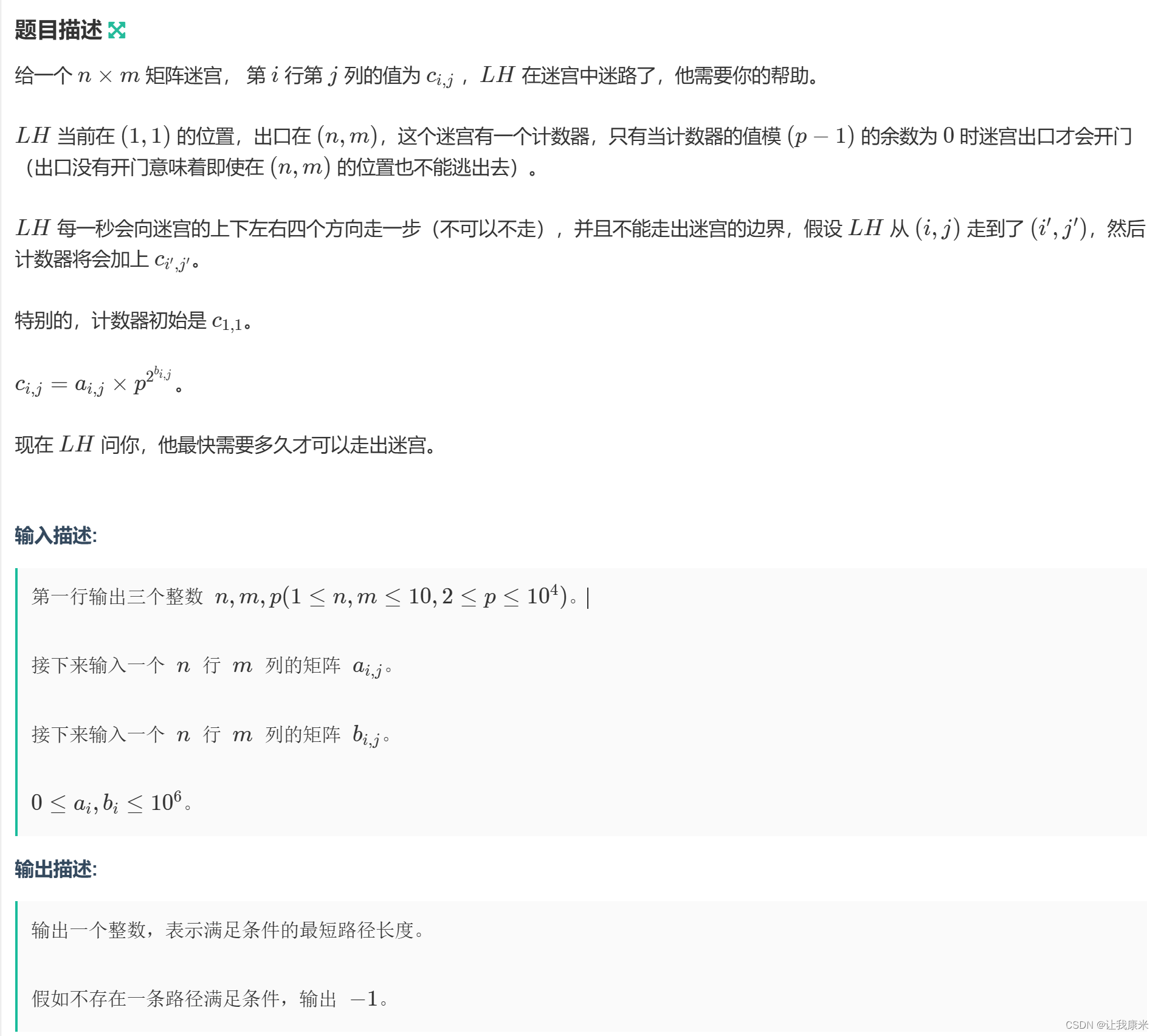
被c的计算式子诈骗了,其实p的任意次幂%(p-1)的结果都是1,所以c其实就等于a
思路:注意到n和m在10以内,p不大,对(p-1)的模数也在1e4以内,可以直接暴力bfs,vi数组标记出现过的状态(即坐标和对(p-1)的模数,出现符合条件状态就结束,bfs完毕就输出-1
还有一个特判需要注意,如果一开始就符合条件,输出0(wa了一发
代码如下:
ll n;
int dx[]={-1,1,0,0};
int dy[]={0,0,-1,1};
int a[11][11];
bool vi[11][11][10004];
struct nod{
int x,y;
ll sum,ti;
};
void solve(){
int m,p; cin >> n >> m >> p;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
cin >> a[i][j];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
int b; cin >> b;
}
if(n==1 && m==1 && p==2){cout << 0; return ;}
queue<nod>qu;
qu.push({1,1,a[1][1]%(p-1),0});
vi[1][1][a[1][1]%(p-1)]=1;
while(!qu.empty()){
nod t=qu.front(); qu.pop();
for(int i=0;i<4;i++){
int x=t.x+dx[i],y=t.y+dy[i];
ll sum=(t.sum+a[x][y])%(p-1);
if(x<1 || x>n || y<1 || y>m || vi[x][y][sum]) continue;
if(!sum && x==n && y==m){cout << t.ti+1; return ;}
qu.push({x,y,sum,t.ti+1});
vi[x][y][sum]=1;
}
}
cout << -1;
}在蓝桥杯上打了个不知道什么比赛,随便贴个线段树题 传送门

学了线段树的后果就是老想着用线段树
思路:线段树暴力维护,因为身高最高到1e9,所以动态开点,找领操用二分,操作都很常规
又因为 fnd的 k没开ll,wa了一发。
代码如下:
const int N=3e5+10,M=210;
ll n;
const int MAXN=1e9+10;
struct d_Seg_Tree{
#define lc(x) t[x].ch[0]
#define rc(x) t[x].ch[1]
struct nod{
int ch[2]; //左右儿子节点的编号
ll sum;
}t[N*55];
int root;
ll tot;
int ql,qr,qv;
void pushup(int p){
t[p].sum=t[lc(p)].sum+t[rc(p)].sum;
}
void update(int &p,int l,int r){
if(!p) p=++tot; //新建节点
if(ql<=l && qr>=r){
t[p].sum+=qv;
return ;
}
int mid=l+r>>1;
if(ql<=mid) update(lc(p),l,mid);
if(qr>mid) update(rc(p),mid+1,r);
pushup(p);
}
void updt(int l,int r,int v){
ql=l,qr=r;
qv=v;
update(root,1,MAXN);
}
int fnd(int &p,int l,int r,ll k){
if(!p) return 0;
if(l==r) return l;
int mid=l+r>>1;
if(t[lc(p)].sum>=k) return fnd(lc(p),l,mid,k);
else return fnd(rc(p),mid+1,r,k-t[lc(p)].sum);
}
}tr;
void solve(){
cin >> n;
ll num=0;
for(int i=1;i<=n;i++){
int v,a; cin >> v >> a;
num+=a;
tr.updt(v,v,a);
ll ld=num/2; if(num&1) ld++;
cout << tr.fnd(tr.root,1,MAXN,ld) << "\n";
}
}周日:
23年百度之星 dp mtj传送门
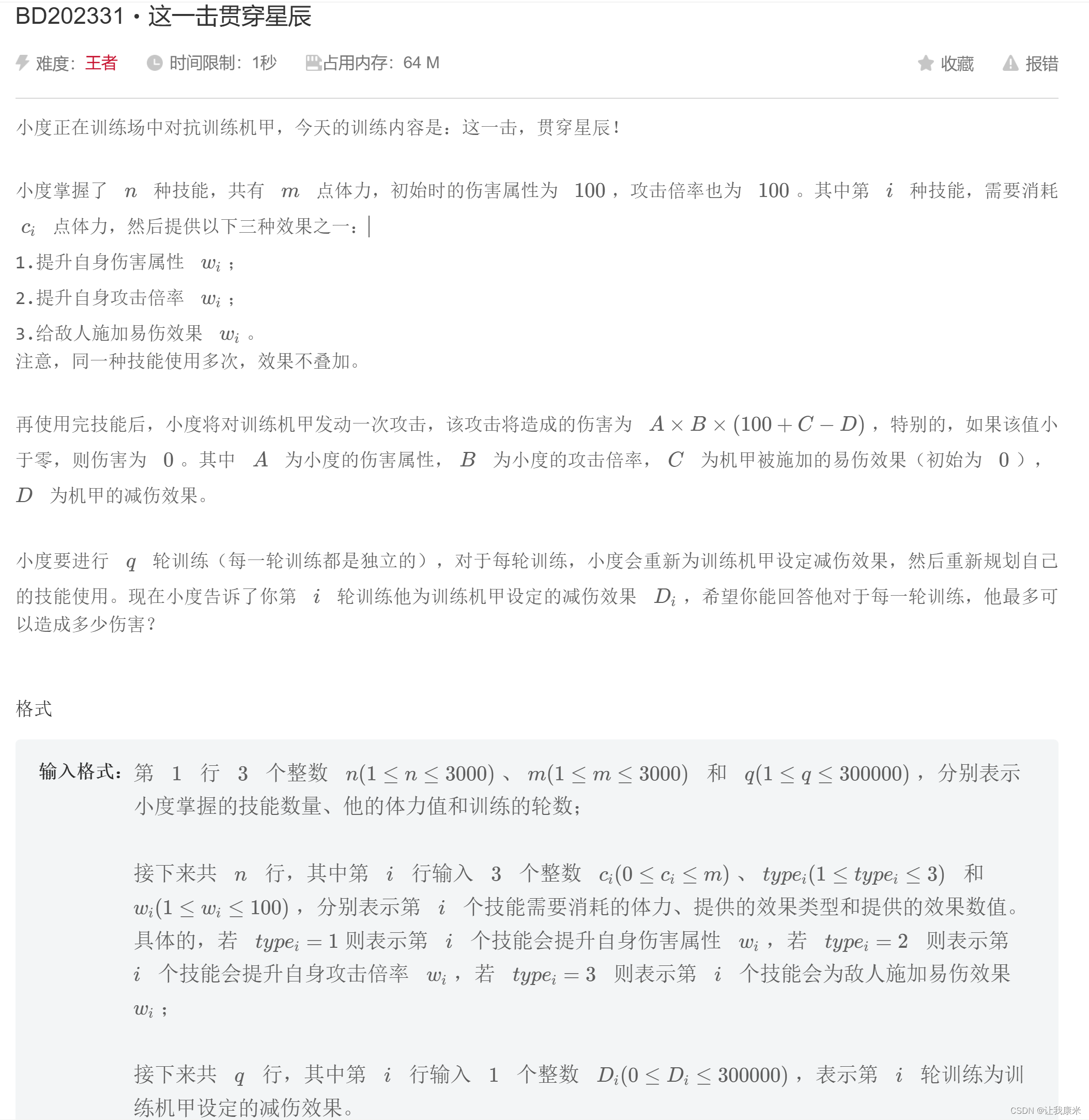
dp【i】表示消耗 i蓝最大的A*B值,dpc【i】表示消耗 i蓝最大的100+C值
思路:题意有点复杂,看似伤害和ABCD的值都相关,要考虑四个,实际上经过处理后只需考虑两个值,即A*B和C-d(C为原题意的100+C,这样就能线性即3e3地处理询问,但复杂度仍是9e8,对于1s来说是不够的
然而只需加上一个vi数组来记录出现过的答案,只消这么一个优化,就能从T 2~5个点变为200ms跑完,这让我明白在复杂度很危险的情况下,任何能想到的优化都是有必要的
代码如下:
const int N=3e5+10;
ll n;
vector<PII>ve[4];
ll dpa[3030],dpb[3030],dp[3030];
ll dpc[3030];
ll vi[N];
void solve(){
int m,q; cin >> n >> m >> q;
for(int i=0;i<=m;i++) dpa[i]=dpb[i]=dpc[i]=100;
for(int i=1;i<=n;i++){
int c,tp,w; cin >> c >> tp >> w;
ve[tp].push_back({c,w});
}
for(auto [c,w]:ve[1]){ //A
for(int j=m;j>=c;j--)
dpa[j]=max(dpa[j-c]+w,dpa[j]);
}
for(auto [c,w]:ve[2]){ //B
for(int j=m;j>=c;j--)
dpb[j]=max(dpb[j-c]+w,dpb[j]);
}
for(int i=0;i<=m;i++){
for(int j=0;j<=i;j++){ //A * B
int k=i-j;
dp[i]=max(dpa[j]*dpb[k],dp[i]);
}
}
for(auto [c,w]:ve[3]){ //C
for(int j=m;j>=c;j--)
dpc[j]=max(dpc[j-c]+w,dpc[j]);
}
memset(vi,-1,sizeof vi);
while(q--){
int d; cin >> d;
if(vi[d]!=-1){cout << vi[d] << "\n"; continue;}
if(dpc[m]+100<=d){cout << "0\n",vi[d]=0; continue;}
ll ans=0;
for(int i=0;i<=m;i++){
int j=m-i;
ans=max(dp[i]*(dpc[j]-d),ans);
}
cout << ans << "\n";
vi[d]=ans;
}
}百度之星第三场:那道字符串哈希,毁了我的国赛梦





![[单master节点k8s部署]20.监控系统构建(五)Alertmanager](https://img-blog.csdnimg.cn/direct/1677f991002140ab82ff06465a97f27f.png)