智能优化算法的基准测试函数是用于评估和优化算法性能的一组标准问题。这些测试函数模拟了真实世界优化问题的不同方面,包括局部最小值、全局最优解、高维度、非线性、不连续等复杂性。以下是对智能优化算法基准测试函数的详细归纳:
- 测试函数的分类:
- 单模函数:如Sphere、Rosenbrock和Quartic函数,它们只有一个全局最优解,适合测试算法的收敛速度和精确性。
- 多模函数:例如Rastrigin、Griewank和Ackley函数,具有多个局部最优解和一个全局最优解,用于检验算法是否能够避免局部最小陷阱并找到全局最优。
- 组合函数:如Schwefel函数和Fletcher-Powell函数,结合了多种问题特点,提供了更复杂的优化挑战。
- 约束优化问题:含有一系列约束条件的优化问题,要求算法在寻优时遵守这些约束条件。
- 具体测试函数举例:
- Sphere函数:定义为f(x) = ∑i=1Dxi2,其中D是变量维度,该函数是优化算法中最基本的测试函数之一。
- Rosenbrock函数:具有狭长的抛物形状谷,用于测试算法在平坦区域的搜索能力。
- Rastrigin函数:具有许多局部最小值和一个全局最小值,用于测试算法的全局搜索能力。
- 测试函数的作用:
- 通过在标准的测试集上评估算法表现,可以进行算法之间的比较、选择最佳算法或进一步发展改进现有算法。
- 理解测试函数性质有助于设计者开发出更适合解决特定实际问题的定制优化策略。
- 基准测试函数的特性:
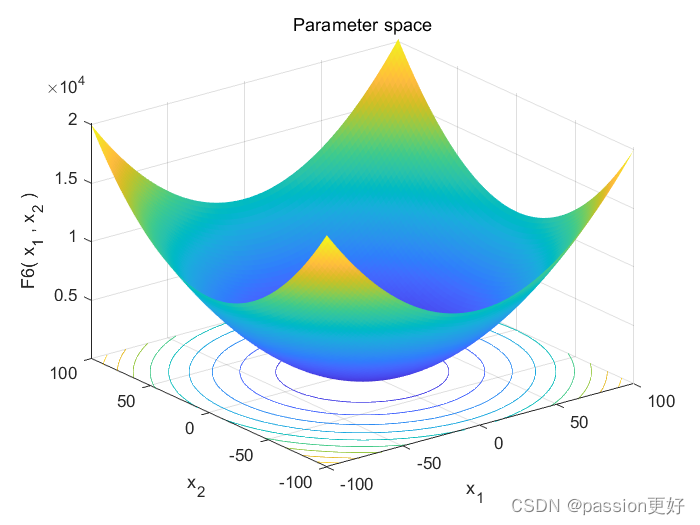
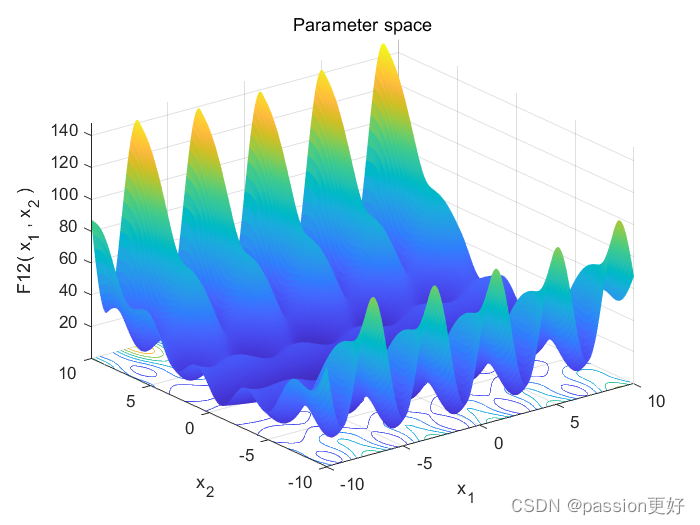
- 这些测试函数在复杂性上有所不同,其形状各异,有些呈现为平滑曲面,有些则充满尖峰和陡峭的谷地。
- 在实际应用中,优化算法通常要面对更为复杂的问题,如动态环境、噪音干扰、不同的目标函数及其它实际约束。因此,尽管这些测试函数提供了一个有益的标准评价体系,但最终算法的有效性仍然需要在真实世界的问题上进行验证。
| basis function | dimension | realm | optimal solutionfmin | |
| F1=Sphere | 30 | [-100,100]n | 0 | |
| F2=Schwefel2.21 | 30 | [-10,10]n | 0 | |
| F3 = Schwefel 1.2 | 30 | [-100,100]n | 0 | |
| F4 = Schwefel 2.22 | 30 | [-100,100]n | 0 | |
| F5=Rosenbrock | 30 | [-30,30]n | 0 | |
| F6=Step | 30 | [-100,100]n | 0 | |
| F7=Quartic | 30 | [-1.28,1.28]n | 0 | |
| F8=Griewank | 30 | [-500,500]n | -12569.5 | |
| F9=Rastrigin | 30 | [-5.12,5.12]n | 0 | |
| F10=Ackley | 30 | [-32,32]n | 0 | |
| F11=Weierstrass | 30 | [-600,600]n | 0 | |
| F12=Schwefel2.26 | 30 | [-50,50]n | 0 | |