1.填充每个节点的下一个右侧节点指针
116. 填充每个节点的下一个右侧节点指针 - 力扣(LeetCode)
方法一:层次遍历
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
// 初始化队列同时将第一层节点加入队列中,即根节点
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
// 外层的 while 循环迭代的是层数
while (!queue.isEmpty()) {
// 记录当前队列大小
int size = queue.size();
// 遍历这一层的所有节点
for (int i = 0; i < size; i++) {
// 从队首取出元素
Node node = queue.poll();
// 连接
if (i < size - 1) {
node.next = queue.peek();
}
// 拓展下一层节点
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
// 返回根节点
return root;
}
}方法二:使用已建立的 next 指针(用时更短)
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
// 从根节点开始
Node leftmost = root;
while (leftmost.left != null) {
// 遍历这一层节点组织成的链表,为下一层的节点更新 next 指针
Node head = leftmost;
while (head != null) {
// CONNECTION 1
head.left.next = head.right;
// CONNECTION 2
if (head.next != null) {
head.right.next = head.next.left;
}
// 指针向后移动
head = head.next;
}
// 去下一层的最左的节点
leftmost = leftmost.left;
}
return root;
}
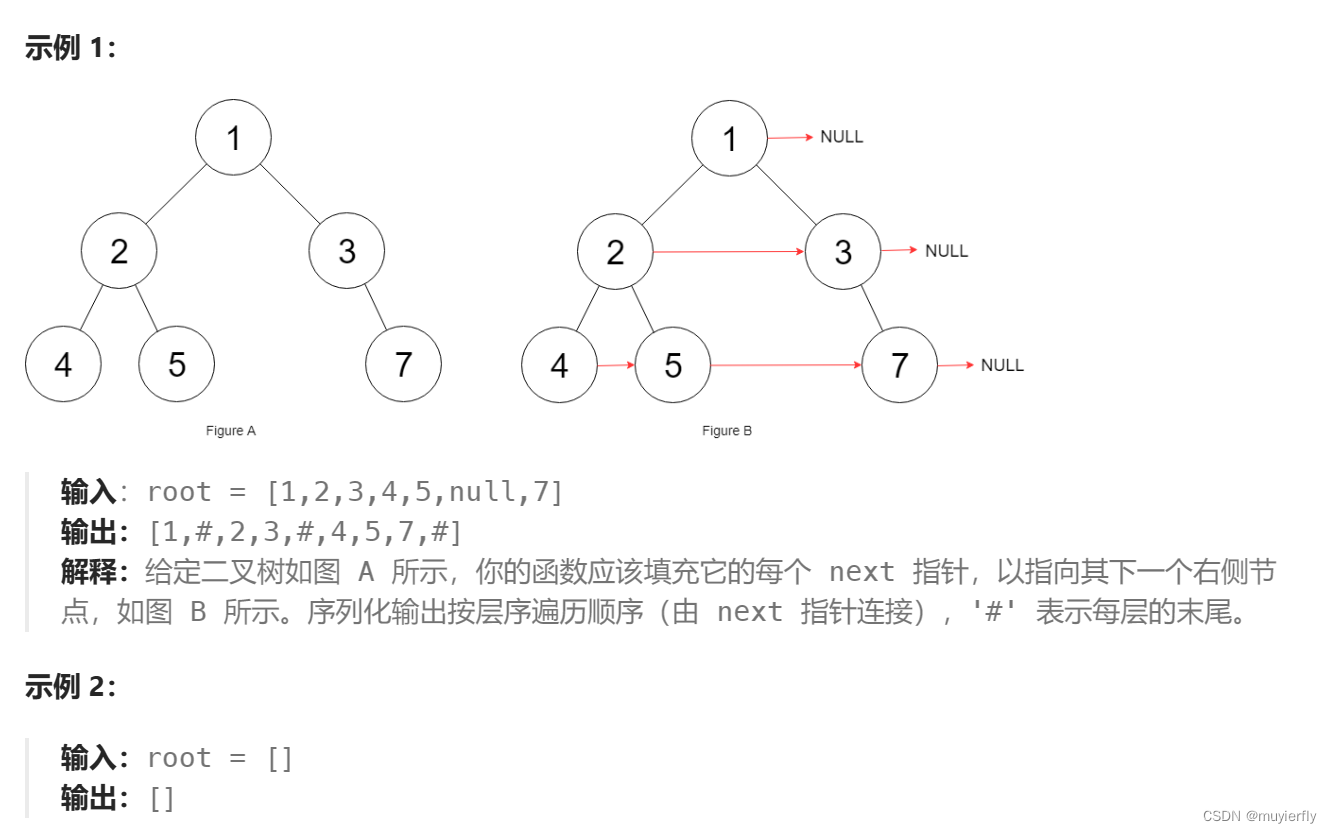
}2.填充每个节点的下一个右侧节点指针2
117. 填充每个节点的下一个右侧节点指针 II - 力扣(LeetCode)

方法一:层次遍历
class Solution {
public Node connect(Node root) {
if (root == null) {
return null;
}
Queue<Node> queue = new ArrayDeque<Node>();
queue.offer(root);
while (!queue.isEmpty()) {
int n = queue.size();
Node last = null;
for (int i = 1; i <= n; ++i) {
Node f = queue.poll();
if (f.left != null) {
queue.offer(f.left);
}
if (f.right != null) {
queue.offer(f.right);
}
if (i != 1) {
last.next = f;
}
last = f;
}
}
return root;
}
}方法二:使用已建立的 next 指针
class Solution {
Node last = null, nextStart = null;
public Node connect(Node root) {
if (root == null) {
return null;
}
Node start = root;
while (start != null) {
last = null;
nextStart = null;
for (Node p = start; p != null; p = p.next) {
if (p.left != null) {
handle(p.left);
}
if (p.right != null) {
handle(p.right);
}
}
start = nextStart;
}
return root;
}
public void handle(Node p) {
if (last != null) {
last.next = p;
}
if (nextStart == null) {
nextStart = p;
}
last = p;
}
}
3.杨辉三角
118. 杨辉三角 - 力扣(LeetCode)
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> ret = new ArrayList<>();
List<Integer> list = new ArrayList<>();
list.add(1);
ret.add(list);
for (int i = 1; i < numRows; i++) {
List<Integer> curRow = new ArrayList<>();
curRow.add(1);
//处理中间的数字
List<Integer> preRow = ret.get(i-1);
for (int j = 1; j < i; j++) {
int val = preRow.get(j) + preRow.get(j-1);
curRow.add(val);
}
//最后一个数字1
curRow.add(1);
ret.add(curRow);
}
return ret;
}
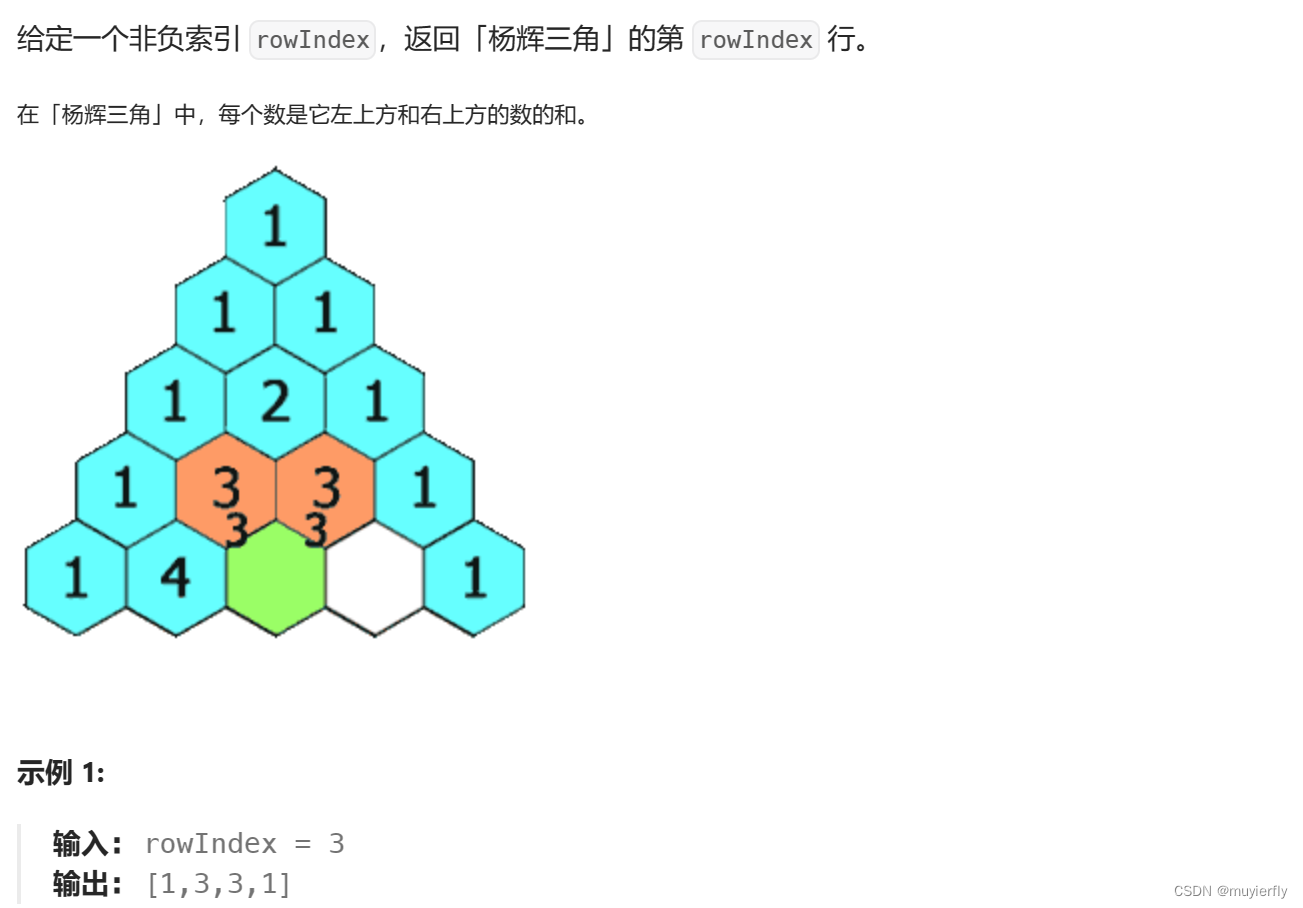
}4.杨辉三角2
119. 杨辉三角 II - 力扣(LeetCode)
方法一:递推
class Solution {
public List<Integer> getRow(int rowIndex) {
List<Integer> row = new ArrayList<Integer>();
row.add(1);
for (int i = 1; i <= rowIndex; ++i) {
row.add(0);
for (int j = i; j > 0; --j) {
row.set(j, row.get(j) + row.get(j - 1));
}
}
return row;
}
}
5.三角形最小路径和
120. 三角形最小路径和 - 力扣(LeetCode)
给定一个三角形
triangle,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标
i,那么下一步可以移动到下一行的下标i或i + 1。
 方法一:动态规划
方法一:动态规划
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[][] f = new int[n][n];
f[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; ++i) {
f[i][0] = f[i - 1][0] + triangle.get(i).get(0);
for (int j = 1; j < i; ++j) {
f[i][j] = Math.min(f[i - 1][j - 1], f[i - 1][j]) + triangle.get(i).get(j);
}
f[i][i] = f[i - 1][i - 1] + triangle.get(i).get(i);
}
int minTotal = f[n - 1][0];
for (int i = 1; i < n; ++i) {
minTotal = Math.min(minTotal, f[n - 1][i]);
}
return minTotal;
}
}