1、信号生成与预处理--剔除异常值简介

在信号生成和预处理过程中，有时候需要剔除异常值（outliers）以确保信号数据的准确性和可靠性。MATLAB提供了一些方法来识别和去除异常值，以下是一些常用的方法：

1. 箱线图检测异常值： 使用箱线图（boxplot）可以可视化数据的分布，并且明显显示出异常值。可以通过计算上下四分位数和异常值的定义来识别和标记异常值。

2. Z-Score方法： Z-Score方法是一种统计方法，可以衡量每个数据点与数据集的平均值的标准偏差之间的距离。通常情况下，如果Z-Score大于某个阈值（如3），则可以将数据点视为异常值。

3. Grubbs检验： Grubbs检验是一种统计测试，用于鉴别数据集中的异常值。它基于假设数据是正态分布的前提进行计算。

4. Hampel滤波器： Hampel滤波器是一种非参数方法，结合了中值滤波和标准差方法，可以有效地识别和剔除异常值。

一旦识别出异常值，可以采取以下方法来处理异常值：

• 替换异常值为数据集的均值、中位数或者上下限值
• 删除异常值
• 使用插值方法进行填充异常值

在MATLAB中，可以使用各种统计工具箱函数来实现异常值的识别和处理，以确保信号数据的准确性和可靠性。

2、语法

说明：对输入向量x应用Hampel滤波器来检测和去除异常值。

1）y = hampel(x)  参数：x：输入信号   y:预处理的输出信号

对于x的每个样本，函数计算由样本及其周围的六个样本组成的窗口的中位数，每边三个。它还使用中位数绝对偏差估计每个样本关于其窗口中位数的标准偏差。如果样本与中位数相差超过三个标准差，则将其替换为中位数。如果x是一个矩阵，那么该函数将x的每一列视为一个独立的通道。

2）[y,j] = hampel(x)  参数：x：输入信号  y:预处理的输出信号  j:离群指数(0/1表示，1离群)

返回一个逻辑矩阵，该矩阵在标识为离群值的所有点的位置为真

3）[y,j,xmedian,xsigma] = hampel(x) 

参数： x：输入信号  y:预处理的输出信号  j:离群指数(0/1表示，1离群)  xmedian：中位数 xsigma：估计标准差

返回x的每个元素的局部中位数和估计标准差。

4）y = hampel(x,k)  参数：x：输入信号   y:预处理的输出信号  k:样本两侧数据数

指定测量窗口中x的每个样本两侧的邻居k的数量。K默认为3。

5）y = hampel(x,k,nsigma)

指定若干个标准差，x的样本必须与局部中位数不同，才能被替换为中位数。sigma默认为3。

3、单通道信号生成与预处理 

0）简介

单通道信号生成与预处理是指在处理和分析信号时只涉及到一个通道（例如有限元仿真数据、传感器数据等），需要对这个单通道信号进行生成和预处理的过程。这种处理通常在单通道数据采集、实时监测、信号处理等领域广泛应用。

在单通道信号生成方面，可以通过不同的方式生成单通道信号来进行后续的处理和分析，例如生成正弦波、方波、脉冲等基本信号，或者根据特定算法生成复杂的信号模型。

在单通道信号预处理方面，通常需要进行以下步骤：

1. 信号生成：根据实际需求生成单通道信号数据，可以是仿真数据、传感器数据等。
2. 数据导入：将生成的单通道信号数据导入到MATLAB中进行处理。
3. 异常值处理：识别并剔除异常值，以确保数据的准确性。
4. 滤波处理：对数据进行滤波操作，去除噪音并平滑数据。
5. 信号分析：对信号进行分析和处理，例如频谱分析、时域分析等。
6. 特征提取：提取信号中的重要特征，为后续的应用提供有用信息。

单通道信号生成与预处理是信号处理过程中的重要环节，在实际应用中常常需要对信号进行适当的处理与分析，提取出有效信息以实现特定的任务。MATLAB提供了丰富的信号处理工具和函数，可以帮助进行单通道信号生成和预处理的操作。通过合适的处理方法，可以提高信号数据的准确性和可靠性，实现对信号的有效处理和分析。

1）单通道信号生成

代码

x = sin(4*pi*(0:199)/200);%输入值
x(6) = 2.5;%异常点1
x(20) = -3;%异常点2
x(120) = 2.5;%异常点3
x(180) = -3;%异常点4
n = 1:length(x);
figure(1)
plot(n,x,'color','r')%加入异常数据

视图效果

 2）单通道信号处理：hampel()函数

代码

x = sin(4*pi*(0:199)/200);%输入值
x(6) = 2.5;%异常点1
x(20) = -3;%异常点2
x(120) = 2.5;%异常点3
x(180) = -3;%异常点4
n = 1:length(x);
figure(1)
plot(n,x,'color','r')%加入异常数据
hold on;
[y,j,xmedian,xsigma] = hampel(x,4);
plot(n,y,'^','color','g')%预处理数据
plot(n,xmedian,'^','color','b')%中位数
plot(n,xsigma,'*','color','y')%标准差
a=find(j);%find()函数：返回非零元素 索引
plot(a,x(j),'s','color','k')
legend('异常','预处理','中位数','估计标准差','离群点')

视图效果

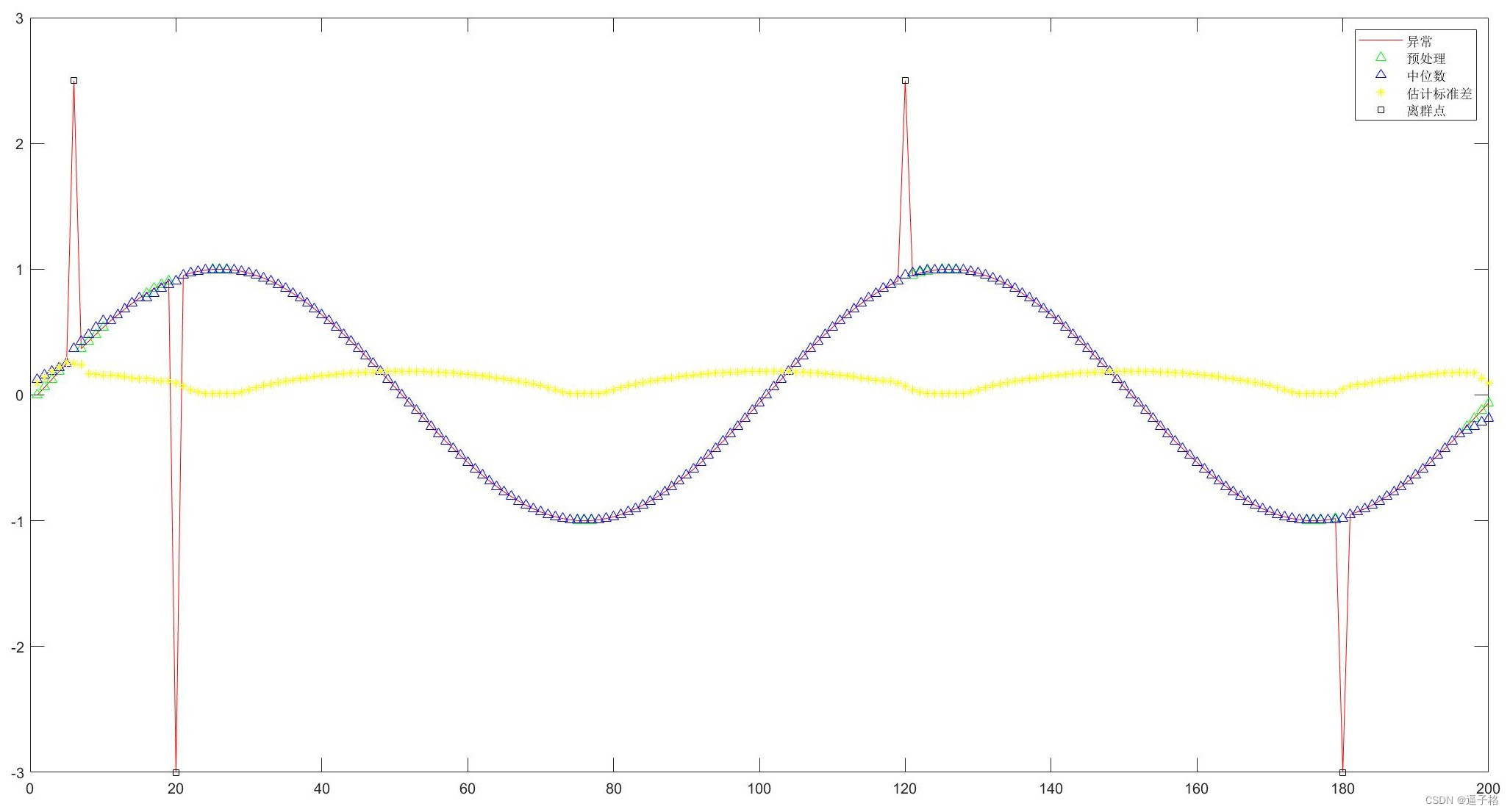
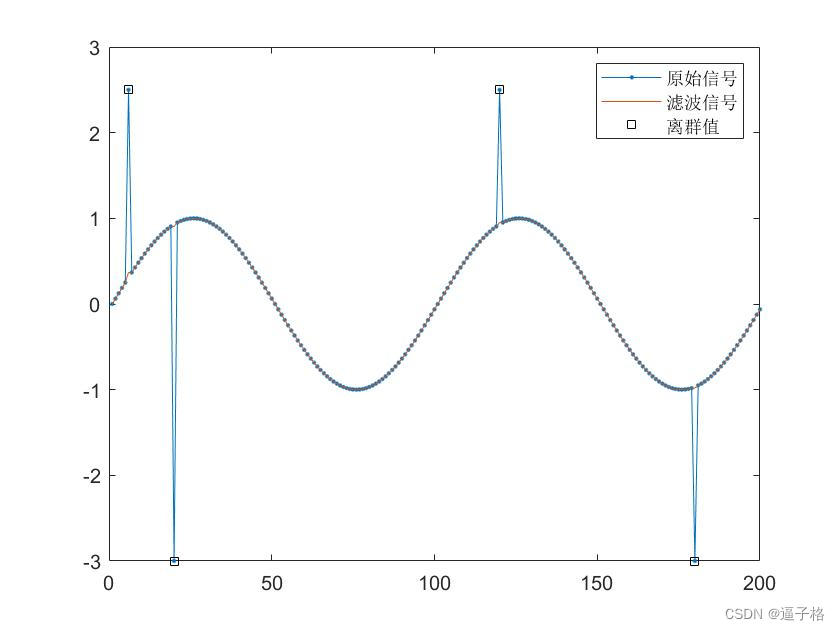
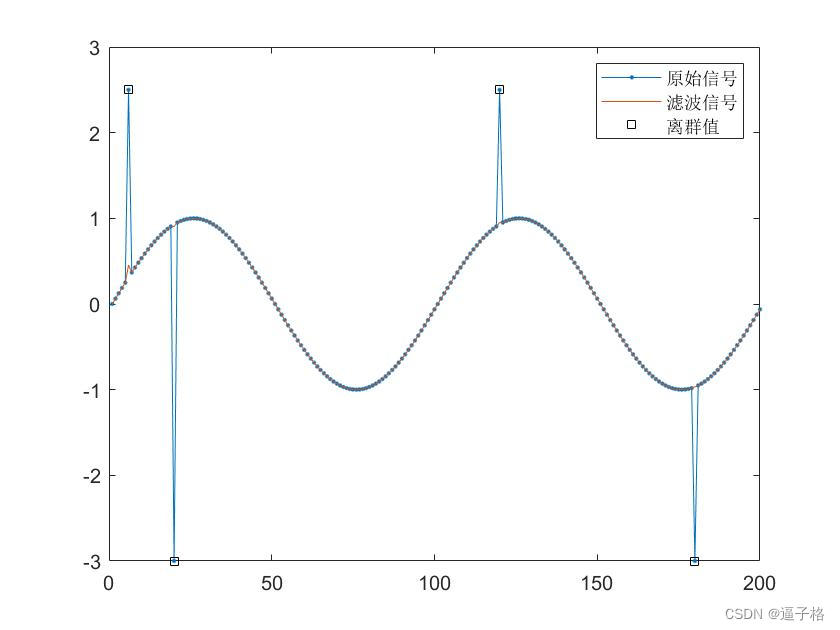
  3）单通道信号处理参数调整

代码

hampel(x,2)%调整k参数

k=2/4/6/8效果图

 

4、双通道信号生成与预处理  

0）简介

双通道信号生成与预处理是指在处理和分析信号时涉及到两个通道（通常是两个独立的采集通道），并且需要对这两个通道的信号进行同步生成和预处理的过程。这种处理通常在双通道数据采集、传感器监测、实验数据采集等领域广泛应用。

在双通道信号生成方面，可以通过不同的方式生成两个通道的信号来进行后续的处理和分析，例如分别生成两个通道的正弦波、方波、脉冲等基本信号，或者根据特定算法生成两个通道的复杂信号。

在双通道信号预处理方面，通常需要进行以下步骤：
1. 数据采集：使用合适的设备采集双通道信号数据。
2. 数据导入：将采集到的双通道信号数据导入到MATLAB中进行处理。
3. 数据校准：校准两个通道的数据，确保其时间对齐和幅度匹配。
4. 异常值处理：识别并剔除异常值，以确保数据的准确性。
5. 滤波处理：对数据进行滤波操作，去除噪音并平滑数据。
6. 信号同步：对两个通道的信号进行同步处理，以便后续分析或可视化。

双通道信号生成与预处理在很多实际应用中都是必不可少的步骤，通过合适的处理方法可以提取有效信息并降低噪声干扰，从而实现对信号数据的准确分析和有效利用。MATLAB提供了丰富的信号处理工具和函数，可以帮助进行双通道信号生成和预处理的操作。

1）双通道信号生成

代码

rng('default')%控制随机函数生成
n = 100;
x = sin(pi./[10 20]'*(1:n)+pi/6)';%双通道信号生成
figure(1)
plot(x)
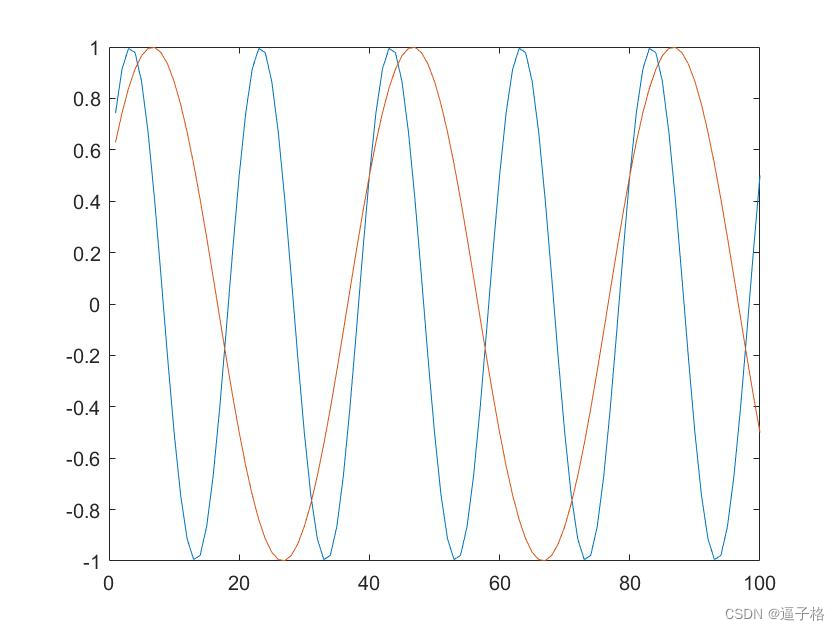
sy= randi(100,9,1);%添加异常参数的索引//100以内,9行1列的矩阵 
x(sy) = x(sy)*2.2;%添加异常参数
x(randi(100,6,1)) = NaN;%添加异常 缺失参数
figure(2)
plot(x)

视图效果

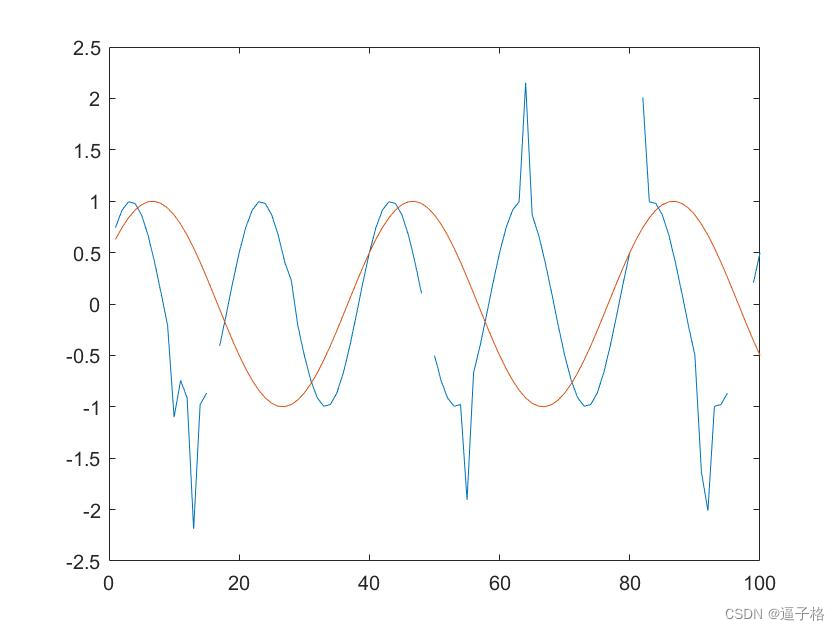
2）双通道信号处理(处理异常点和数据缺失)

代码：

figure(3)
y = hampel(x,4);
plot(y)
figure(4)
[y,j,xmedian,xsigma] = hampel(x,4,2);
plot(y)
hold on
plot(xmedian,'^')

 试图效果

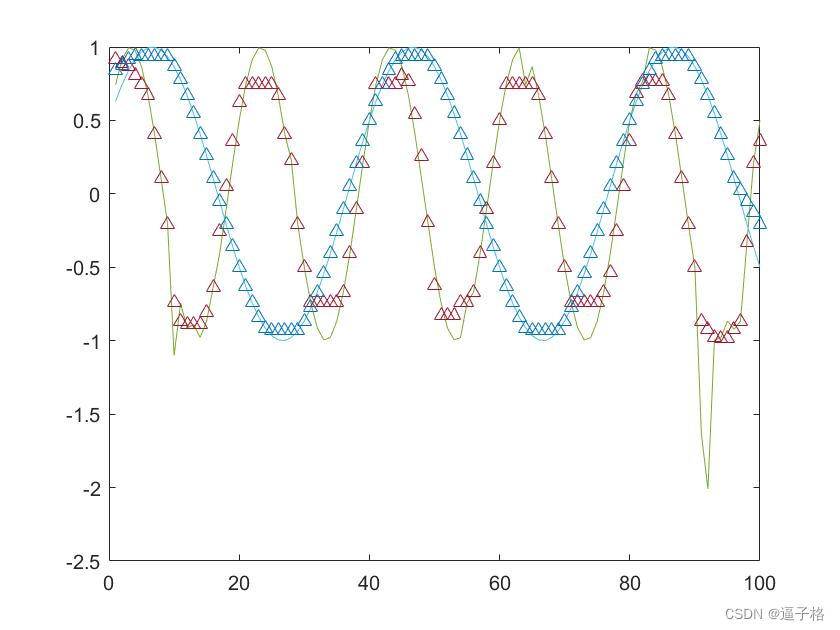
5、总结

在信号生成和预处理过程中，剔除异常值是非常重要的一步，以确保信号数据的准确性和可靠性。在MATLAB中，可以通过一些方法来实现异常值的识别和剔除，以下是一些常用的方法总结：

1. 箱线图检测异常值： 利用boxplot函数绘制箱线图，根据上下四分位数和异常值的定义来识别和标记异常值。

2. Z-Score方法： 计算每个数据点与数据集平均值的标准偏差之间的距离，如果Z-Score大于特定阈值（如3），则将数据点视为异常值。

3. Grubbs检验： 通过Grubbs统计检验法识别数据集中的异常值，基于假设数据服从正态分布的前提进行计算。

4. Hampel滤波器： Hampel滤波器结合了中值滤波和标准差方法，可以有效地识别和剔除异常值。

处理异常值的方法包括替换异常值为数据集的均值、中位数或者上下限值，删除异常值，或者使用插值方法进行填充异常值。

在MATLAB中，可以利用统计工具箱函数实现异常值的识别和处理，确保信号数据的准确性和可靠性。通过剔除异常值，可以提高信号处理的准确性和可靠性，从而更好地分析和应用信号数据。