前言
本系列文章架构概览:
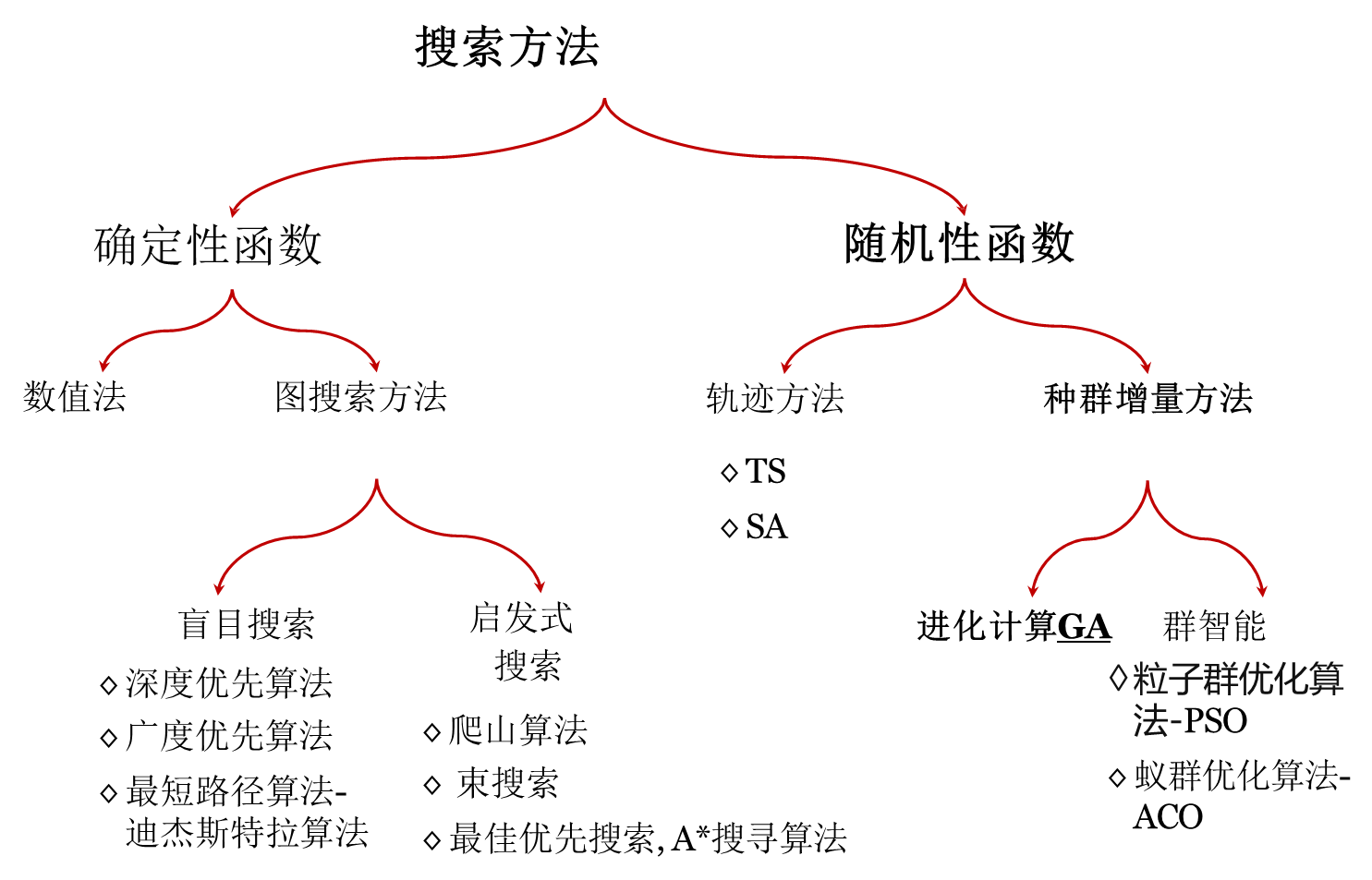
本文将介绍基本遗传算法在解决优化问题中的应用,通过实验展示其基本原理和实现过程:选取一个简单的二次函数作为优化目标,并利用基本遗传算法寻找其在指定范围内的最大值。
2. 基本遗传算法(SGA)
基本遗传算法(Simple Genetic Algorithm : SGA)又称为简单遗传算法,使用选择算子、交叉算子和变异算子这三种基本的遗传算子,操作简单、容易理解,是其它遗传算法的雏形和基础。
2.1 基本遗传算法的构成要素
基本遗传算法由染色体编码方法、适应度函数和遗传算子三个主要要素组成,前文已经对每个要素进行了详细说明:
2.2 算法流程
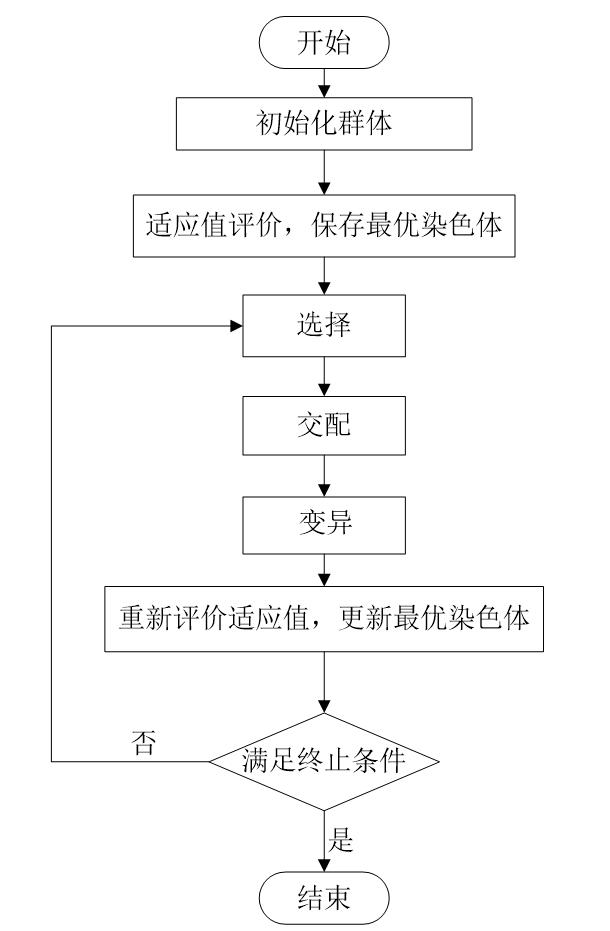
- 初始化种群: 随机生成一定数量的个体,每个个体对应一个可能的解,用二进制或其他编码方式表示。
- 适应度评价: 计算每个个体的适应度,适应度值反映了个体解的优劣程度。
- 选择操作: 根据个体的适应度值,使用一定的选择策略(如轮盘赌选择、锦标赛选择等)从当前种群中选择出一部分个体,作为下一代种群的父代。
- 交叉操作: 对选中的父代个体进行交叉操作,产生新的子代个体。交叉操作通过==重组父代个体的基因==,产生新的解空间。
- 变异操作: 对交叉后的子代个体以一定的小概率进行变异操作,==引入新的基因==,增加种群的多样性。
- 终止条件判断: 检查是否满足算法终止条件(如达到最大迭代次数、找到满意解等),若满足则终止,否则回到步骤2,进行下一代种群的进化。
通过不断重复上述过程,种群中个体的适应度将逐渐提高,最终converge到问题的最优解或近似最优解。
2.3 伪代码
Procedure GeneticAlgorithm()
t = 0 // 初始化迭代次数
InitializePopulation(P(t)) // 初始化种群
Evaluate(P(t)) // 评估种群中个体的适应度
Best = KeepBest(P(t)) // 保留当前最优个体
while (not TerminationConditionMet()) do
P(t) = Selection(P(t)) // 选择操作
P(t) = Crossover(P(t)) // 交叉操作
P(t) = Mutation(P(t)) // 变异操作
t = t + 1 // 更新迭代次数
P(t) = P(t-1)
Evaluate(P(t)) // 重新评估种群中个体的适应度
if (BestIndividual(P(t)) > Best) then
Best = ReplaceBest(P(t)) // 更新最优个体
end if
end while
return Best // 返回找到的最优解
End Procedure
3. 应用到优化问题中
3.1 理论分析
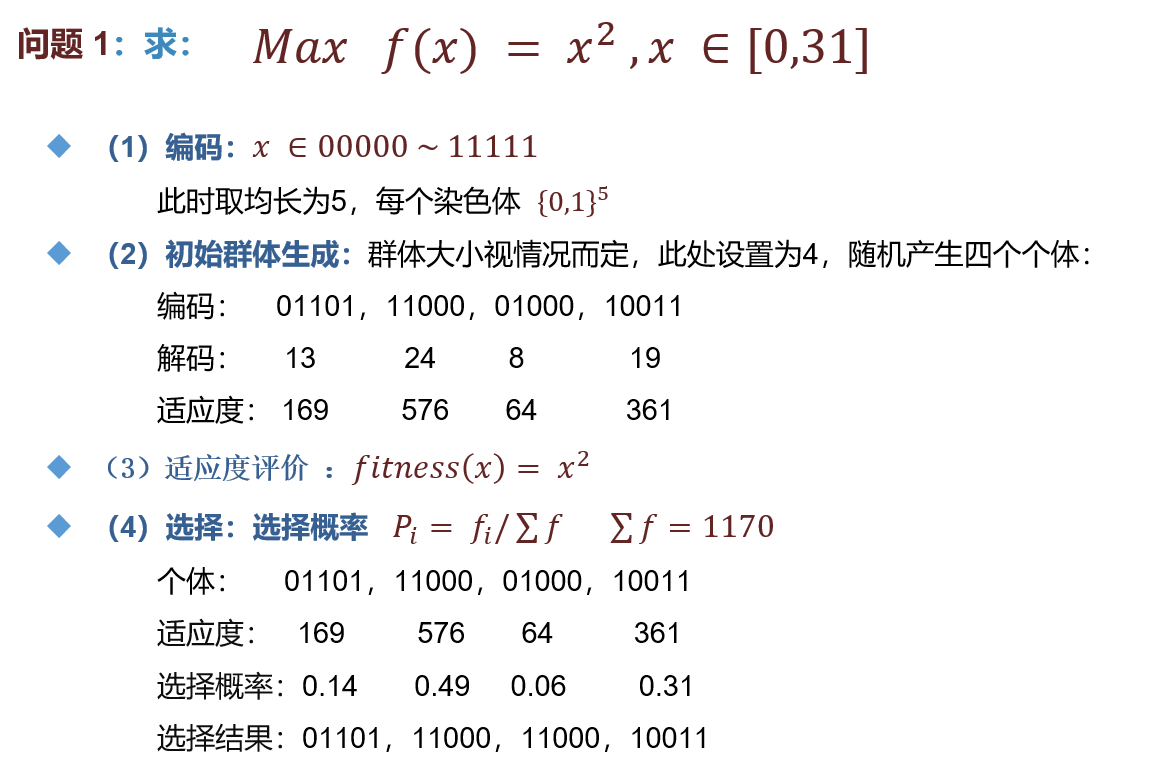
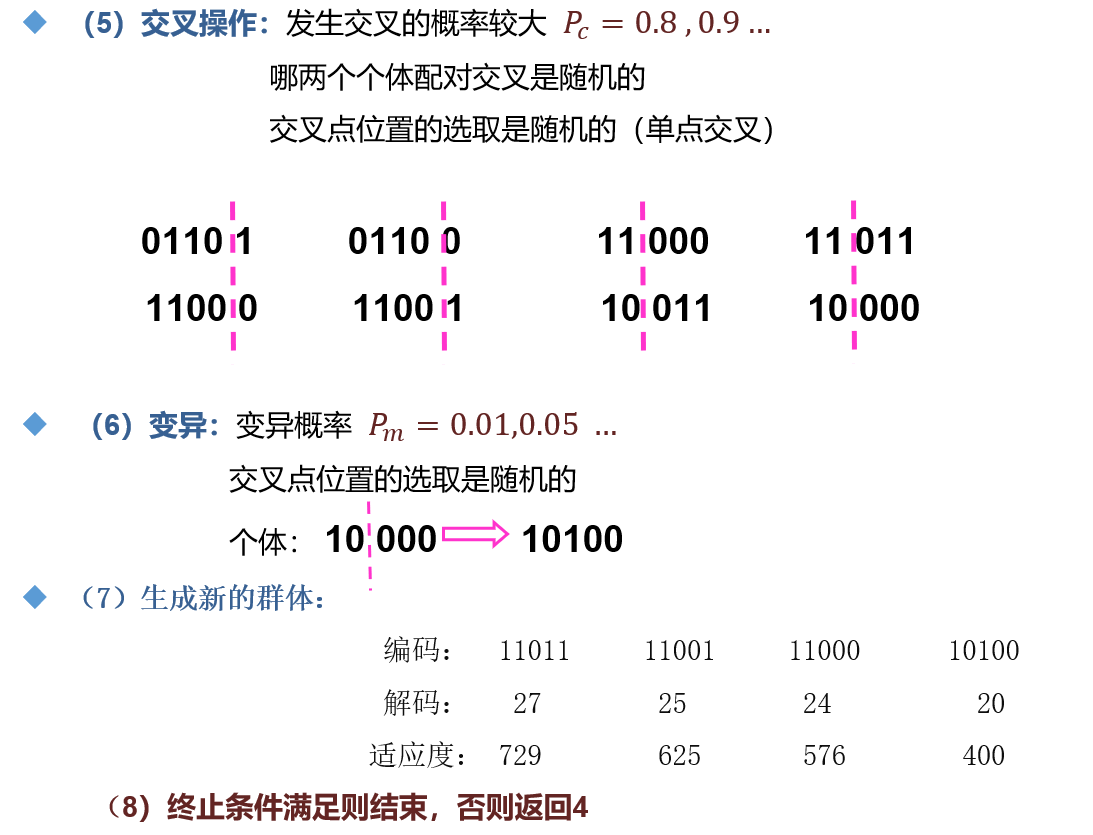
3.2 代码实现
1. 导入所需库
import random
2. 目标函数 f(x)
def f(x):
return x ** 2
3 初始化种群
def initialize_population(population_size, chromosome_length):
return [bin(random.randint(0, 31))[2:].zfill(chromosome_length) for _ in range(population_size)]
生成指定大小的种群,每个个体都是一个长度为 chromosome_length (本实验为5)的二进制字符串,代表一个取值范围在 0 到 31 之间的整数。函数可以拆分为:
def initialize_population(size):
return [encode(random.randint(0, 31)) for _ in range(size)]
- 染色体编码函数 encode(x)
def encode(x):
return bin(x)[2:].zfill(5)
将整数 x 编码成一个长度为 5 的二进制字符串。内置的 bin() 函数将整数转换为二进制字符串,然后使用 zfill() 函数填充到长度为 5。
4. 计算适应度
def evaluate_individual(individual):
x = int(individual, 2)
return f(x)
def evaluate_population(population):
return [evaluate_individual(individual) for individual in population]
evaluate_individual函数计算单个个体的适应度,将个体的二进制编码转换为十进制数x,然后计算目标函数f(x)的值作为适应度;evaluate_population函数遍历整个种群,计算每个个体的适应度,返回一个包含所有个体适应度值的列表。
5. 选择操作:轮盘赌选择
def selection(population, fitness_values):
total_fitness = sum(fitness_values)
# 计算每个个体被选中的概率
probabilities = [fitness / total_fitness for fitness in fitness_values]
# print("\t选择概率: {}".format(probabilities))
selected_population = []
for _ in range(len(population)):
selected_individual = random.choices(population, weights=probabilities)[0]
# print("\t被选个体: {}".format(selected_individual))
selected_population.append(selected_individual)
return selected_population
从轮盘赌选择的机制中可以看到,较优染色体的P值较大,被选择的概率就相对较大。但由于选择过程具有随机性,并不能保证每次选择均选中这些较优的染色体,因此也给予了较差染色体一定的生存空间。
点击【计算智能】遗传算法(二):基本遗传算法在优化问题中的应用【实验】——古月居可查看全文