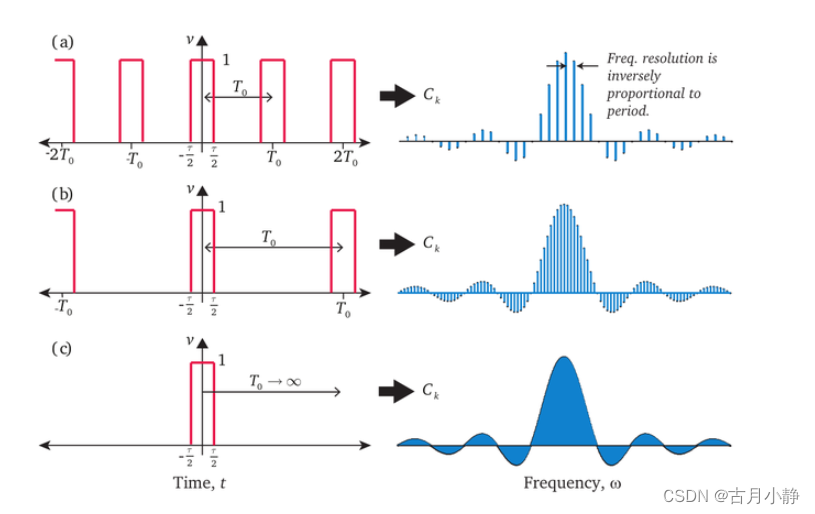
快速算法(FFT),即快速傅里叶变换(Fast Fourier Transform),是一种用于计算离散傅里叶变换(DFT)及其逆变换的高效算法。FFT算法由J.W.库利和T.W.图基于1965年提出,显著减少了计算机计算离散傅里叶变换所需的乘法次数,特别是当被变换的抽样点数N增多时,FFT算法的计算量节省更为显著。以下是关于FFT的详细解析:
一、FFT的基本概念
FFT是一种利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称。它通过将DFT的复杂度从O(n^2)降低到O(nlogn),从而大大提高了计算效率。
二、FFT的应用场景
信号处理:FFT在信号处理领域有广泛应用,如音频、图像和视频处理中的频率分析。
信息学竞赛:在信息学竞赛中,FFT用于加速多项式乘法、高精度大数运算等。
科学计算:在物理、化学、生物等科学领域,FFT也常用于数据分析、模拟仿真等。
三、FFT的基本原理
FFT算法的基本思想是利用DFT的周期性和对称性,通过分治策略将长序列的DFT分解为短序列的DFT,从而减少计算量。具体来说,FFT算法可以分为时间抽取法和频率抽取法两种。
时间抽取法:将输入序列按奇偶分组,然后分别进行DFT,最后通过一定的方式合并结果。这种方法在时域进行抽选,因此称为时间抽取法。
频率抽取法:将DFT的输出按频率的奇偶分组,然后分别计算,最后合并结果。这种方法在频域进行抽选,因此称为频率抽取法。
四、FFT的实现过程
FFT的实现过程通常包括以下几个步骤:
补零操作:如果输入序列的长度不是2的幂次,则需要进行补零操作,使其长度变为最近的2的幂次。
奇偶分离:将输入序列按奇偶分为两部分,分别进行DFT。
递归求解:对分解后的短序列继续进行奇偶分离和DFT计算,直到序列长度为1。
合并结果:根据DFT的性质和递归过程中的计算结果,合并得到最终的DFT结果。
五、FFT的优化
为了提高FFT的计算效率,可以采用多种优化方法,如:
迭代求解:将递归过程转换为迭代过程,减少函数调用和内存消耗。
蝴蝶操作:利用DFT的对称性和周期性,通过蝴蝶操作减少乘法次数。
并行计算:利用现代计算机的并行处理能力,对FFT算法进行并行化实现。
六、FFT的逆变换(IFFT)
IFFT是FFT的逆过程,用于将DFT的结果转换回原始的时域信号。IFFT的算法原理与FFT类似,但在计算过程中需要用到单位根的倒数(即共轭复数)。
七、总结
FFT作为一种高效的离散傅里叶变换算法,在信号处理、信息学竞赛和科学计算等领域有着广泛的应用。通过分治策略和一系列优化方法,FFT能够显著降低计算复杂度,提高计算效率。随着计算机技术的不断发展,FFT算法也在不断完善和优化,以满足更加复杂和多样化的应用需求。