计算机应用数学--第一次作业

第一次作业
- 计算题
- 编程题（20分）

第一次作业

计算题

（20分）求 $E (X)$ ， $Va r (X)$

（1） $X$ 服从 $[a, b]$ 均匀分布。

（2） $X=x_1+x_2+\ldots+x_n,x_i \in \{ 0,1\}$ ，相互独立。

【解】

（1）

随机变量 $X$ 服从 $[a, b]$ 上的均匀分布 $\sim U(a,b)$ ，其概率密度函数为 $f(x)=\frac{1}{b-a}$ ，

期望 $E (X)$ 为：
$\begin{aligned} E(X) &= \int_{-\infty}^{\infty}xf(x)dx \\ &= \int_{a}^{b}\frac{x}{b-a}dx \\ &= F(b)-F(a)\\ &= \frac{a+b}{2} \end{aligned}$
其中 $\frac{x}{b-a}$ 的原函数 $F(x)=\frac{x^2}{b-a}$ ，

同理，可知 $E(X^2) = \frac{a^2+ab+b^2}{3}$ ，

方差 $Va r (X)$ 为：
$\begin{aligned} Var(X) &= E(X-E(X))^2 \\ &= E(X^2)-E(X)^2 \\ &= \frac{a^2+ab+b^2}{3} - (\frac{a+b}{2})^2 \\ &= \frac{(a-b)^2}{12} \end{aligned}$
（2）

由于 $x_i$ 是二值变量 $x_i \in \{0, 1\}$ ，设 $x_i=1$ 的概率为 $p$ ，
$E(x_i) = 0 \cdot P(x_i = 0) + 1 \cdot P(x_i = 1) = 0 \cdot (1 - p) + 1 \cdot p = p$
由于相互独立，所以 $E (X)$ 为：
$\begin{aligned} E(X) &= E(x_1 + x_2 + \ldots + x_n) \\ &= E(x_1) + E(x_2) + \ldots + E(x_n) \\ &= np \end{aligned}$
因为 $x_i$ 只能是 0 或 1，所以 $x_i^2 = x_i$ ，所以，
$Var(x_i) = E(x_i^2) - (E(x_i))^2 = p - p^2 = p(1 - p)$
由于相互独立，所以 $Va r (X)$ 为：
$\begin{aligned} Var(X) &= Var(x_1 + x_2 + \ldots + x_n) \\ &= Var(x_1) + Var(x_2) + \ldots + Var(x_n) \\ &= np(1 - p) \end{aligned}$

（15分）布隆过滤器(Bloom Filter)是一种空间效率高、查询效率快的数据结构，用于判断一个元素是否属于一个集合。它实质上是一个长度为 $m$ 的 01 数组和 $k$ 个不同的哈希函数构成。在添加元素时，将元素经过 $k$ 个哈希函数得到哈希值，并将数组上这些哈希值位置标记为 1。在查询元素时，将元素经过同样的 $k$ 个哈希函数得到哈希值，若数组上这些哈希值位置都为 1，则说明元素可能在集合中，否则一定不在集合中。布隆过滤器可能会出现误判，但不会出现漏判。假设每个哈希函数都是随机函数，请计算在插入 $n$ 个元素后，布隆过滤器出现误判的概率，即一个不在集合中的元素被判定为在集合中。

【解】

$k$ 个随机的哈希函数的取值集合都是 $\{1,2,3\ldots,m\}$ ，且哈希函数之间相互独立，

对于某个位置，经过 1 个哈希函数不被标记的概率为 $(1-\frac{1}{m})$ ，经过 $k$ 个哈希函数均不被标记的概率是 $(1-\frac{1}{m})^k$ ，即添加一个元素后，某个位置不被标记的概率是 $(1-\frac{1}{m})^k$ 。

那么添加 $n$ 个元素后，某个位置仍不被标记的概率是 $(1-\frac{1}{m})^{kn}$ ，该位置被标记的概率是 $1-(1-\frac{1}{m})^{kn}$ 。

对于误判的元素，即一个不在集合中的元素被判定为在集合中的元素，

被判定为在集合中的元素，需要 $k$ 个哈希函数的值都被标记，所以误判率为 $[1-(1-\frac{1}{m})^{kn}]^k$ 。

（15分）我们有两种硬币：一种是公平的硬币，即抛一次正反的概率均为 1/2；另一种是产生正面朝上的概率为 2/3 的硬币。从两枚硬币中挑出一枚，将这枚硬币掷 $n$ 次。抛多少次足以让我们有 99% 的把握选择了哪种硬币？请写出计算过程。

【解】

要猜测哪个硬币被选中，设置阈值 $t$ 介于 $1/2$ 和 $2/3$ 之间。

如果正面比例小于阈值，则猜测是公平的硬币；否则，猜测是另一种有偏差的硬币。

令随机变量 $H_n$ 为前 $n$ 次掷硬币中正面朝上的次数。

掷硬币足够多的次数，以便如果选择了公平的硬币，则 $P_r(\frac{H_n}{n}>t) \le 0.01$ ，如果选择了有偏差的硬币，则 $P_r(\frac{H_n}{n}<t) \le 0.01$ 。

选择的自然阈值是 $7/12$ ，正好在 $1/2$ 和 $2/3$ 中间。

$H_n$ 是独立伯努利变量的总和，对于公平硬币，每个变量的方差为 $1/4$ ，对于有偏差硬币，每个变量的方差为 $2/9$ 。

使用切比雪夫不等式，对于公平的硬币，
$\begin{aligned} P_r(\frac{H_n}{n}>\frac{7}{12}) &= P_r(\frac{H_n}{n} - \frac{1}{2}>\frac{7}{12} - \frac{1}{2}) \\ &= P_r(H_n-E[H_n] > \frac{n}{12}) \\ &\le P_r(|H_n-E[H_n]| > \frac{n}{12}) \\ &\le \frac{Var[H_n]}{(n/12)^2} \\ &= \frac{n/4}{n^2/144} = \frac{36}{n} \end{aligned}$
对于有偏差的硬币，
$\begin{aligned} P_r(\frac{H_n}{n}<\frac{7}{12}) &= P_r(\frac{2}{3} - \frac{H_n}{n}> \frac{2}{3} -\frac{7}{12}) \\ &= P_r(\frac{2n}{3} - H_n > \frac{n}{12}) \\ &= P_r(E[H_n]- H_n > \frac{n}{12}) \\ &\le P_r(|H_n-E[H_n]| > \frac{n}{12}) \\ &\le \frac{Var[H_n]}{(n/12)^2} \\ &= \frac{2n/9}{n^2/144} = \frac{32}{n} \end{aligned}$
如果最多为 0.01，当 $n\ge3600$ 时满足 99% 的置信度。

由于有偏差硬币的方差小于公平硬币的方差，因此如果将阈值设置得更大一点，达到约 $2-\sqrt2$ ，可以做得更好一些，这在掷 3398 次硬币中给出了 99% 的置信度。

（10分）考虑转移概率矩阵，六个状态分别为 ${0,1,2,3,4,5\}$ ，判断给定马尔可夫链是否存在稳定状态？
$\begin{bmatrix} 1/4 & 1/2 & 0 & 0 & 1/4 & 0 \\ 0 & 1/3 & 1/3 & 1/3 & 0 & 0 \\ 0 & 1/4 & 0 & 1/2 & 0 & 1/4 \\ 0 & 0 & 1/4 & 1/4 & 1/4 & 1/4 \\ 1/3 & 0 & 0 & 0 & 1/3 & 1/3 \\ 1/5 & 1/5 & 2/5 & 1/5 & 0 & 0 \end{bmatrix}$

【方法一】

不可约、非周期的马尔可夫链，有平稳分布存在。

判断不可约。

状态转移图如下：

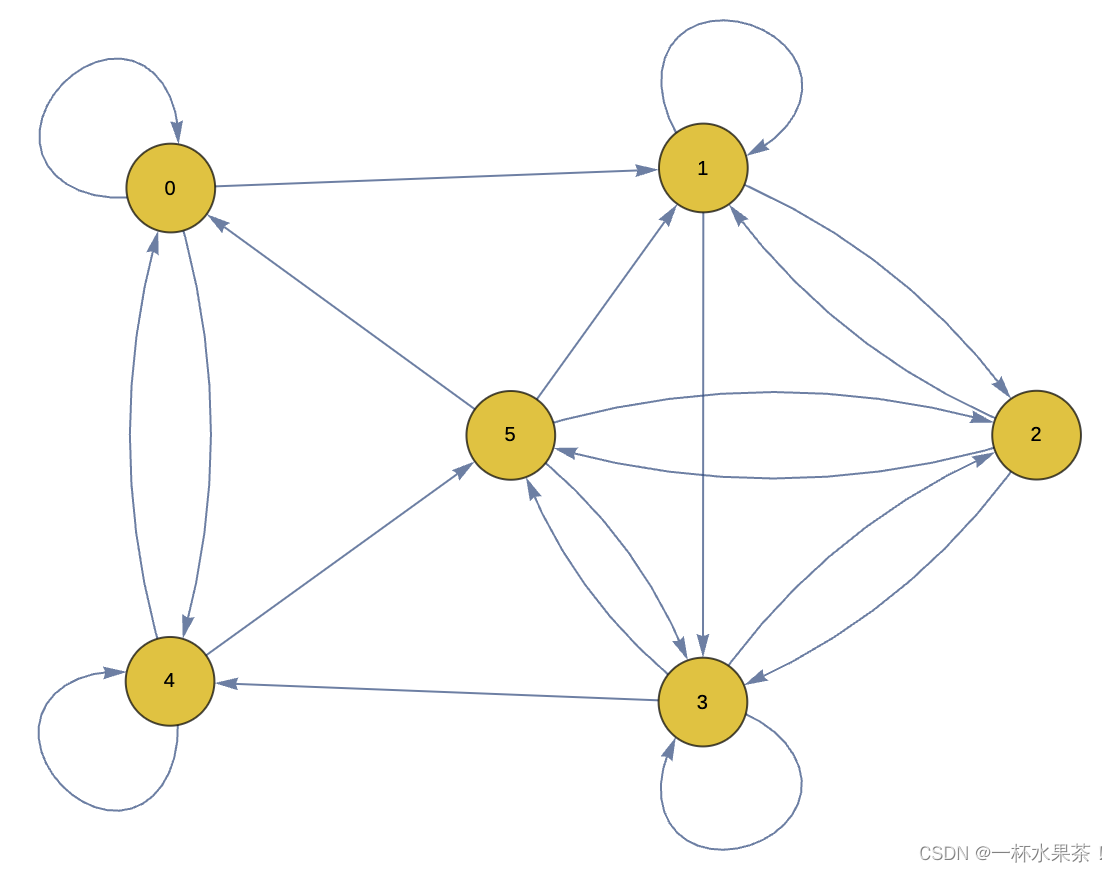
从状态转移图可以看出，存在路径 0->1->2->3->4->5->0，状态 0 可以到达所有的状态，并且可以从所有状态到达。而其他状态都可以到达状态 0，并且可以从状态 0 到达，所以所有的状态都是相互可达的，因此这个马尔可夫链是不可约的。

判断是否为非周期。

对于状态 0，从 0 出发返回 0 的步长可能是 1（0->0），2（0->4->0），3（0->4->4->0），4（0->1->3->5->0），5（0->1->2->3->4->0），6（0->1->2->3->4->4->0）等，其步长的最大公约数为 1，所以状态 0 是非周期的。

对于不可约马尔可夫链，一个非周期状态则说明马尔可夫链是非周期的。

综上，不可约、非周期的马尔可夫链存在平稳分布。

【方法二】

要判断给定的马尔可夫链是否存在稳定状态，需要找到其转移概率矩阵的稳定分布。

设给定的转移概率矩阵为 $P$ ，计算 $P^2,P^3,P^4,P^5,P^6$ ，

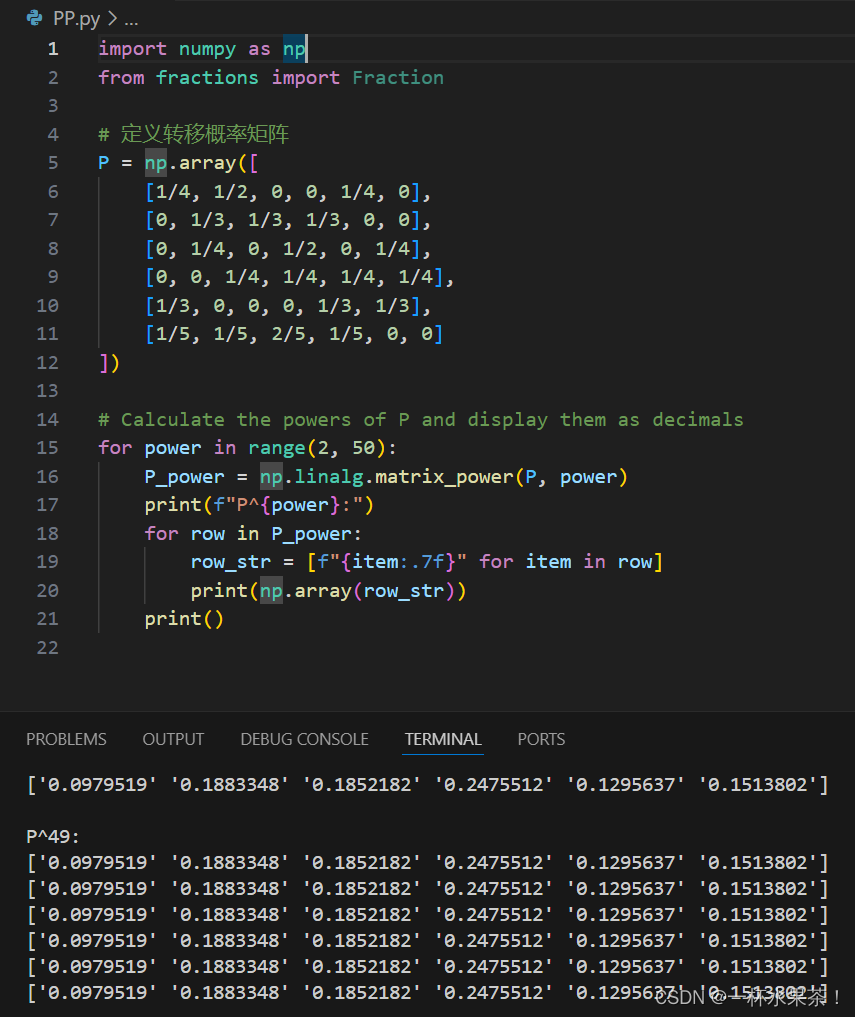
在这里插入图片描述

输出 $P^{49}$ 的值，发现每一行向量都收敛到相同的值，说明该马尔可夫链存在平稳分布。

【方法三】

要确定马尔可夫链是否存在稳定状态，需要检查是否存在一个概率分布向量 $\pi$ ，使得 $\pi P = \pi$ ，其中 $P$ 是给定的转移概率矩阵。

首先，计算该矩阵的特征值和特征向量，以确定是否存在稳定状态。

然后，检查是否存在与特征值 1 对应的特征向量，因为单位特征值对应的特征向量是所需的稳定分布。

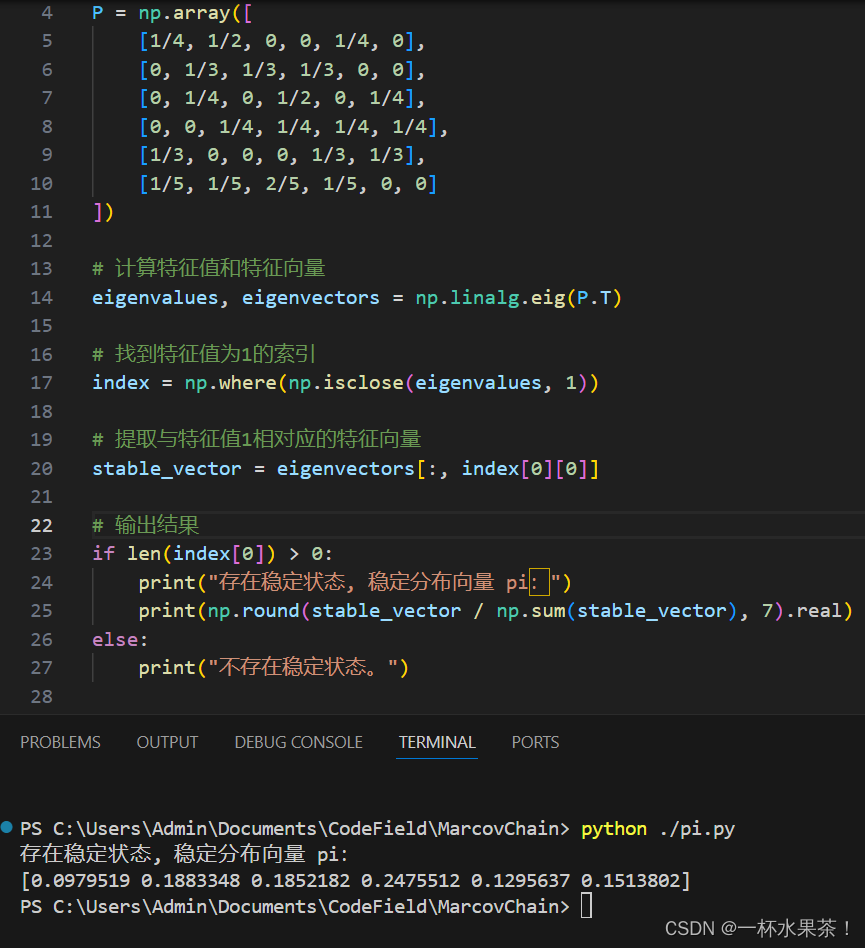
在这里插入图片描述

说明该马尔可夫链存在平稳分布。

（20分） $x_1,\ldots,x_6$ 属性满足以下网络图关系，给出对应的因子图以及联合分布概率公式以及 $x_3$ 的边缘概率公式（即 $P(x_1;x_2;x_3;x_4;x_5;x_6),P(x_3)$ ），对比直接计算 $P(x_3)$ 和使用 Belief Propagation 算法（或称作 Sum-Product Message Passing）的计算代价之间的差异（即比较乘法加法次数)。

【解】

根据网络图，联合分布概率为：
$P(x_1;x_2;x_3;x_4;x_5;x_6)=P(x_1)P(x_2)P(x_3|x_1,x_2)P(x_4|x_2)P(x_5|x_3)P(x_6|x_3)$
Original 因子图如下图：

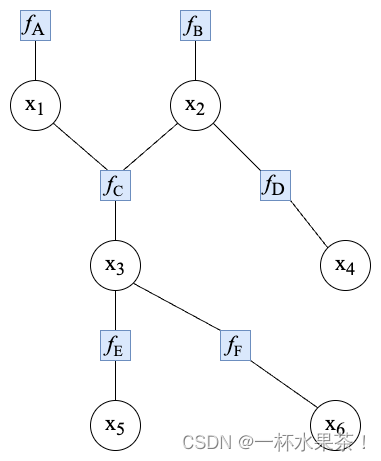
在这里插入图片描述

$x_3$ 的边缘概率为：
$\begin{aligned} P(x_3)&=\sum_{x_1,x_2,...,x_6\ except\ x_3}f_A(x_1)f_B(x_2)f_C(x_1,x_2,x_3)f_D(x2,x4)f_E(x_3,x_5)f_F(x_3,x_6)\\ &=\sum_{x_1}\sum_{x_2}\sum_{x_4}\sum_{x_5}\sum_{x_6}P(x_1)P(x_2)P(x_3|x_1,x_2)P(x_4|x_2)P(x_5|x_3)P(x_6|x_3)\\ &=\left(\sum_{x_5}P(x_5|x_3)\right)\cdot \left(\sum_{x_6}P(x_6|x_3)\right)\cdot \left(\sum_{x_1,x_2}P(x_1)P(x_2)P(x_3|x_1,x_2)\sum_{x_4}P(x_4|x_2)\right)\\ &=m_{f_E\rightarrow x_3}(x_3)m_{f_F\rightarrow x_3}(x_3)\sum_{x_1,x_2}P(x_3|x_1,x_2)P(x_1)P(x_2)m_{f_D\rightarrow x_2}(x_2)\\ &=m_{f_E\rightarrow x_3}(x_3)m_{f_F\rightarrow x_3}(x_3)\sum_{x_1,x_2}P(x_3|x_1,x_2)m_{f_A\rightarrow x_1}(x_1)m_{f_B\rightarrow x_2}(x_2)m_{f_D\rightarrow x_2}(x_2)\\ &=m_{f_E\rightarrow x_3}(x_3)m_{f_F\rightarrow x_3}(x_3)\sum_{x_1,x_2}P(x_3|x_1,x_2)m_{x_1\rightarrow f_C}(x_1)m_{x_2\rightarrow f_C}(x_2)\\ &=m_{f_E\rightarrow x_3}(x_3)m_{f_F\rightarrow x_3}(x_3)m_{f_C\rightarrow x_3}(x_3) \end{aligned}$
假设 $x_i$ 的取值共有 $n(x_i)$ 种，则：

直接计算需要加法 $\sum_{i=1,2,4,5,6}\left(n(x_i)-1\right)$ 次，乘法 $5\times \sum_{i=1,2,4,5,6}n(x_i)$ 。

使用 Belief Propagation 算法，加法仍为 $\sum_{i=1,2,4,5,6}\left(n(x_i)-1\right)$ 次，乘法变为 $2+3\times\sum_{i=1,2}n(x_i)$ 。

编程题（20分）

说明：建议使用开源工具包，例如 scikit-learn 中有朴素贝叶斯函数实现。

朴素贝叶斯分类器（Naive Bayes Classifier）

数据集：Bayesian_Dataset_train.csv, Bayesian_Dataset_test.csv。

数据描述：列名分别为“年纪、工作性质、家庭收入、学位、工作类型、婚姻状况、族裔、性别、工作地点”，最后一列是标签，即收入是否大于50k每年。

任务描述：使用朴素贝叶斯（Naïve Bayesian）预测一个人的收入是否高于50K每年。

要求输出：采用不同评估方式，至少包含两种（如交叉验证和留一法等），给出结果统计，包括Accuracy、precision、recall、F1 score、ROC；

Optional：探索不同参数对结果的影响。

【代码】

import pandas as pd
from sklearn.naive_bayes import GaussianNB
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import cross_val_score, cross_val_predict
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve
import matplotlib.pyplot as plt

# 读取数据
train_data = pd.read_csv('Bayesian_Dataset_train.csv', header=None)
test_data = pd.read_csv('Bayesian_Dataset_test.csv', header=None)

# 将类别特征编码为数值
label_encoder = LabelEncoder()
for i in range(train_data.shape[1]):
    if train_data[i].dtype == 'object':
        train_data[i] = label_encoder.fit_transform(train_data[i])
        test_data[i] = label_encoder.transform(test_data[i])

# 分离特征和标签
X_train, y_train = train_data.iloc[:, :-1], train_data.iloc[:, -1]
X_test, y_test = test_data.iloc[:, :-1], test_data.iloc[:, -1]

# 初始化朴素贝叶斯分类器
naive_bayes = GaussianNB()

# 1. 交叉验证

accuracy_cv = cross_val_score(naive_bayes, X_train, y_train, cv=5, scoring='accuracy').mean()
precision_cv = cross_val_score(naive_bayes, X_train, y_train, cv=5, scoring='precision').mean()
recall_cv = cross_val_score(naive_bayes, X_train, y_train, cv=5, scoring='recall').mean()
f1_cv = cross_val_score(naive_bayes, X_train, y_train, cv=5, scoring='f1').mean()

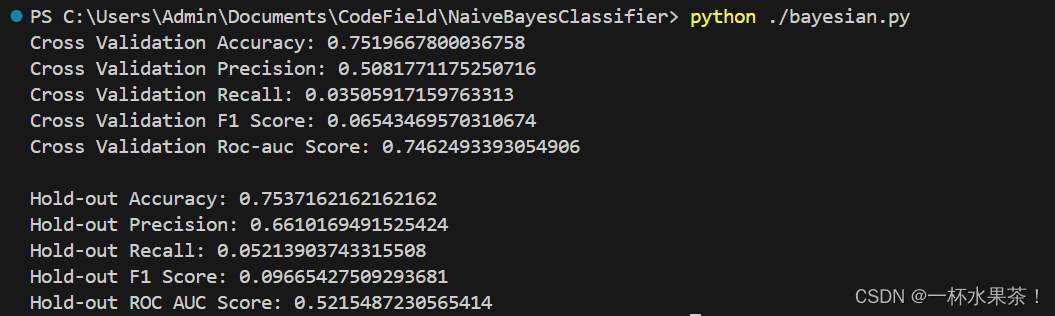
print("Cross Validation Accuracy:", accuracy_cv)
print("Cross Validation Precision:", precision_cv)
print("Cross Validation Recall:", recall_cv)
print("Cross Validation F1 Score:", f1_cv)

y_scores = cross_val_predict(naive_bayes, X_train, y_train, cv=5, method='predict_proba')[:, 1]
fpr_cv, tpr_cv, thresholds_cv = roc_curve(y_train, y_scores)
roc_auc_cv = roc_auc_score(y_train, y_scores)
print("Cross Validation Roc-auc Score:", roc_auc_cv)

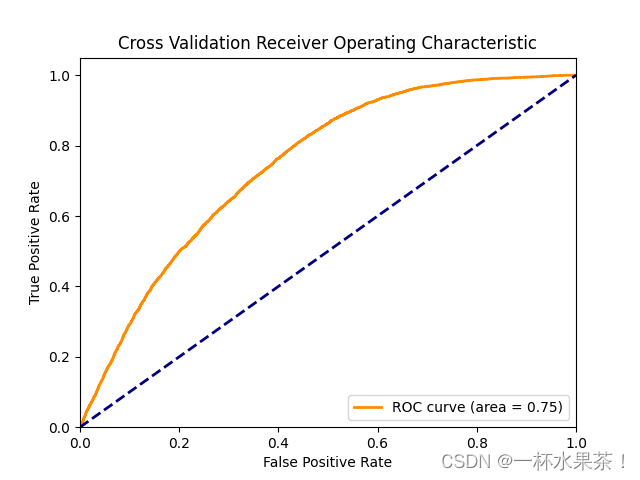
plt.figure()
plt.plot(fpr_cv, tpr_cv, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc_cv)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Cross Validation Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

# 2. 留出法

naive_bayes.fit(X_train, y_train)
y_pred = naive_bayes.predict(X_test)

print(f"\nHold-out Accuracy: {accuracy_score(y_test, y_pred)}")
print(f"Hold-out Precision: {precision_score(y_test, y_pred)}")
print(f"Hold-out Recall: {recall_score(y_test, y_pred)}")
print(f"Hold-out F1 Score: {f1_score(y_test, y_pred)}")
print(f"Hold-out ROC AUC Score: {roc_auc_score(y_test, y_pred)}")


# 获取测试集上的预测概率
y_scores = naive_bayes.predict_proba(X_test)[:, 1]

# 计算 ROC 曲线和 AUC
fpr, tpr, thresholds = roc_curve(y_test, y_scores)
roc_auc = roc_auc_score(y_test, y_scores)

# 绘制 ROC 曲线
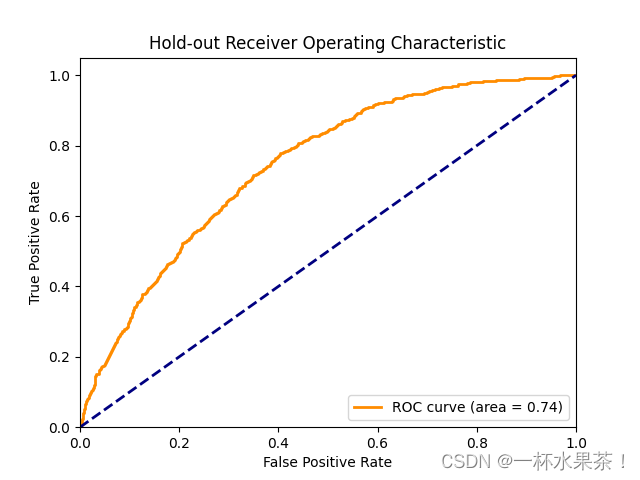
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Hold-out Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()