这是《Attention Is All You Need》通俗解读的第3篇,前文见这里:
《Attention is all you need》通俗解读,彻底理解版:part1
《Attention is all you need》通俗解读,彻底理解版:part2
最近为了撰写这部分内容,将论文又重新通读了一遍,也查阅了一些相关的资料,每阅读一遍资料都有新的收获。
发现Transformer架构的设计思想是真的牛,尤其是当你尝试用数学的思想来解释该架构时。
但是限于目前本人的数学功底还不够扎实(数学是一个非常严谨的学科),预计在未来会恶补一些数学知识,然后再尝试用通俗的数学知识来解析Transformer 架构的思想。
本篇将继续沿着前面几篇解读论文的思路,来解读一下论文中的第3.2.1章节,对应的内容是模型结构的“注意力”部分。
1. 注意力机制
这一部分作者主要将 Transformer 架构中的注意力机制进行了讲述,先看下第一段原文。
An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key。
第一段作者简要介绍了注意力机制是什么。
事实上我在之前写了很多文章来介绍注意力机制,你可以参考小报童专栏以及之后的文章来详细了解。如何理解AI模型的“注意力”?
按照论文中这段的描述,注意力机制可以将 query 和 key-value 对映射到输出上,这里的 query、key、value和输出都是向量。
解释一下这句话:首先模型处理的都是向量,这个向量可以理解为是某个单词(token)的词嵌入表示,关于为什么要将单词token化以及为什么要使用词嵌入表示,在小报童专栏中都有非常详细的介绍,所以你应该可以理解为什么模型处理的都是向量了。
另外,将其映射到输出是什么意思呢?结合下一句来看:输出是由 value 的加权和得到的,而加权里面的权重,则是通过计算 query 和 key 的相似度得到,在你理解了上面的细节之后,对于第一段你应该会理解的非常透彻。
事实上,计算query 和 key 之间的相似度可以有非常多的“相似函数”完成,不同的函数计算的结果肯定不一样,但是作用是相似的。
在3.2.1节,作者介绍了他们使用的计算相似度的函数,以及利用该函数完成注意力的计算。
We call our particular attention "Scaled Dot-Product Attention" (Figure 2). The input consists of queries and keys of dimension dk, and values of dimension dv. We compute the dot products of the query with all keys, divide each by √dk, and apply a softmax function to obtain the weights on the values.
作者把Transformer 中使用的注意力叫做“Scaled Dot-Product Attention”,翻译过来就是“带缩放”的点乘注意力。
点乘很好理解,实际上就是内积运算。在学数学的内积运算时,你可能还记得,两个向量的内积代表了两个向量的相似程度。内积越大,说明两个向量越相似,如果两个向量正交(二维平面垂直)则说明两个向量相关性为零。
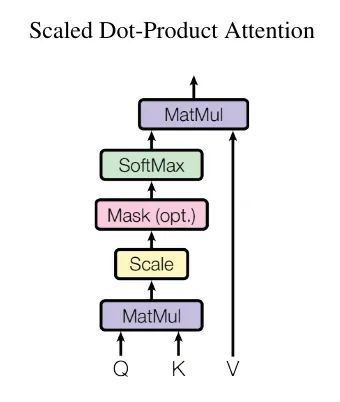
那么“带缩放“是什么意思呢?其实很简单,作者在原本点乘运算的基础上,除以了根号下dk,然后将除之后的结果,输入给softmax(查看 softmax 的原理解析)计算权重。至于为什么要除以根号下dk,这里先放一放,后面再介绍(你可以暂时先简单理解为对计算出来的注意力分数进行缩放即可)。
有几个概念进行下澄清:Q和K的转置直接相乘,结果是两者的相似度,当然你可以可以把它叫做两者的注意力分数,然后将结果除以 √dk 后经过softmax运算,得到的是归一化后的注意力分数,此时的注意力分数便是权重,和V矩阵进行相乘。
下面用一个示意图来表示注意力机制的计算过程。
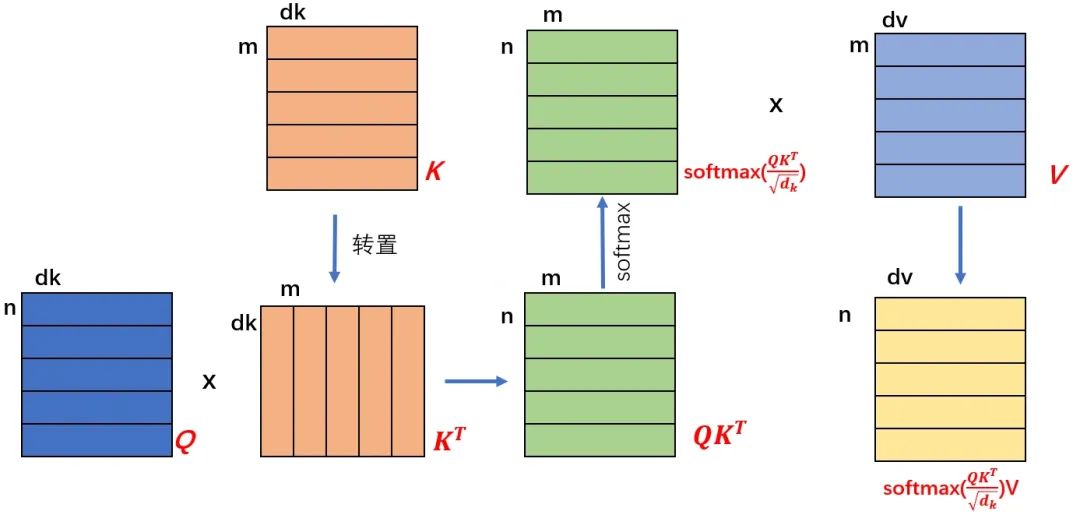
首先,在实际运算时,不论是为了计算的高效,还是为了模型处理数据的方便,总之,都是以矩阵的形式来进行运算。
对于Q,K,V三个向量来说,其矩阵形式则是将多个 token 的词向量在二维平面进行了堆叠展开。
以Q矩阵为例(上图最左下角的矩阵),n 代表 n 个token,dk代表了每个token的词嵌入向量的维度,在论文中dk 取值为512。你可以理解为对于每一个单词token,在这高达 512个维度的词嵌入空间中,存在512特征来表示一个词的语义。
比如可以把cat 表示为[会跑,会爬树,动物,四只腿,两只眼睛,..., 其他AI模型可以识别但人类可能无法理解的可以描述猫的特征]。总之,用512个特征就可以非常充分的描述cat这个单词的语义。
根据公式,首先计算 Q 和 K 的转置的矩阵运算,得到一个 n x m 的矩阵。按照矩阵计算相似度的含义,得到的 n x m 的矩阵中的每一个值,代表了 Q 中的第 i 个 token 与 K 中的第 j 个token 的相似程度,然后经过 softmax 计算得到归一化后的相似分数,这个分数就作为权重和 V 矩阵相乘。
当一个权重矩阵和一个值矩阵相乘时,实际上就是对值矩阵以对应的权重系数进行特征提取和融合的过程。这一点在矩阵乘法的本质中有详细的介绍。
因此,相似度分数经过softmax归一化之后得到的权重,和V矩阵相乘,实际上就是对 V 矩阵的特征进行提取。
V矩阵中的特征是什么呢,其实也是每个token的描述特征,就类似于上文描述cat那样。对其中感兴趣的特征进行提取和融合,不感兴趣的特征可能置为0或直接丢弃,得到的结果就是从V矩阵中提取和融合之后的特征。
这就是注意力机制(或者叫做带缩放的点乘注意力机制)的计算过程。
看到这你可能还不能完全理解这个计算过程在真实世界中的含义,因为整个过程涉及的步骤是各种矩阵乘法,因此需要对矩阵乘法有非常深刻的理解才可以更好的了解这部分的真实含义,并且原始论文也没有针对为什么这么做给出过多的解释。
要更加深入的理解这部分内容,需要不断探究每一步运算的本质和动机,这部分是整个Transformer 架构的核心内容,后面我会一步步将上述计算过程的每一次矩阵运算进行拆解,以期望可以完全理解该架构的设计思路。
至于看完本节内容,你只需要理解上述的文字部分和“注意力机制”的大体计算过程就可以了。
更多细节请持续关注后续的文章,在将注意力机制的运算有了非常深刻的理解之后,多头注意力以及其他的算法都会变得相对简单。
我的技术专栏已经有几百位朋友加入了。
如果你也希望了解AI技术,学习AI视觉或者大语言模型,戳下面的链接加入吧,这可能是你学习路上非常重要的一次点击呀
CV视觉入门第三版(细化版)完成
我的Transformer专栏努力更新中
最后,送一句话给大家:生活不止眼前,还有诗和远方,共勉~