目录
Neutral Controls
Noise Inducing Control
Feature Selection: A Bias-Variance Trade-Off
Neutral Controls
现在,您可能已经对回归如何调整混杂变量有了一定的了解。如果您想知道干预 T 对 Y 的影响,同时调整混杂变量 X,您所要做的就是在模型中加入 X。或者,为了得到完全相同的结果,您可以根据 X 预测 T,得到残差,并将其作为干预的去势版本。在 X 固定不变的情况下,将 Y 与这些残差进行回归,就能得到 T 与 Y 的关系。
但 X 中应包含哪些变量呢?同样,并不是因为增加变量就能调整变量,所以你想在回归模型中包含所有变量。你不想包含共同效应(对撞机)或中介变量,因为这些变量会引起选择偏差。但在回归中,您还应该了解更多类型的控制因素。这些控制项乍看起来似乎无害,但实际上却相当有害。这些控制被称为中性控制,因为它们不会影响回归估计的偏差。但它们会对方差产生严重影响。正如您所看到的,在回归中包含某些变量时,需要权衡偏差和方差。例如,请考虑下面的 DAG:

您是否应该在模型中加入 credit_score2?如果不包括它,就会得到一直以来看到的相同结果。这个结果是无偏的,因为您是根据信用评分 1_buckets 进行调整的。但是,尽管您不需要这样做,请看看如果您将 credit_score2 计算在内会发生什么。将下面的结果与您之前得到的不包含 credit_score2 的结果进行比较。有什么变化?
formula = "default~credit_limit+C(credit_score1_buckets)+credit_score2"
model = smf.ols(formula, data=risk_data_rnd).fit()
model.summary().tables[1]首先,关于信贷限额的参数估计值变高了一些。但更重要的是,标准误差减小了。这是因为 credit_score2 对结果 Y 有很好的预测作用,它将有助于线性回归的去噪步骤。在 FWL 的最后一步,由于包含了 credit_score2,Y 的方差将减小,对 T 进行回归将得到更精确的结果。
这是线性回归的一个非常有趣的特性。它表明,线性回归不仅可以用来调整混杂因素,还可以用来减少噪音。例如,如果您的数据来自适当随机化的 A/B 测试,您就不需要担心偏差问题。但您仍然可以使用回归作为降噪工具。只需包含对结果有高度预测性的变量(并且不会引起选择偏差)即可。
Noise Inducing Control
就像控制可以减少噪音一样,它们也可以增加噪音。例如,再次考虑条件随机实验的情况。但这次,您感兴趣的是信用额度对消费的影响,而不是对风险的影响。和上一个例子一样,信用额度是随机分配的,给定的是 credit_score1。但这次,我们假设credit_score1 不是混杂因素。它是干预的原因,但不是结果的原因。这个数据生成过程的因果图如下所示:

这意味着您不需要对credit_score1 进行调整,就能得到信用额度对消费的因果效应。单变量回归模型就可以了。在这里,我保留了平方根函数,以考虑干预反应函数的凹性:
spend_data_rnd = pd.read_csv("data/spend_data_rnd.csv")
model = smf.ols("spend ~ np.sqrt(credit_limit)",
data=spend_data_rnd).fit()
model.summary().tables[1]
但是,如果你确实包括了credit_score1_buckets,会发生什么呢?
model = smf.ols("spend~np.sqrt(credit_limit)+C(credit_score1_buckets)",
data=spend_data_rnd).fit()
model.summary().tables[1]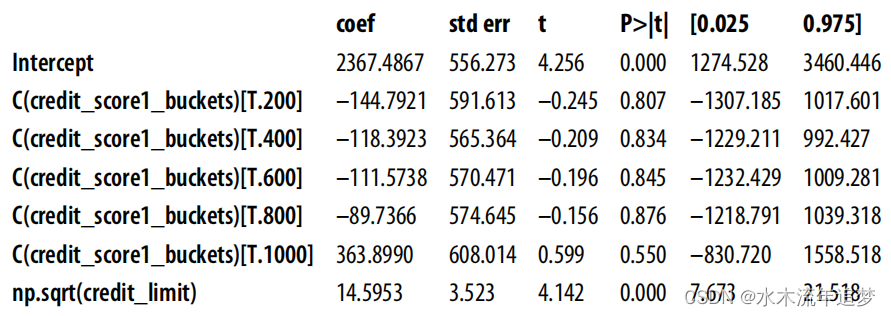 您可以看到,它增加了标准误差,扩大了因果参数的置信区间。这是因为,OLS 喜欢干预方差大的情况。但是如果控制了一个可以解释干预的协变量,就会有效地降低干预的方差。
您可以看到,它增加了标准误差,扩大了因果参数的置信区间。这是因为,OLS 喜欢干预方差大的情况。但是如果控制了一个可以解释干预的协变量,就会有效地降低干预的方差。
Feature Selection: A Bias-Variance Trade-Off
在现实中,很难出现协变量导致干预而不导致结果的情况。最有可能出现的情况是,有很多混杂因素同时导致 T 和 Y,只是程度不同而已。在图 中,X1 是 T 的强致因,但 Y 的弱致因;X3 是 Y 的强致因,但 T 的弱致因;X2 处于中间位置,如每个箭头的粗细所示。
在这种情况下,您很快就会陷入进退两难的境地。一方面,如果您想摆脱所有偏差,就必须包括所有协变量;毕竟,它们是需要调整的混杂因素。另一方面,对干预原因进行调整会增加你的估计器的方差。
为了了解这一点,让我们根据图 中的因果图来模拟数据。这里,真实的 ATE 是 0.5。如果您试图在控制所有混杂因素的情况下估计这一效应,估计值的标准误差会过高,无法得出任何结论。
np.random.seed(123)
n = 100
(x1, x2, x3) = (np.random.normal(0, 1, n) for _ in range(3))
t = np.random.normal(10*x1 + 5*x2 + x3)
# ate = 0.05
y = np.random.normal(0.05*t + x1 + 5*x2 + 10*x3, 5)
df = pd.DataFrame(dict(y=y, t=t, x1=x1, x2=x2, x3=x3))
smf.ols("y~t+x1+x2+x3", data=df).fit().summary().tables[1]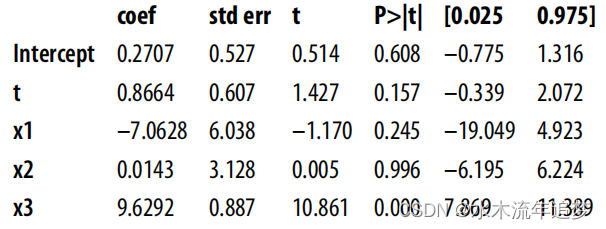
如果您知道其中一个混杂因素对干预的预测作用很强,而对结果的预测作用很弱,您可以选择将其从模型中剔除。在本例中,这就是 X1。现在,请注意!这将使您的估计出现偏差。但是,如果这也能显著降低方差,也许这就是值得付出的代价:
smf.ols("y~t+x2+x3", data=df).fit().summary().tables[1]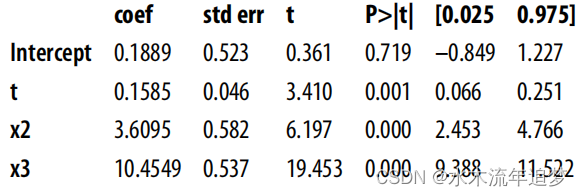
底线是,在模型中包含(调整)的混杂因素越多,因果关系估计值的偏差就越小。但是,如果您包含的变量对干预结果的预测作用较弱,但对治疗的预测作用较强,那么这种偏差的减少将以方差的增加为代价。同理可证,有时为了减少方差而接受一点偏差是值得的。此外,您应该非常清楚,并非所有的混杂因素都是相同的。当然,因为 T 和 Y 的关系,所有的混杂因素都是常见的。但如果它们对治疗的解释太多,而对干预结果的解释几乎没有,那么你真的应该考虑将其从调整中剔除。这适用于回归,但也适用于其他调整策略,如倾向得分加权。
遗憾的是,混杂因素对干预的解释能力应该有多弱,才能证明剔除它是合理的,这在因果推理中仍是一个未决问题。不过,这种偏差与方差的权衡还是值得了解的,因为它有助于您理解和解释线性回归的情况。







![【BUUCTF-PWN】7-[第五空间2019 决赛]PWN5](https://i-blog.csdnimg.cn/direct/fae5708be3dc49ff9957efef258c59c2.png)