栈在括号匹配中的应用
流程图

代码
#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10
typedef struct {
char data[MaxSize];
int top;
} SqStack;
// 初始化栈
void InitStack(SqStack* S) {
S->top = -1; // 初始化栈顶指针
}
// 判空
bool StackEmpty(SqStack* S) {
if (S->top == -1) {
return true;
} else {
return false;
}
}
// 入栈
bool Push(SqStack* S, char x) {
if (S->top == MaxSize - 1) { // 栈满,报错
return false;
} else {
S->top = S->top + 1; // 指针先加1
S->data[S->top] = x; // 新元素入栈
return true;
}
}
// 出栈
bool Pop(SqStack* S, char* x) {
if (StackEmpty(S)) {
return false;
} else {
*x = S->data[S->top]; // 栈顶元素先出栈
S->top = S->top - 1; // 指针减1
return true;
}
}
// 括号匹配检查
bool bracketCheck(char str[], int length) {
SqStack S;
InitStack(&S); // 初始化一个栈
for (int i = 0; i < length; i++) {
if (str[i] == '(' || str[i] == '[' || str[i] == '{') {
Push(&S, str[i]); // 扫描到左括号,入栈
} else {
if (StackEmpty(&S)) { // 扫描到右括号,且当前栈空
return false; // 匹配失败
}
char topElem;
Pop(&S, &topElem); // 栈顶元素出栈
if (str[i] == ')' && topElem != '(') {
return false;
}
if (str[i] == ']' && topElem != '[') {
return false;
}
if (str[i] == '}' && topElem != '{') {
return false;
}
}
}
return StackEmpty(&S); // 检索全部括号后,栈空说明匹配成功
}
int main() {
char str[] = "{([()])}";
int length = sizeof(str) / sizeof(str[0]) - 1; // 计算字符串长度,减1是为了去掉结尾的'\0'
if (bracketCheck(str, length)) {
printf("括号匹配成功\n");
} else {
printf("括号匹配失败\n");
}
return 0;
}
栈在表达式求值中的应用
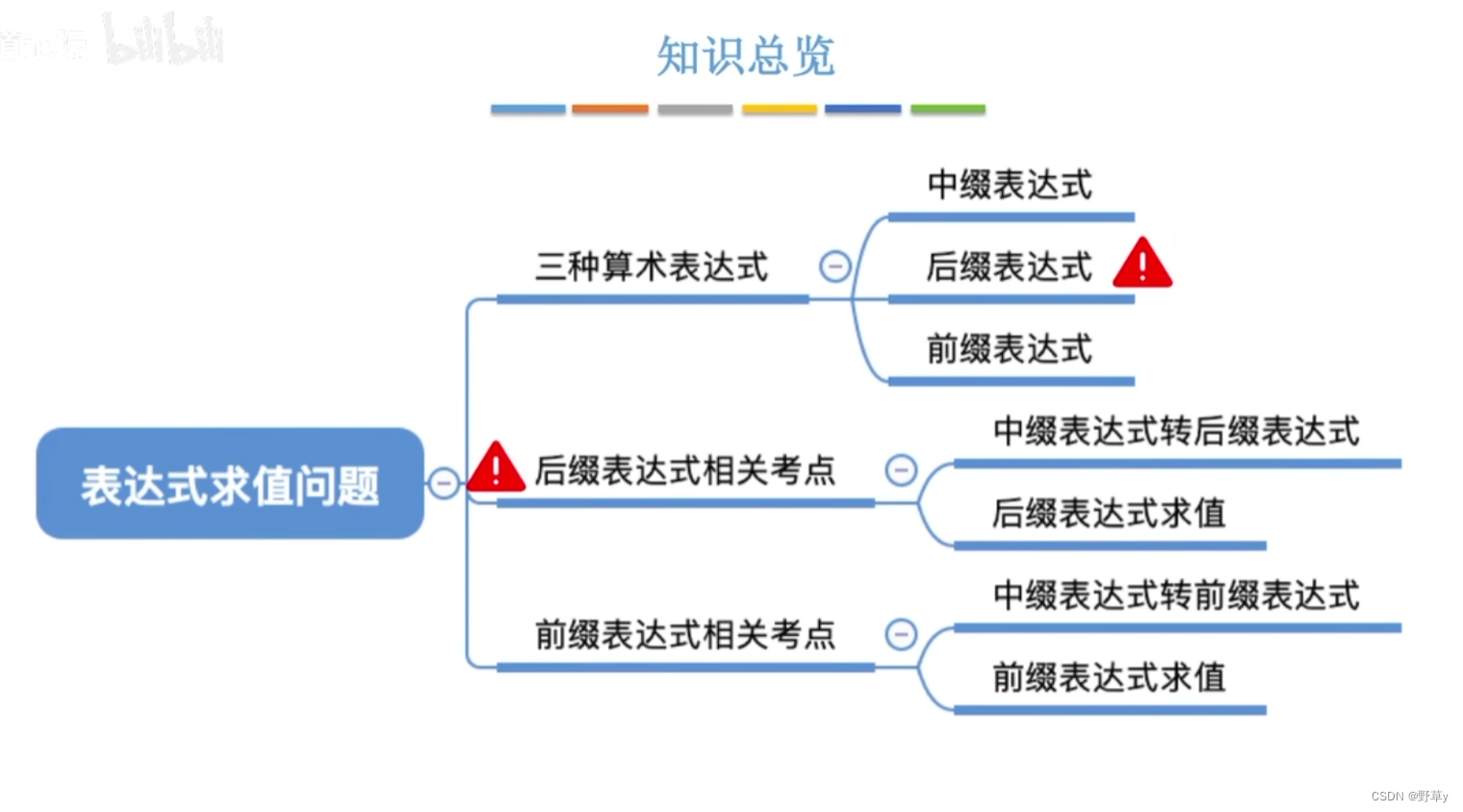
 中缀、后缀、前缀表达式
中缀、后缀、前缀表达式
中缀表达式
运算符在两个操作数中间:
- a + b
- a + b - c
- a + b - c * d
后缀表达式
运算符在两个操作数后面:
- ab +
- ab + c-或者a bc - +
- ab + cd * -
前缀表达式
运算符在两个操作数前面:
- + ab
- - + ab c
- - + ab * cd
中缀表达式转后缀表达式(手算)
- 确定中缀表达式中各个运算符的运算顺序
- 选择下一个运算符,按照[左操作数 右操作数 运算符]的方式组合成一个新的操作数(若运算顺序不唯一,则后缀表达式也不唯一)
- 如果还有运算符没被处理,就继续2步骤
例:
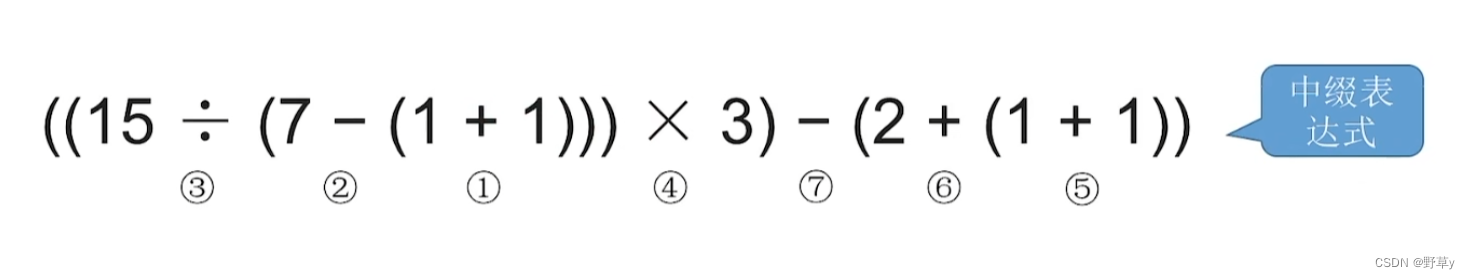 转换成后缀表式: 15 7 11+ - / 3 * 2 11 + + -
转换成后缀表式: 15 7 11+ - / 3 * 2 11 + + -
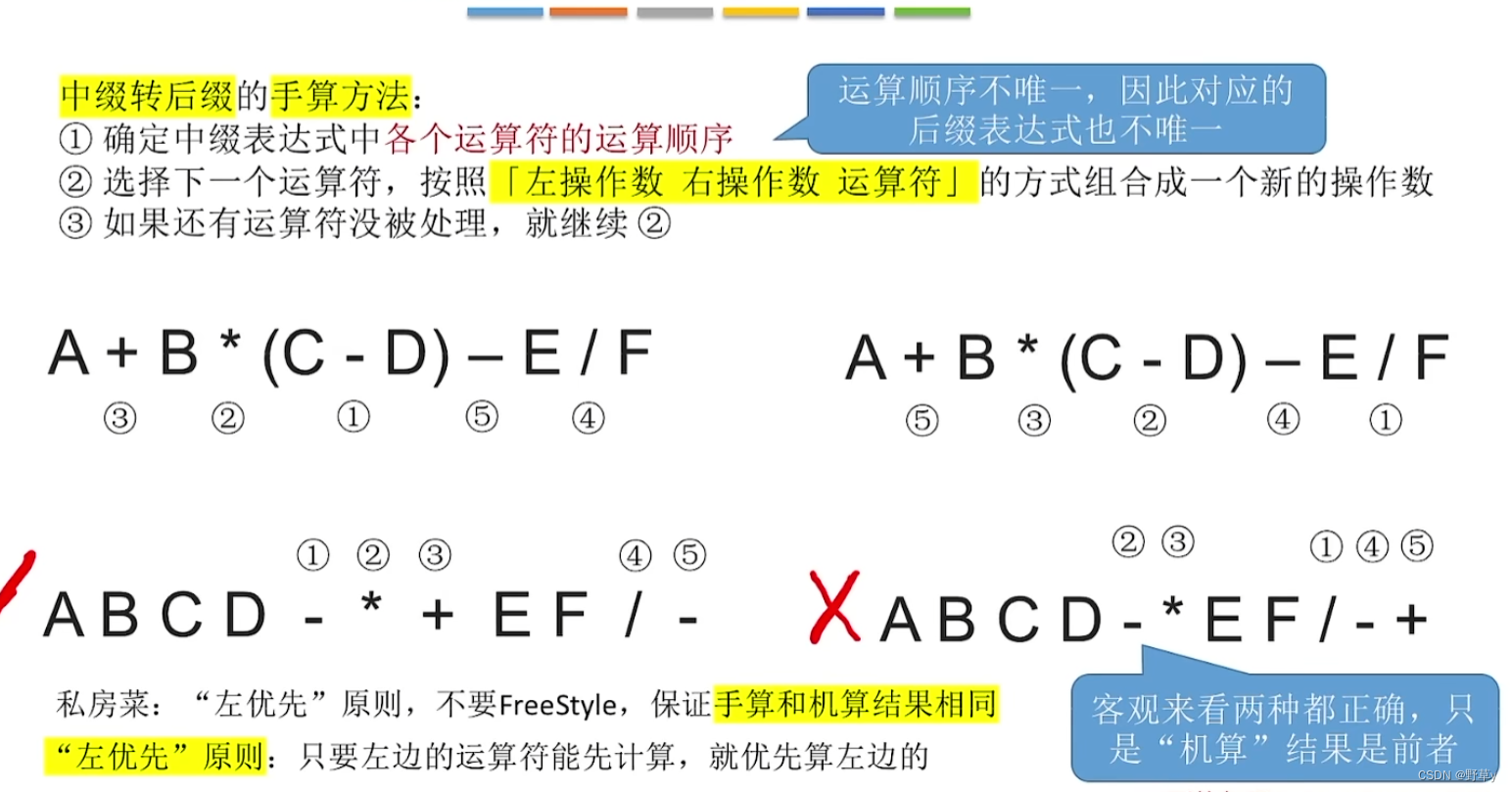

"左优先"原则:只要左边的运算符能先计算,就优先计算左边的(可保证运算唯一)
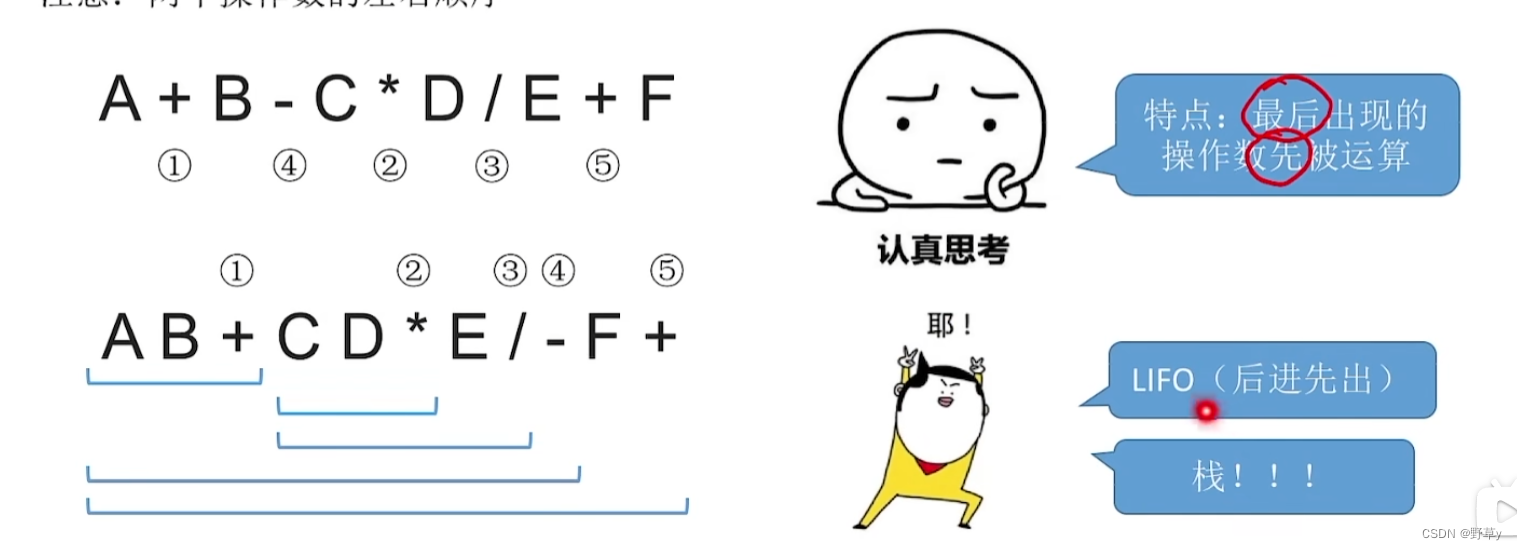
后缀表达式的计算(手算)
从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算,合体为一个操作数
注意:两个操作数的左右顺序

后缀表达式的计算(机算)
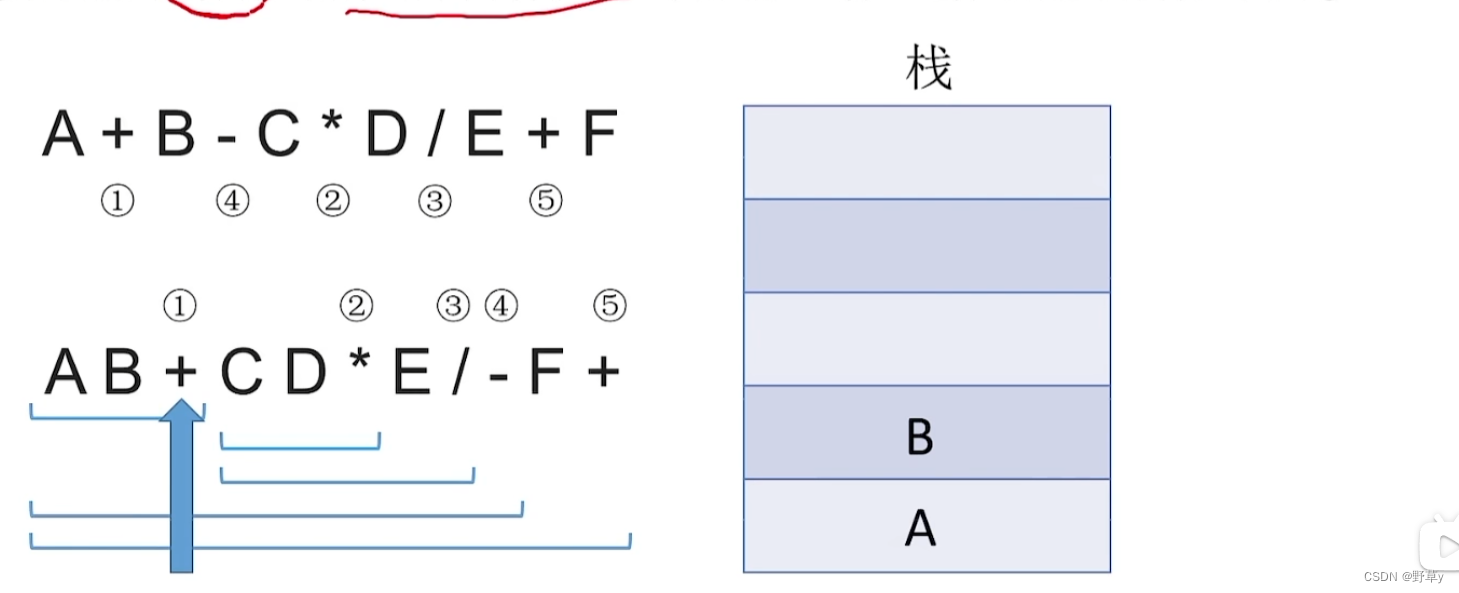
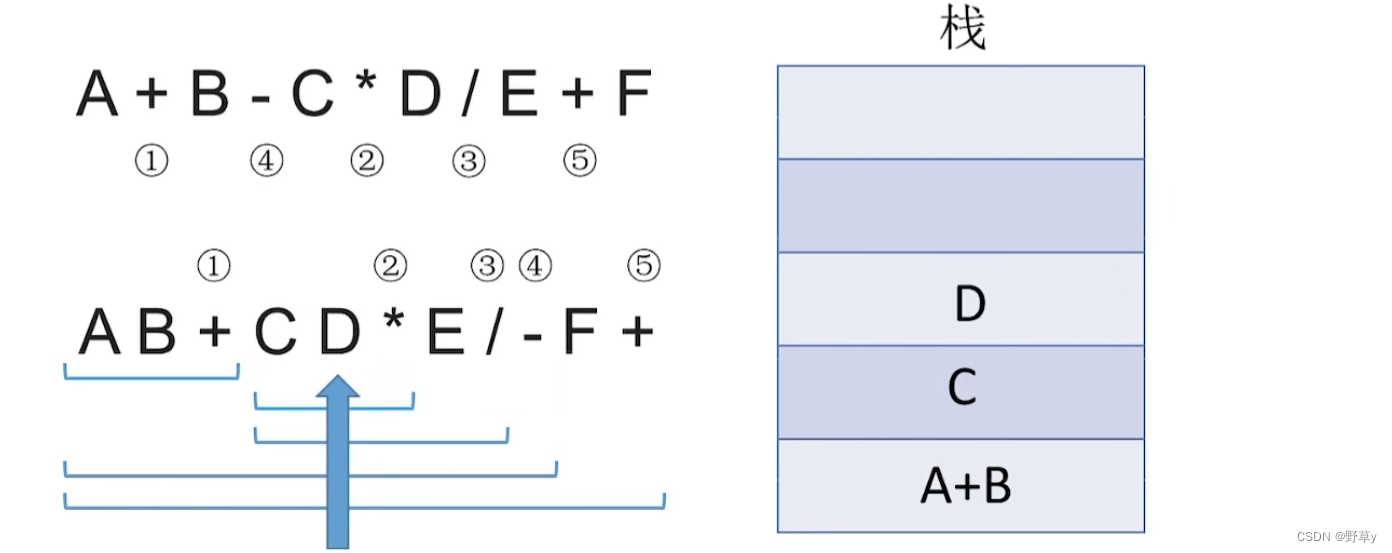
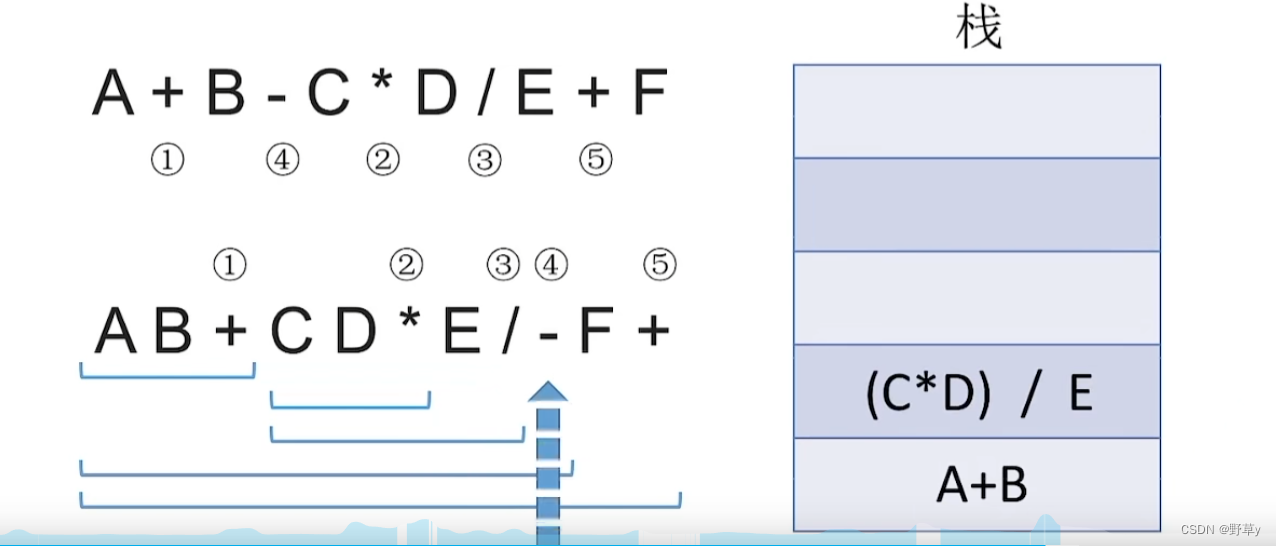
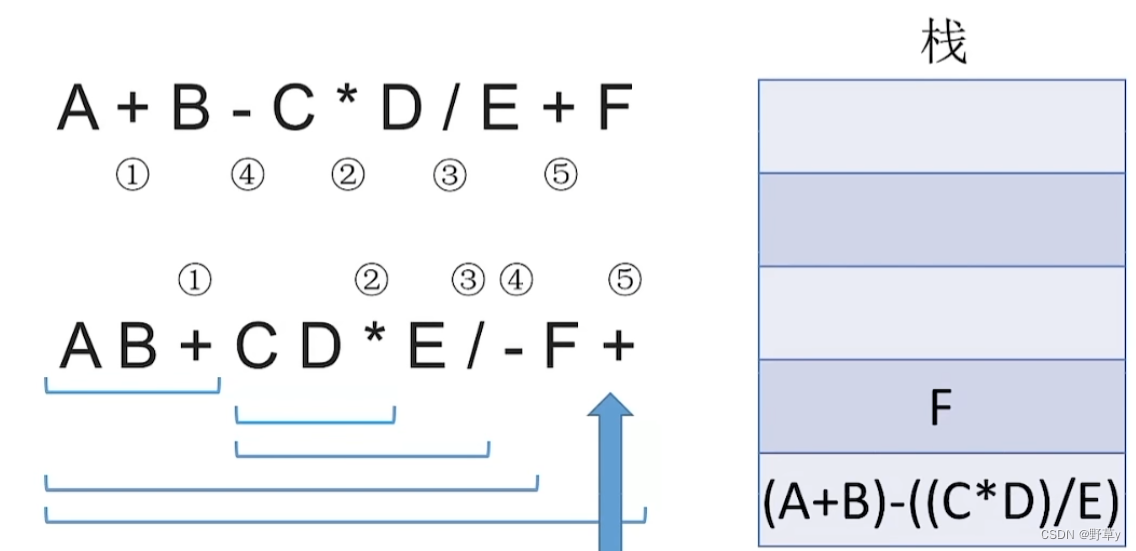
用栈实现后缀表达式的计算:
- 从左往右扫描下一个元素,直到处理完所以元素
- 若扫描到操作数则压入栈,并回到1;否则执行3
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到1
注意:后缀表达式先弹出的元素是‘右操作数’
入栈流程:


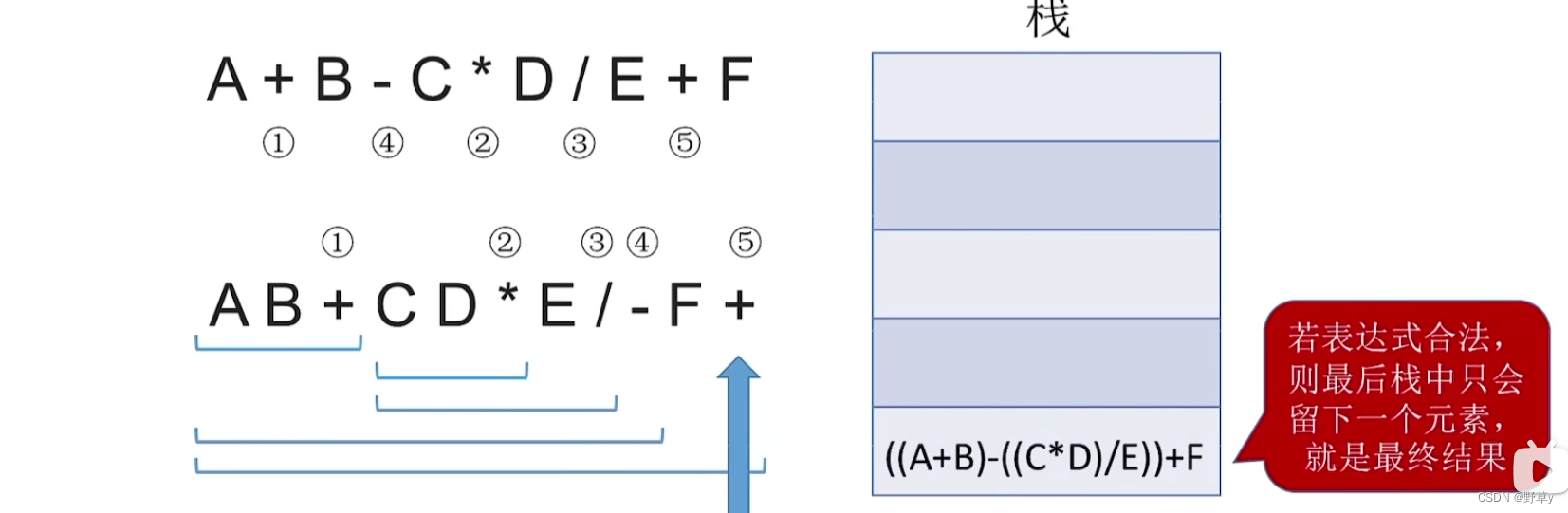
中缀表达式转前缀表达式(手算)
- 确定中缀表达式中各个运算符的运算顺序
- 确定下一个运算符,按照[运算符 左操作数 右操作数]的方式组合成一个新的操作数
- 如果还有运算符没被处理,就继续2
"右优先"原则:只要右边的运算符能先计算,就优先算右边的


前缀表达式的计算
- 从右往左扫描下一个元素,直到处理完所有元素
- 若扫描到操作数则压入栈,并回到1;否则执行3
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结构压回栈顶,回到1
注意前缀表达式先弹出的元素是‘左操作数’

总结