从零开始学习SLAM（三）

news2024/10/6 14:31:06

旋转向量

#include <Eigen/Geometry>
#include <Eigen/Core>

AngleAxisd 类有几种构造函数，其中最常用的是：

Eigen::AngleAxisd(const Scalar& angle, const Axis& axis);
  • angle 是旋转的角度，通常以弧度表示。
  • axis 是旋转的轴，通常是一个单位向量，表示旋转的方向。

例如，要创建一个围绕 Z 轴顺时针旋转 π/4 弧度（45度）的 AngleAxisd 对象，可以这样写：

Eigen::AngleAxisd rotation_angle_axis(M_PI / 4.0, Eigen::Vector3d::UnitZ());

或者是

Eigen::AngleAxisd rotation_angle_axis(M_PI / 4.0, Eigen::Vector3d(::UnitZ(0,0,1));

使用

使用 AngleAxisd 对象可以执行以下操作：

  • 将其应用于向量或点进行旋转：

    // 通过将 rotation_angle_axis 应用到 point 上得到的旋转后的新点
Eigen::Vector3d point(1.0, 0.0, 0.0);
Eigen::Vector3d rotated_point = rotation_angle_axis * point;

  • 转换为旋转矩阵或四元数：

    // 通过 toRotationMatrix() 方法从 rotation_angle_axis 转换而来，用于表示相同旋转的旋转矩阵
Eigen::Matrix3d rotation_matrix = rotation_angle_axis.toRotationMatrix();
// 通过直接将 rotation_angle_axis 赋值给 Eigen::Quaterniond 类型得到，也表示了同样旋转的四元数
Eigen::Quaterniond quaternion = rotation_angle_axis;

  • 进行组合和插值操作：

    // rotation_angle_axis 和 another_rotation 相乘（组合）得到的新的 Eigen::AngleAxisd 对象，它代表了先进行 rotation_angle_axis 的旋转，然后进行 another_rotation 的旋转。
Eigen::AngleAxisd another_rotation(M_PI / 3.0, Eigen::Vector3d::UnitY());
Eigen::AngleAxisd combined_rotation = rotation_angle_axis * another_rotation;
// interpolated_rotation 是通过 slerp() 方法进行球面线性插值（Slerp）得到的 Eigen::AngleAxisd 对象。这种方法可以在两个旋转之间进行平滑的过渡，第一个参数是插值参数，通常是一个介于0到1之间的值，表示两个旋转的相对比例。
Eigen::AngleAxisd interpolated_rotation = rotation_angle_axis.slerp(0.5, another_rotation);

欧氏变换

Eigen::Isometry3d 是 Eigen 库中用于表示三维欧氏空间中的等距变换（Isometry）的类。它继承自 Eigen::Transform，具体表示了包括平移和旋转在内的等距变换。

主要特点和用途：

  • Identity Isometry（单位等距变换）：单位等距变换表示没有任何旋转或平移，即一个点经过单位等距变换后位置不变。在三维空间中，单位等距变换的旋转部分是单位矩阵，平移部分是零向量。
  • 静态成员函数 Identity()：这个函数是通过 Isometry3d 类访问的静态函数，它返回一个默认的单位等距变换对象。通过调用 Eigen::Isometry3d::Identity()，可以获得一个已经初始化为单位变换的 Isometry3d 对象，通常用于开始定义其他具体的变换。
  1. 等距变换（Isometry）：Isometry3d 能够表示旋转和平移的组合，保持点之间的距离不变。在计算机图形学、机器人学和几何计算等领域中，等距变换非常重要。
  2. 旋转和平移的组合：通过 Isometry3d，可以方便地表示和操作三维空间中的物体的姿态和位置。
  3. Eigen 库支持：Eigen 是一个开源的线性代数库，专注于高性能的矩阵和向量运算。Isometry3d 类充分利用了 Eigen 的矩阵和向量运算优势，提供了高效的数学运算。

示例：

以下是一个简单的示例，展示如何使用 Isometry3d 类创建和操作等距变换：

#include <Eigen/Geometry>

int main() {
    // 创建一个 Isometry3d 对象
    Eigen::Isometry3d T = Eigen::Isometry3d::Identity();

    // 设置旋转部分（绕Z轴旋转90度）
    T.rotate(Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d::UnitZ()));

    // 设置平移部分（平移向量）
    T.pretranslate(Eigen::Vector3d(1, 2, 3));

    // 使用 Isometry3d 进行点变换
    Eigen::Vector3d point(1, 0, 0);
    Eigen::Vector3d transformed_point = T * point;

    // 输出变换后的点
    std::cout << "Transformed point: " << transformed_point.transpose() << std::endl;

    return 0;
}

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 假设我们有一个4x4的仿射变换矩阵
    Eigen::Affine3d T;
    T.matrix() << 
        1, 0, 0, 1, // 旋转矩阵部分
        0, 1, 0, 0, // 旋转矩阵部分
        0, 0, 1, 0, // 旋转矩阵部分
        1, 2, 3, 1; // 平移向量

    // 提取旋转矩阵
    Eigen::Matrix3d R = T.linear();
    
    // 提取平移向量
    Eigen::Vector3d t = T.translation();
    
    // 打印旋转矩阵和平移向量
    std::cout << "Rotation matrix:\n" << R << std::endl;
    std::cout << "Translation vector:\n" << t.transpose() << std::endl;
    
    return 0;

}

T.linear()

这个成员函数返回仿射变换中的线性部分，即旋转矩阵。它返回的是一个Eigen::Matrix3d类型的引用，代表3x3的旋转矩阵。

T.translation()

这个成员函数返回仿射变换中的平移向量。它返回的是一个Eigen::Vector3d类型的引用，代表3D空间中的平移。

T.rotate()

这个成员函数是用来设置仿射变换的旋转部分的。你可以传递一个3x3的旋转矩阵给这个函数，它会更新T的线性部分。

旋转矩阵

Eigen::Matrix3d 在实际应用中有许多用途，以下是几个常见的例子：

1. 旋转矩阵表示旋转操作

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 定义一个旋转矩阵，将向量绕Z轴旋转45度
    Eigen::Matrix3d rotation_matrix;
    double angle = M_PI / 4.0; // 45度
    rotation_matrix << cos(angle), -sin(angle), 0,
                       sin(angle), cos(angle), 0,
                       0, 0, 1;

    // 定义一个向量
    Eigen::Vector3d vector(1.0, 0.0, 0.0);

    // 将向量应用旋转
    Eigen::Vector3d rotated_vector = rotation_matrix * vector;

    // 输出结果
    std::cout << "Original vector: " << vector.transpose() << std::endl;
    std::cout << "Rotated vector: " << rotated_vector.transpose() << std::endl;

    return 0;
}

这个例子中，我们定义了一个 Eigen::Matrix3d 类型的 rotation_matrix，表示绕Z轴旋转45度的旋转矩阵。然后，我们定义了一个 Eigen::Vector3d 类型的向量 vector，并将其通过 rotation_matrix 进行旋转操作，得到 rotated_vector。最后输出了旋转前后的向量。

2. 坐标变换

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 定义一个坐标变换矩阵，将点从局部坐标系变换到全局坐标系
    Eigen::Matrix3d coordinate_transform;
    coordinate_transform << 1, 0, 0,
                            0, -1, 0,
                            0, 0, 1;

    // 定义一个局部坐标系下的点
    Eigen::Vector3d local_point(2.0, 3.0, 1.0);

    // 应用坐标变换
    Eigen::Vector3d global_point = coordinate_transform * local_point;

    // 输出结果
    std::cout << "Local point: " << local_point.transpose() << std::endl;
    std::cout << "Global point: " << global_point.transpose() << std::endl;

    return 0;
}

在这个例子中，我们定义了一个 Eigen::Matrix3d 类型的 coordinate_transform，表示一个坐标系的变换矩阵，用来将局部坐标系下的点 local_point 转换到全局坐标系下的 global_point。这种方式在计算机图形学和仿真中经常使用，用于物体的位置和姿态变换。

3. 矩阵运算

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 定义两个矩阵
    Eigen::Matrix3d A, B;
    A << 1, 2, 3,
         4, 5, 6,
         7, 8, 9;
    B << 9, 8, 7,
         6, 5, 4,
         3, 2, 1;

    // 计算矩阵乘法
    Eigen::Matrix3d result = A * B;

    // 输出结果
    std::cout << "Matrix A:\n" << A << std::endl;
    std::cout << "Matrix B:\n" << B << std::endl;
    std::cout << "Result of A * B:\n" << result << std::endl;

    return 0;
}

当使用Eigen库进行旋转表示的转换时，可以如下操作：

1. 旋转矩阵转换为旋转向量

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 定义一个旋转矩阵，例如绕Y轴旋转30度
    Eigen::Matrix3d rotation_matrix;
    double angle = M_PI / 6.0; // 30度
    rotation_matrix << cos(angle), 0, sin(angle),
                       0, 1, 0,
                       -sin(angle), 0, cos(angle);

    // 将旋转矩阵转换为旋转向量
    Eigen::AngleAxisd rotation_vector(rotation_matrix);

    // 输出结果
    std::cout << "Rotation matrix:\n" << rotation_matrix << std::endl;
    std::cout << "Equivalent rotation vector:\n" << rotation_vector.axis().transpose()
              << " " << rotation_vector.angle() << " radians" << std::endl;

    return 0;
}

在这个例子中，我们定义了一个旋转矩阵 rotation_matrix，表示绕Y轴旋转30度。然后，使用 Eigen::AngleAxisd 类型的构造函数将旋转矩阵转换为对应的旋转向量 rotation_vector。通过 rotation_vector.axis() 获取旋转向量的轴向量，通过 rotation_vector.angle() 获取旋转角度。

2. 旋转矩阵转换为四元数

Eigen::Matrix3d rotation_matrix;
// 填充旋转矩阵

Eigen::Quaterniond quaternion(rotation_matrix);

这段代码示例已经在前面提供过，展示了如何将旋转矩阵 rotation_matrix 转换为对应的四元数 quaternion。

3. 旋转矩阵转换为欧拉角

Eigen库中没有直接提供将旋转矩阵转换为欧拉角的函数，但可以通过以下步骤手动实现欧拉角的计算：

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 定义一个旋转矩阵，例如绕Z轴旋转60度
    Eigen::Matrix3d rotation_matrix;
    double angle = M_PI / 3.0; // 60度
    rotation_matrix << cos(angle), -sin(angle), 0,
                       sin(angle), cos(angle), 0,
                       0, 0, 1;

    // 计算欧拉角（ZYX顺序）
    double phi = atan2(rotation_matrix(1, 0), rotation_matrix(0, 0));
    double theta = atan2(-rotation_matrix(2, 0), sqrt(rotation_matrix(2, 1) * rotation_matrix(2, 1) + rotation_matrix(2, 2) * rotation_matrix(2, 2)));
    double psi = atan2(rotation_matrix(2, 1), rotation_matrix(2, 2));

    // 输出结果
    std::cout << "Rotation matrix:\n" << rotation_matrix << std::endl;
    std::cout << "Equivalent Euler angles (ZYX order):\n"
              << "Phi (roll): " << phi << " radians\n"
              << "Theta (pitch): " << theta << " radians\n"
              << "Psi (yaw): " << psi << " radians" << std::endl;

    return 0;
}

在这个例子中，我们定义了一个旋转矩阵 rotation_matrix，表示绕Z轴旋转60度。然后，通过手动计算欧拉角（ZYX顺序），即 roll (phi), pitch (theta), yaw (psi)，从旋转矩阵中提取这些角度信息。

这些例子展示了如何使用 Eigen 库进行旋转表示的各种转换，从而在不同的场景中方便地处理旋转操作。

四元数

Eigen::Quateriond

Eigen::Quaterniond 是 Eigen 库中用于表示双精度（double）的四元数的类。四元数在计算机图形学和机器人学等领域中广泛用于表示旋转。让我展示如何使用 Eigen::Quaterniond 类来创建和操作四元数：

创建一个四元数

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 创建一个四元数，表示绕Z轴旋转45度
    Eigen::Quaterniond quaternion;
    double angle = M_PI / 4.0; // 45度
    quaternion = Eigen::Quaterniond(cos(angle / 2), 0, 0, sin(angle / 2));

    // 输出四元数的信息
    std::cout << "Quaternion:\n" << quaternion.coeffs().transpose() << std::endl;

    return 0;
}

在这个例子中，我们创建了一个四元数 quaternion，它表示绕Z轴旋转45度。四元数的构造方法 Eigen::Quaterniond 接受四个参数 (w, x, y, z)，分别表示四元数的实部和虚部（三个虚部分量）。在这里，我们使用角度 angle 计算实部 w 和虚部 z。

操作四元数

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 创建一个四元数，表示绕Z轴旋转45度
    Eigen::Quaterniond quaternion(cos(M_PI / 8), 0, 0, sin(M_PI / 8));

    // 获取旋转矩阵
    Eigen::Matrix3d rotation_matrix = quaternion.toRotationMatrix();

    // 输出旋转矩阵
    std::cout << "Rotation matrix:\n" << rotation_matrix << std::endl;

    return 0;
}

#include <Eigen/Dense>
#include <iostream>

int main() {
    // 创建一个四元数，表示绕Z轴旋转45度
    Eigen::Quaterniond quaternion(cos(M_PI / 8), 0, 0, sin(M_PI / 8));

    // 获取旋转矩阵
    Eigen::Matrix3d rotation_matrix = quaternion.toRotationMatrix();

    // 输出旋转矩阵
    std::cout << "Rotation matrix:\n" << rotation_matrix << std::endl;

    return 0;
}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1895319.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何在 Odoo 16 中添加计算字段的搜索过滤器

如何在 Odoo 16 中添加计算字段的搜索过滤器

首先&#xff0c;了解 Odoo 使用计算字段的原因很重要。当我们需要从其他字段获取计算值或计算值时&#xff0c;就会使用计算字段。换句话说&#xff0c;不是从数据库中检索值&#xff0c;而是可以使用函数计算字段的值。计算字段的一个例子是产品总金额&#xff0c;即通过将产…
阅读更多...
阶段三：项目开发---大数据系统基础环境准备：任务1：准备系统运行的先决条件

阶段三：项目开发---大数据系统基础环境准备：任务1：准备系统运行的先决条件

任务描述 知识点&#xff1a; 大数据基础环境准备 重 点&#xff1a; SSH免密码连接 安装配置JDK 安装配置Scala 难 点&#xff1a; 无 内 容&#xff1a; 项目开发测试环境为分布式集群环境&#xff0c;在当前项目中使用多台基于CentOS 64bit 的虚拟机来模拟生产…
阅读更多...
SpringBoot应用配置桥接Prometheus入门

SpringBoot应用配置桥接Prometheus入门

SpringBoot应用配置Prometheus步骤 SpringBoot应用依赖要求PrometheusGrafanaGrafana监控界面模板 SpringBoot应用依赖要求 <!-- 监控系统健康情况的工具 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot…
阅读更多...
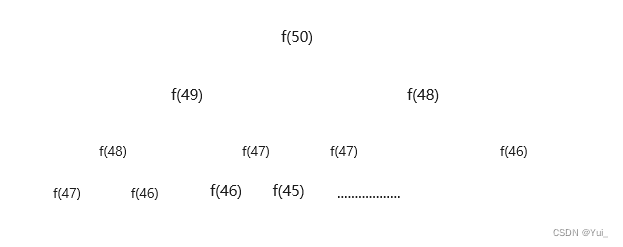
完全理解C语言函数

完全理解C语言函数

文章目录 1.函数是什么2.C语言中的函数分类2.1 库函数2.1.1 如何使用库函数 2.2自定义函数 3.函数的参数3.1 实际参数&#xff08;实参&#xff09;3.2 形式参数&#xff08;形参&#xff09; 4.函数调用4.1传值调用4.2 传址调用4.3 练习 5.函数的嵌套调用和链式访问5.1 嵌套调…
阅读更多...
echarts柱状选中shadow阴影背景宽度设置

echarts柱状选中shadow阴影背景宽度设置

使用line&#xff0c;宽度增大到所需要的宽度&#xff0c;设置下颜色透明度就行 tooltip: {trigger: axis,//把阴影的层级往下降z:-15,axisPointer: {type: line,lineStyle: {color: rgba(150,150,150,0.3),width: 44,type: solid,},}, }, series: [{type: bar,barWidth:20,//…
阅读更多...
Jemeter--关联接口压测

Jemeter--关联接口压测

Jemeter–独立不变参接口压测 Jemeter–独立变参接口压测 Jemeter–关联接口压测 案例分析 比如&#xff1a;有个波次复核接口很慢&#xff0c;优化后需要压测。但是波次复核接口数据是由另外两个接口&#xff08;配单详情、内盒信息&#xff09;的数据组合而来&#xff0c;而…
阅读更多...
人脸重建迁移攻击FRTA：绕过各种未见过的面部识别系统

人脸重建迁移攻击FRTA：绕过各种未见过的面部识别系统

随着人脸识别系统在安全关键环境中的部署日益增多&#xff0c;威胁行为者正在开发针对各种攻击点的复杂攻击策略。在这些攻击策略中&#xff0c;面部重建攻击是一个主要的威胁。面部重建攻击的主要目的是创建伪造的生物特征图像&#xff0c;这些图像类似于存储的生物特征模板中…
阅读更多...
更改Anki笔记所应用的模板及其所属的牌组

更改Anki笔记所应用的模板及其所属的牌组

对于Anki中的笔记&#xff0c;录入时总会为它指定模板以及所属的牌组&#xff0c;但是&#xff0c;如果发生教材版本变更&#xff0c;我们可能会用新的模板添加笔记&#xff0c;也会使用新的牌组&#xff0c;但是原来所做的笔记中也有一些完全可以继续使用&#xff0c;如果可以…
阅读更多...
Java 应用启动时出现编译错误进程会退出吗？

Java 应用启动时出现编译错误进程会退出吗？

背景 开发的尽头是啥呢&#xff1f;超超级熟练工&#xff01; 总结最近遇到的一些简单问题&#xff1a; Java 应用的某个线程&#xff0c;如果运行时依赖的 jar 不满足&#xff0c;线程是否会退出&#xff1f;进程是否会退出&#xff1f;Netty 实现 TCP 功能时&#xff0c;换…
阅读更多...
Django创建项目(1)

Django创建项目(1)

运行 注意 在本次创建Django项目时&#xff0c;出现了一点小问题&#xff0c;由于我之前pip换源过&#xff0c;换源用的是http&#xff0c;结果在创建时&#xff0c;pip只支持https&#xff0c;所以如果出现创建项目失败的问题&#xff0c;那么有可能是因为换源的问题&#xf…
阅读更多...
C++左值/右值/左值引用/右值引用

C++左值/右值/左值引用/右值引用

1&#xff09;C入门级小知识&#xff0c;分享给将要学习或者正在学习C开发的同学。 2&#xff09;内容属于原创&#xff0c;若转载&#xff0c;请说明出处。 3&#xff09;提供相关问题有偿答疑和支持。 左值和右值的概念&#xff1a; 早期的c语言中关于左值和右值的定义&a…
阅读更多...
基于轨迹信息的图像近距离可行驶区域方案验证

基于轨迹信息的图像近距离可行驶区域方案验证

一 图像可行驶区域方案 1.1 标定场景 1.2 标定步骤 设计一定间距标定场&#xff0c;在标定场固定位置设置摄像头标定标识点。主车开到标定场固定位置录制主车在该位置各个摄像头数据&#xff0c;通过摄像头捕获图像获取图像上关键点坐标pts-2d基于标定场设计&#xff0c;计算…
阅读更多...
Windows上使用Navicat连接ubuntu上的mysql8报错:10061和1130

Windows上使用Navicat连接ubuntu上的mysql8报错:10061和1130

问题一&#xff1a;can’t connect to mysql server on ‘192.168.xxx.xxx’(10061) 解决&#xff1a; sudo vim /etc/mysql/mysql.conf.d/mysqld.cnf&#xff0c;bind-address绑定了登陆的IP&#xff0c;把这两行代码注释掉&#xff0c;然后重启mysql。 问题二&#xff1a;1…
阅读更多...
WMS系统对小型海外仓有哪些好处？规模不大有必要用吗？

WMS系统对小型海外仓有哪些好处？规模不大有必要用吗？

作为一家想持续发展的海外仓&#xff0c;虽然目前的规模还不大&#xff0c;但是也需要不断优化仓库的作业效率。实施海外仓WMS系统是个不错的选择。 海外仓WMS系统的实施&#xff0c;不仅可以提升库存管理水平和一件代发等核心业务的效率&#xff0c;还能提升工人的生产效率&a…
阅读更多...
智能本质：马毅教授对大模型和白盒理论的观点

智能本质：马毅教授对大模型和白盒理论的观点

引言 在人工智能的快速发展中&#xff0c;我们见证了从简单的自动化工具到复杂的智能系统的演变。随着深度学习技术的突破&#xff0c;大模型如GPT系列已经能够执行从文本生成到图像识别等多样化任务。然而&#xff0c;这些模型虽然在功能上取得了显著进展&#xff0c;但其内部…
阅读更多...
洛谷 P1011 [NOIP1998 提高组] 车站

洛谷 P1011 [NOIP1998 提高组] 车站

题目描述 火车从始发站&#xff08;称为第 1 站&#xff09;开出&#xff0c;在始发站上车的人数为 a&#xff0c;然后到达第 2 站&#xff0c;在第 2 站有人上、下车&#xff0c;但上、下车的人数相同&#xff0c;因此在第 2 站开出时&#xff08;即在到达第 3 站之前&#x…
阅读更多...
存储器类型介绍

存储器类型介绍

存储器 ROM 我们一般把手机和电脑的硬盘当作ROM。ROM的全称是&#xff1a;Read Only Memery&#xff0c;只读存储器&#xff0c;就是只能读不能写的存储器。但是现在的ROM不仅可以读&#xff0c;还可以写数据&#xff0c;比如给手机下载APP&#xff0c;就是给手机上的ROM写数据…
阅读更多...
闲鱼商品搜索关键词优化攻略

闲鱼商品搜索关键词优化攻略

一、闲鱼商品详情关键词搜索概述 闲鱼作为国内最大的二手交易平台之一&#xff0c;其商品搜索功能对于买家和卖家来说至关重要。商品详情页中的关键词搜索功能&#xff0c;可以帮助买家更快速地找到心仪的商品&#xff0c;也可以帮助卖家提高商品的曝光度&#xff0c;从而促进…
阅读更多...
半导体制造企业 文件共享存储应用

半导体制造企业 文件共享存储应用

用户背景&#xff1a;半导体设备&#xff08;上海&#xff09;股份有限公司是一家以中国为基地、面向全球的微观加工高端设备公司&#xff0c;为集成电路和泛半导体行业提供具竞争力的高端设备和高质量的服务。 挑战&#xff1a;芯片的行业在国内迅猛发展&#xff0c;用户在上海…
阅读更多...
版本控制系统：Git 纯应用（持续更新）；

版本控制系统：Git 纯应用（持续更新）；

基本操作 ctrl上行键&#xff1a;上次代码 本地仓库&#xff1a;Git init 新建文件&#xff1a;touch xxxx.xxx 查看状态&#xff1a;Git status 文件从工作区——暂存区&#xff1a;Git add ./文件名(.是通配符代表所有) 暂存区——仓库&#xff1a;Git commit -m &…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023