什么是激活函数

计算机科学家借鉴生物的神经元机制发明了计算机上的模型，这个模型与生物的神经元非常类似

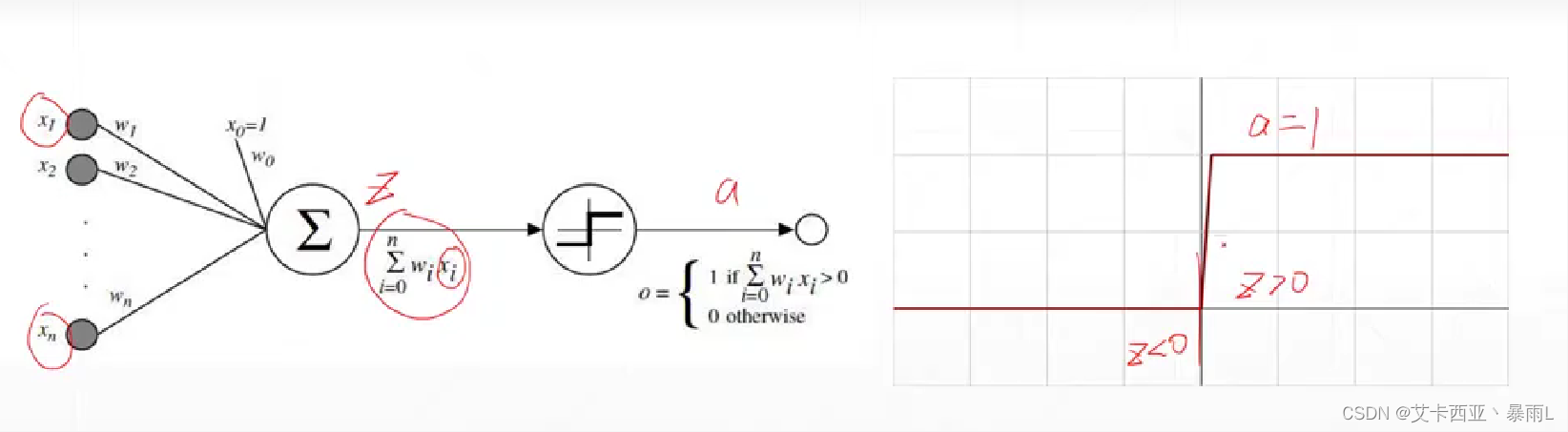
激活的意思就是z变量要大于0，这一个节点才会激活，否则就会处于睡眠状态不会输出电平值

该激活函数在z=0处不可导，因此不能直接使用梯度下降进行优化，使用了启发式搜索的方法来求解单层感知机最优解的情况

sigmoid

为了解决单层感知机激活函数不可导的情况，提出了一个连续的光滑的函数即sigmoid函数或者叫logistic

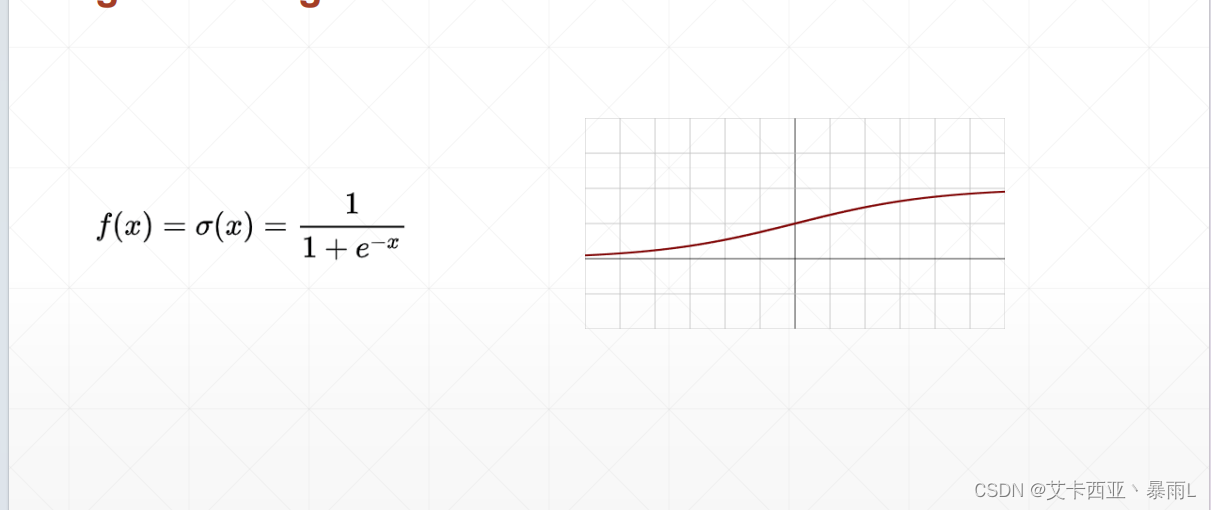
sigmoid函数z=0的时候值为0.5，最大值是接近于1，最小值是接近于0

比较适合生物学上的神经元，也就是说当z比较小的时候，接近于一个不响应的状态，z很大的时候我这个响应也不会很大会慢慢接近于1，相当于一个压缩的功能，把(-∞，+∞)Z的这样的值压缩到一个有限的范围中间，比如(0,1)

该函数的导数在负无穷的时候接近于0，到z=0的时候会出现最大值，再慢慢导数再变成0

有一个缺陷：loss长时间保持不变，梯度弥散

torch.sigmoid和F.sigmoid是一样的
F是一个模块的别名，是torch.nn.functional

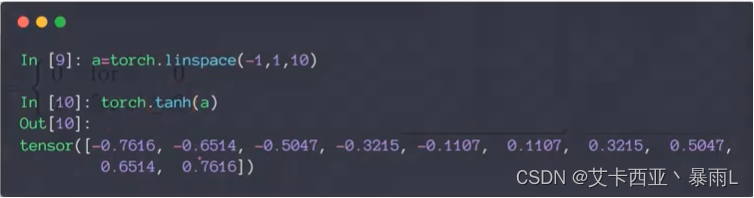
z的值接近于-100的时候，sigmoid的值已经接近于0了，取100的时候，sigmoid接近于1

Tanh

在RNN（循环神经网络）中使用较多

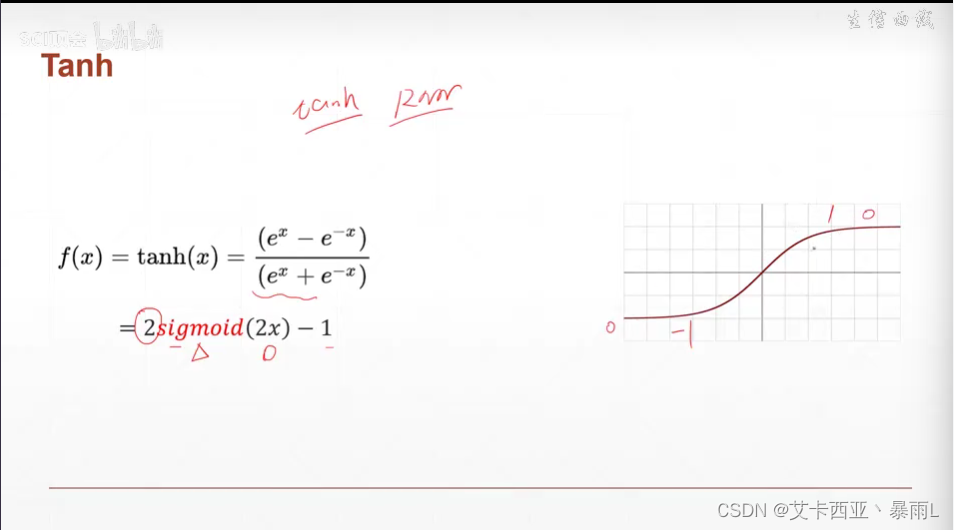
可以由sigmoid变化而来，将x压缩二分之一，y放大两倍，再减去1

区间从(-1,1)

ReLu

z小于0不响应，z大于0就线性响应，非常合适做深度学习

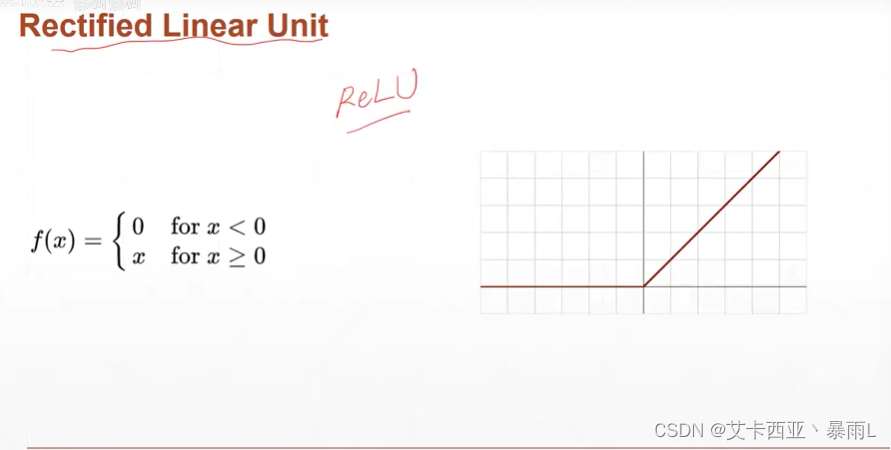
当z<0，梯度是0；z>0的时候，梯度是1，因为梯度是1，可以导致梯度计算起来非常方便，不会放大也不会缩小，因此对于搜索最优解，relu函数存在优势，不会出现梯度弥散和梯度爆炸的情况

loss以及loss的梯度

• Mean Squared Error （均方差）
• Cross Entropy Loss（用于分类中的误差）
  • binary（二分类）
  • multi-class（多分类）
  • +softmax（一般跟softmax激活函数一起使用）
  • leave it to logistic regression part

MSE

MSE的基本形式就是y的实际值减去模型输出的值

MSE与L2-norm是有一定区别的，对于第一个tensor y1和第二个tensor xw+b 设其为y2，l2 norm是对应元素相减再开根号，如下

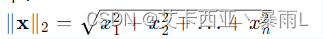
所以跟MSE还是有区别的,MSE是没有开根号这个步骤的

如果要用norm函数来求解MSE，需求平方，比如说
torch.norm(y-pred,2).pow(2)第二个参数是给出 L几-norm，一定要加一个pow(2)

MSE梯度求解情况

使用pytorch自动求导

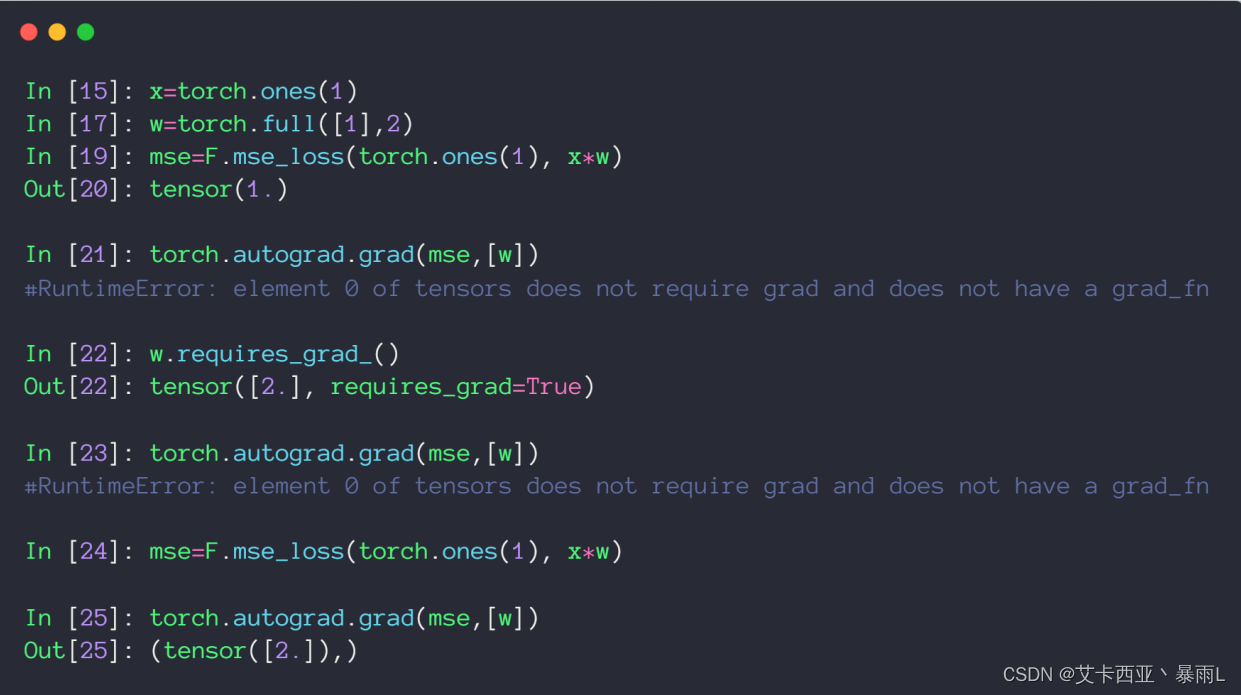
x初始化为1 w初始化为dimension为1，长度为1，值为2的tensor，b为0

求解MSE可以使用torch.norm加平方，也可以使用F.mse_loss第一个参数给的是predict的值，第二个参数给的是真实值，因为是平方所以这里顺序乱了也没有关系

使用torch.autograd.grad接收两个参数，第一个参数是y，第二个参数是[x1,x2,…]（即有多少个自变量，要对多少个自变量求导），对于深度学习来说，第一个参数就是predict，第二个参数是[w1,w2,…]这种参数

直接使用MSE也就是输出的这个loss对W求导的时候，上图返回该参数不需要求导的ERROR，出现该错误的根本原因是w初始化的时候没有设置为需要导出信息，因此pytorch在建图的时候对w标注了不需要求导信息，这样对w求导就会触发错误
需要使用requires_grad进行更新，但是更新完之后还是会报错，因为pytorch是一个动态图，这里更新了w但是图还没有更新，pytorch是做一步计算，一步图，所以w更新之后，图还是用的原来的图，所以还是会出现原来的错误

使用另一种方法

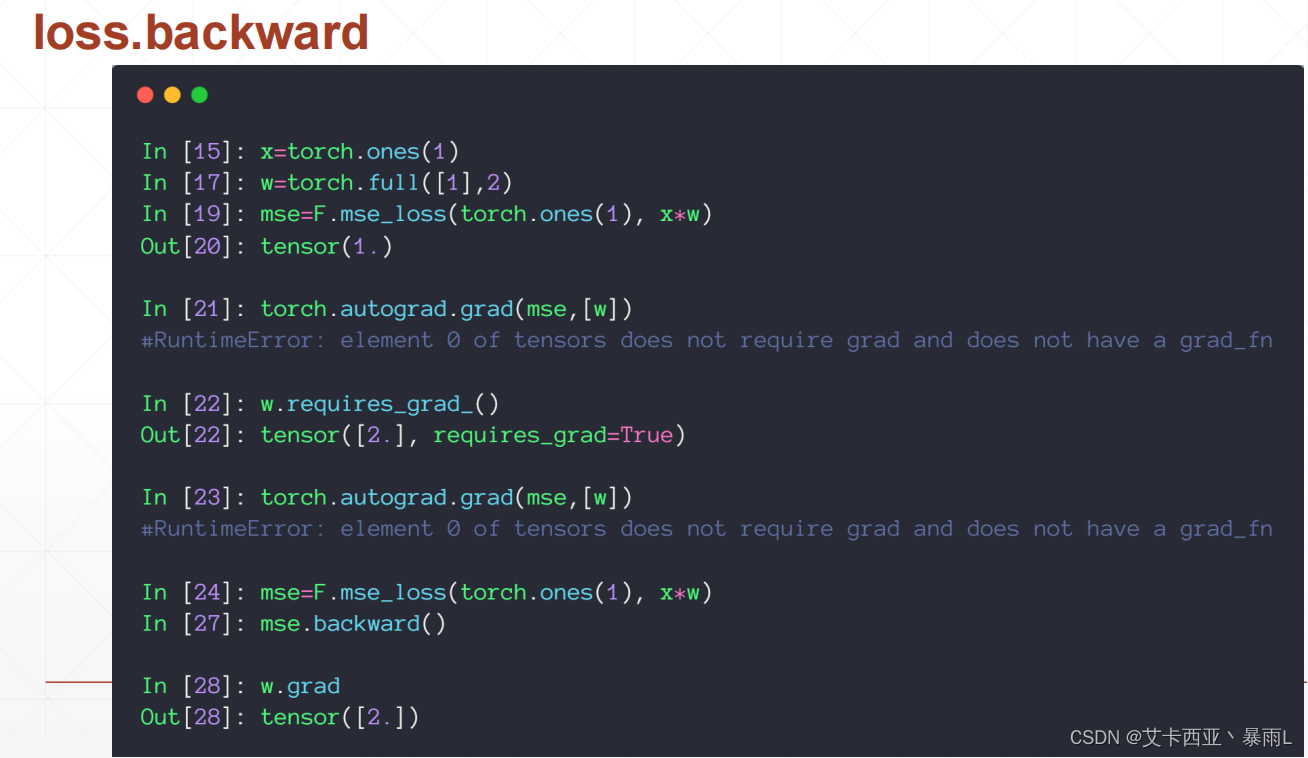
首先也是要用F.mse_loss动态图建图,直接在loss上使用backward（表示向后传播），自动对这个图（在完成前向传播的时候建图的过程中会记录下来这个图的所有路径，因此在最后的loss节点调用backward的时候，会自动的从后往前传播，完成路径上所有需要梯度的tensor的gradient的计算方法，计算的gradient不会再返回出来，会自动把所有的gradient信息附加在每个tensor的成员变量上面）

softmax

首先对于三个节点的输出，如果把这个数值转换成一个概率的话，希望概率最大的那个值做预测的Label，比如这里输入的索引是0，1，2，我们希望数值最大的值所在的索引作为我们预测的label，因此2.0最大，把2.0所在的索引0作为我们预测的一个label，因为probability是属于一个区间的（0~1这样的范围），我们需要把这个值转换成一个probability的话必须人为的压缩到这样的一个空间，可以使用sigmoid函数把值压缩到0 ~ 1的区间，但是对于一个分类问题来说一个物体属于哪个类是有一个概率的属性的（即物体属于x分类的概率，y分类的概率，z分类的概率等）总是属于着三个分类中的一种，因此这三个分类加起来总是会等于1，即sigmoid并不能表述所有输出节点的概率相加为1的情况，会把原来大的放大，原来小的压缩到密集的空间

$a_i$经过softmax得到$p_i$，$p_i$对$a_j$求导，假设i=j时如右图所示，softmax的梯度等于

之所以要利用$p_j$的输出是因为神经网络向前传播的时候，这些值是已知的可以直接得到，因此向后传播的时候不需要额外计算，只需要利用这个公式就可以一次求出

当i不等于j的时候

i不等于j的时候

总结

i=j时偏导时正数，不相等时是负数

loss必须只有一个量[1]，否则就会有逻辑错误，这里p.shape为[3]，因此在求梯度的时候不能直接传入p，只能对中的变量进行求导，此时图中是$p_1$对$a_i$ i属于[0,2]，所以会返回dimension为1 长度为3 的tensor，其中第一个元素表示$p_1$对$a_0$求偏导以此类推，可以看出如果i等于j的话梯度信息就是正的，其他的都是负的