---

---

图

图的知识盘点

pathfinding

作为一名计算机专业的学生，对于图这种数据结构也是烂熟于心了。图是一种包含了多个结点的数据结构，它是结点和路径的集合。可以用邻接表和邻接矩阵来表示一张图。

图的表示可以通过计算得到结点之间的可达和不可达，耗费的代价等等。在许多数学问题上十分有用。通常解决图问题的算法被我们称为寻路算法。

寻路算法

在大学期间，我们就学习过一些基本的寻路算法：

BFS广度优先算法

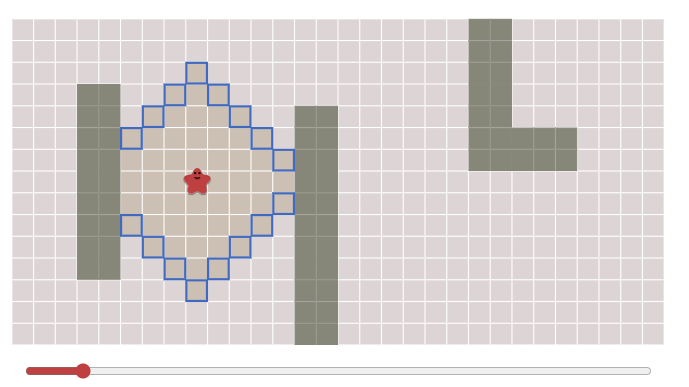
广度优先算法的原理是，以起始点为中心，向四周的相邻点（也就是与当前点连通且路长为1的那些节点）依次遍历。当遍历完相邻节点后，再遍历相邻结点的相邻点，依次类推。

当找到结束点后，只需要从终点开始，反向按着相邻节点的最小遍历序号数寻找，就能找到最短路径了

DFS深度优先

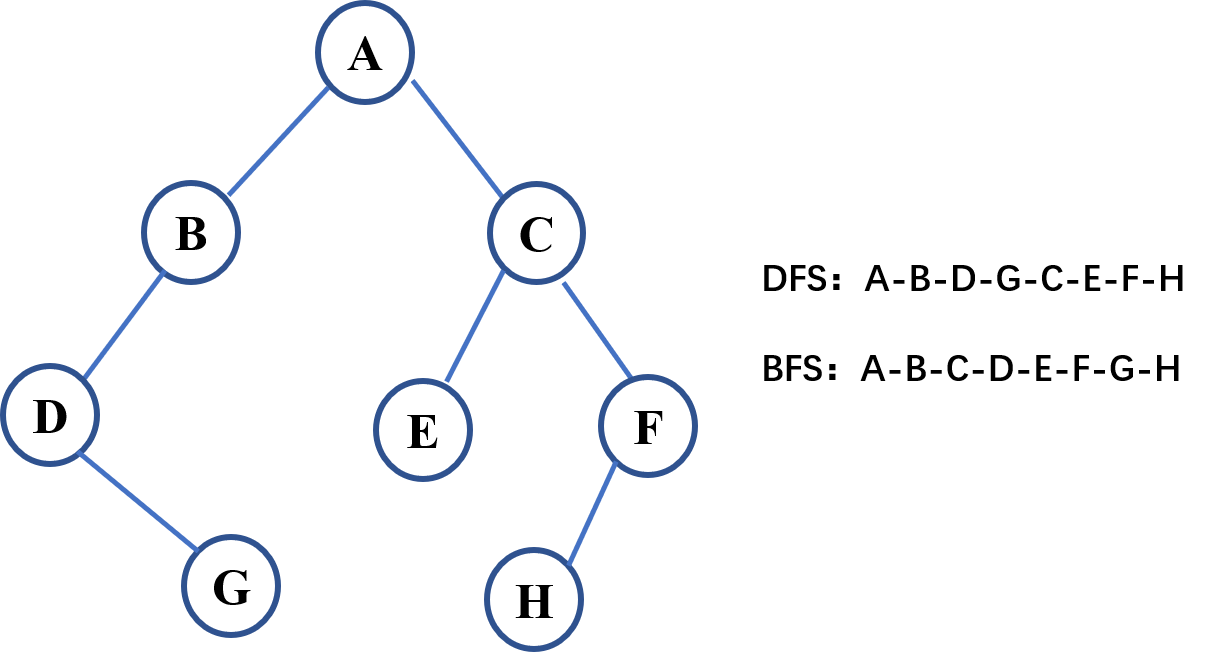
如果说广度优先是以中心向四周扩散的圆形方式寻找，深度优先就是一条线的一直找下去。深度优先不断的寻找未经过的相邻节点，直到不再有可遍历的相邻节点才会考虑回退到上一个节点并再换一个方向找。

深度优先算法其实更适合在树种的查找，而在图中特别是当一些图的节点是全连通的时候，深度优先就很难用了。

贪心算法

贪心算法适用于路径带有不同权值的时候，遍历时我们优先遍历相邻结点中权值较小者，这样做的好处是如果找到了路径，那么我们的路径一定是部分最短的（相邻结点永远是最短的，虽然不一定是全局最短，但是相对来说不会是最差的）

---

引入权重

现在我们要为寻路算法引入权重值，每个结点的权重值不一样，权重值由起点和终点的距离决定，权重越小则距离越小。

Dijkstra算法

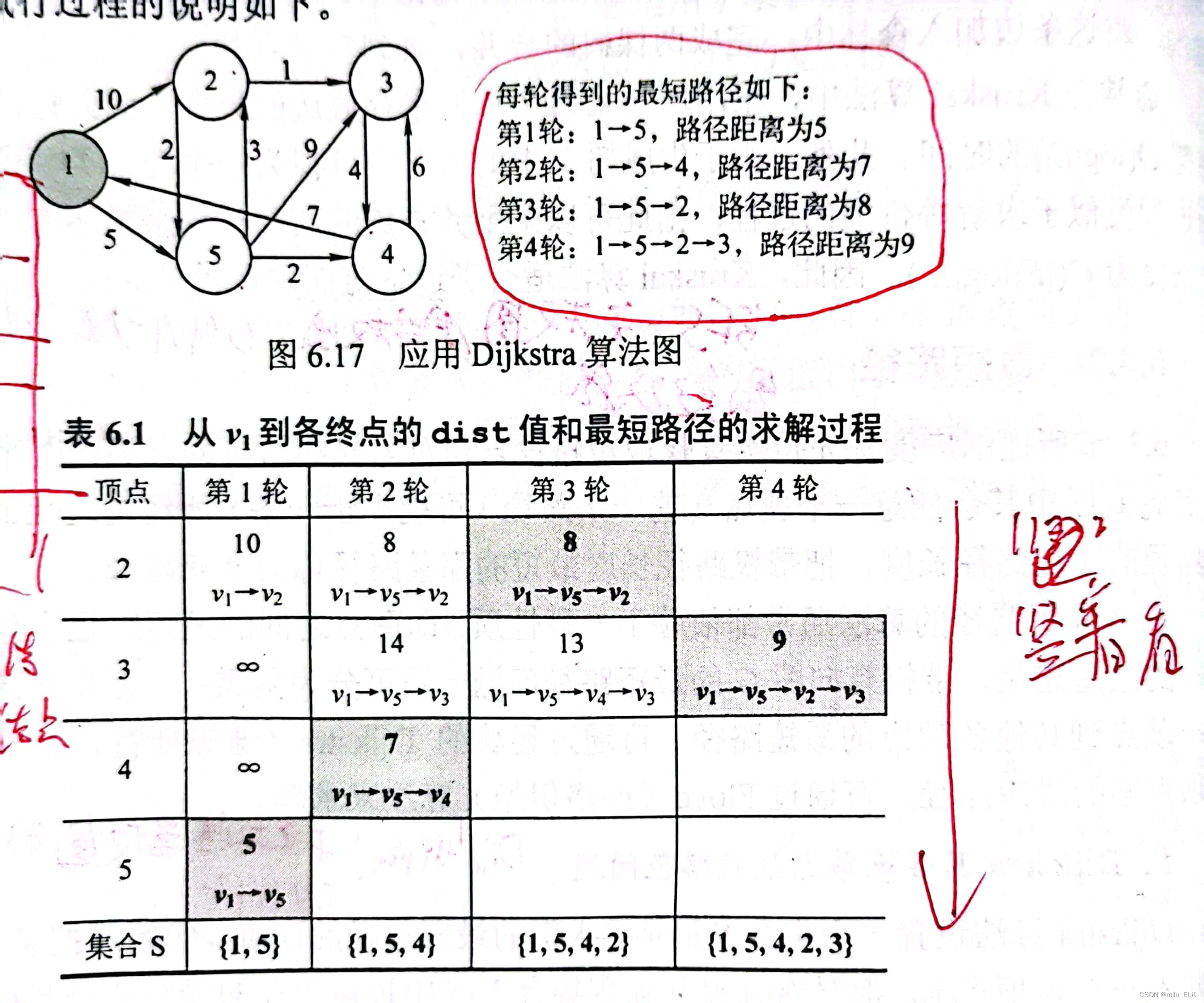
Dijkstra算法的原理是先算出起始点到其他点的最短路径，再求解。

例如以上图点1到点3为例，第一轮中找到点1到相邻点的最短路径是v1-v5，cost为5。那么我们就按着这个最短路径走，接着第二轮从点v5开始计算v5到其他点的路径长度。依次类推，按照表格上的路径，在第二轮发现v4达到不了v3，因此我们放弃这条路径，再次回到第二轮，选择除了这条路径以外最短的，也就是v1-v5-v2，按照这条路径走发现是可以到达v3的，此时就是我们的最短路径。

当找不到最短路径时，就要回退到本轮的第二短，本轮第二短达不到就第三短…以此类推。若本轮所有路径都不可达，那就回退到上一轮，选择上一轮中未选择的路径。

当图为网格图，且每个结点之间的移动代价相等时，Dijkstra就等于广度优先

---

现在让我们引入权值计算公式：默认权值为起点和终点间的距离
$abs(start.x-end.x)+abs(start.y-end.y)$

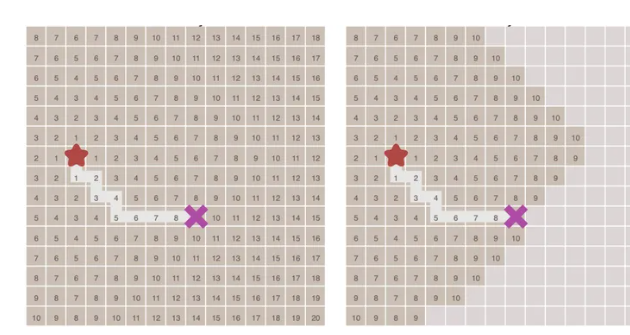
对比Dijkstra算法和贪心算法，在简单的情况下贪心算法更有优势：

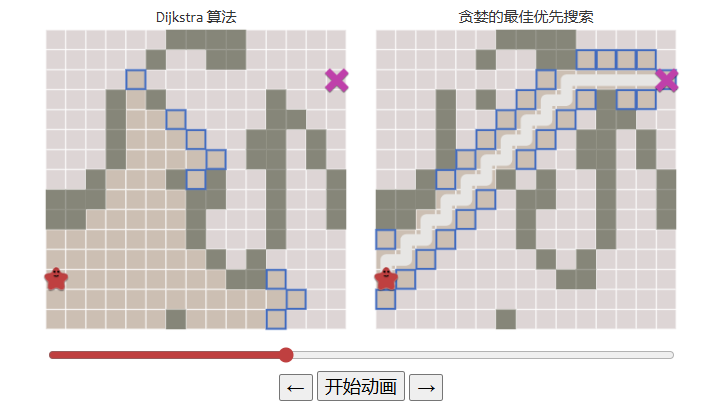
而一旦出现了复杂的地形，贪心算法就不一定是有效的了：

---

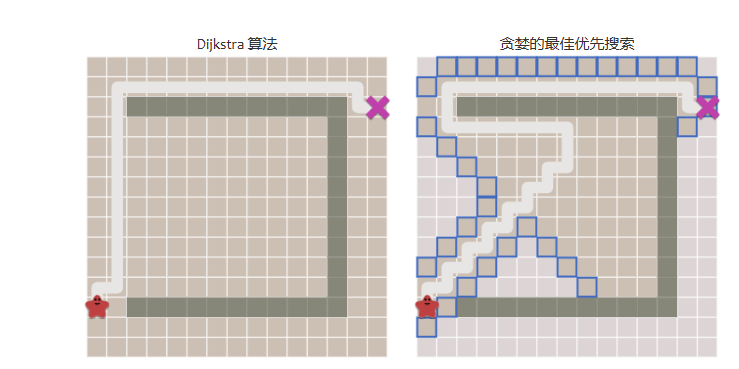
A*算法

之前讲了这么多，介绍了一些常见的寻路算法。Dijkstra效果好但是可能造成时间上的浪费，贪心算法速度快，但是最终的结果不一定是最短路径。

因此我们要学习A*算法：

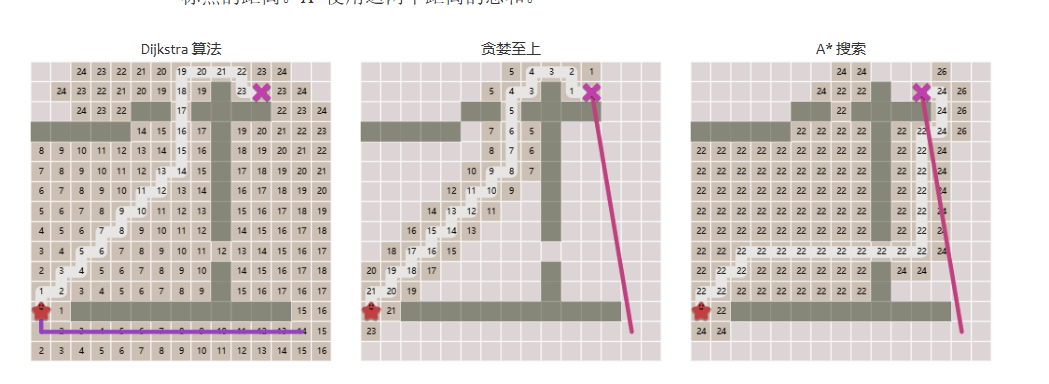
在A*算法下，找到的路径长度将是最短的，且用时要比Dijkstra算法要小。

A*算法是一种启发式算法，它通过这个函数来计算每个结点的优先级：

$f(n)=g(n)+h(n)$

其中

• f(n)是节点n的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。
• g(n) 是节点n距离起点的代价。
• h(n)是节点n距离终点的预计代价，这也就是A*算法的启发函数。关于启发函数我们在下面详细讲解。

A*算法在运算过程中，每次从优先队列中选取f(n)值最小（优先级最高）的结点作为下一个待遍历的节点。而不是类似Dijkstra算法，每次遍历相邻结点时尽管下一个结点可能出现权值过大的情况，但是我们不能确保它不是全局最优的，因此我们依然要把它加入到遍历路径中。

而相比下贪心算法虽然局部最优，但也不能确保是全局最优解。

A*算法的高明之处在于，除了实际代价，还有预估代价作为参考，当遍历结点越接近终点，则$g(n)越大，h(n)越小$,因此往往在最短路径上的结点值$f(n)$相差不大。因此我们可以用贪心算法选取优先路径，再用Dijkstra进行遍历。遍历的节点数量也小于Dijkstra算法 。

如果选取的启发函数有问题，那么结果可能更偏向Dijkstra算法。

---

C#实现

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
原文链接：https://blog.csdn.net/qq_60125117/article/details/130233023

转自C# A*算法，总结的太好了，我就直接抄了

A*算法使用一个开放列表(open list)和一个封闭列表(closed list)来维护搜索过程。开放列表存储待扩展的节点，而封闭列表存储已经扩展过的节点，以避免重复扩展节点。

在搜索过程中，我们从开放列表中选择f值最小的节点进行扩展，并将其加入封闭列表中。如果该节点是目标状态，则搜索结束，并返回从起点到目标状态的最短路径。

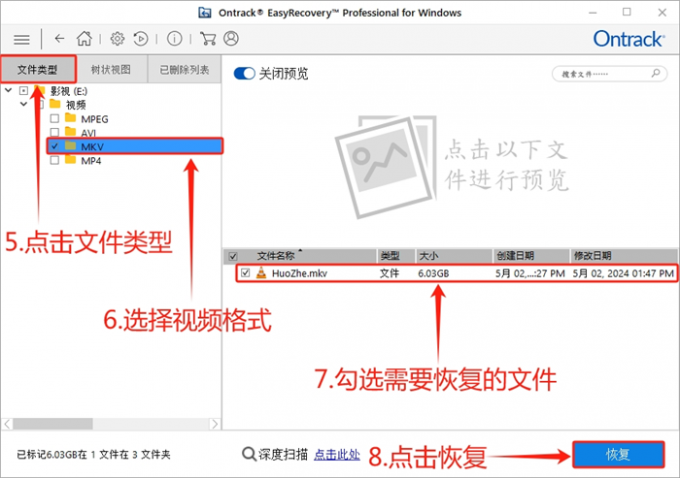
步骤

1. 将起点加入开放列表，并将其代价设置为0。
2. 从开放列表中选择代价$f(n)$值最小的节点进行扩展，即优先选择离目标状态更接近的节点。
3. 将该节点从开放列表中移除，并加入封闭列表中。
4. 对该节点的所有相邻节点进行以下操作：
   1. 如果该节点已经在封闭列表中，则忽略该节点
   2. 如果该节点不在开放列表中，则将其加入开放列表，并将其代价和父节点设置为当前节点
   3. 如果该节点已经在开放列表中，则比较当前节点到该节点的代价和已有的代价，选择代价较小的路径，并更新该节点的代价和父节点。
5. 重复步骤2-4，直到开放列表为空或找到目标状态。
6. 如果找到目标状态，则从目标状态开始回溯路径，直到回溯到初始状态。

public List<Node> FindPath(Node start, Node end)
{
    // 存储已访问的节点
    var closedSet = new HashSet<Node>();
    // 存储待访问的节点
    var openSet = new Heap<Node>(nodeComparer);
    openSet.Add(start);
 
    // 存储节点到起点的实际代价
    var gScore = new Dictionary<Node, float>();
    gScore[start] = 0;
 
    // 存储节点到终点的估计代价
    var hScore = new Dictionary<Node, float>();
    hScore[start] = HeuristicCostEstimate(start, end);
 
    // 存储每个节点的父节点，用于回溯路径
    var cameFrom = new Dictionary<Node, Node>();
 
    while (openSet.Count > 0)
    {
        // 获取最小估价的节点
        var current = openSet.RemoveFirst();
 
        if (current == end)
        {
            // 找到目标状态，回溯路径
            var path = new List<Node>();
            while (current != start)
            {
                path.Add(current);
                current = cameFrom[current];
            }
            path.Reverse();
            return path;
        }
 
        // 标记当前节点已访问
        closedSet.Add(current);
 
        // 遍历当前节点的相邻节点
        foreach (var neighbor in current.Neighbors)
        {
            if (closedSet.Contains(neighbor))
                continue; // 相邻节点已经访问过了
 
            // 计算当前节点到相邻节点的实际代价
            // 关于代价函数t(n)=g(n)+h(n)，其中启发函数h(n)是可以自定义的，只要效果好就行
            var tentativeGScore = gScore[current] + DistanceBetween(current, neighbor);
 
            // 如果相邻节点不在待访问列表中，或者到相邻节点的代价更小
            if (!openSet.Contains(neighbor) || tentativeGScore < gScore[neighbor])
            {
                // 更新相邻节点的父节点和代价
                cameFrom[neighbor] = current;
                gScore[neighbor] = tentativeGScore;
                hScore[neighbor] = HeuristicCostEstimate(neighbor, end);
 
                // 如果相邻节点不在待访问列表中，加入待访问列表
                if (!openSet.Contains(neighbor))
                    openSet.Add(neighbor);
            }
        }
    }
 
    // 找不到目标状态，返回空列表
    return new List<Node>();
}

找到最终结点后，我们只需要从终点开始，一路沿着相邻的OpenList结点中的最小值回溯即可找到寻路的路径。

---

Unity中的A*算法

Unity中的A算法是一种常用的寻路算法，用于计算在网格或图形地图上找到最短路径。A算法基于图搜索和启发式评估，具有较高的效率和准确性。

其实Unity中要使用A*算法，就是对地图模型的抽象，将其抽象为结点构成的图。我们可以分割网格，或者自定义结点坐标来实现。总之原理是一样的，就是需要抽象出结点的概念：

1. 创建网格或图形地图：将游戏场景分割为一系列网格或节点，并构建地图数据结构，用于存储每个节点的信息，如位置、连接关系和代价。
2. 定义节点的启发式评估函数：A*算法使用启发式函数来估计从当前节点到目标节点的代价。这个函数通常基于节点之间的距离或其他因素，用于指导搜索过程。
3. 实现Open列表和Closed列表：Open列表存储待评估的节点，Closed列表存储已评估过的节点。开始时，将起始节点添加到Open列表中。
4. 迭代搜索过程：循环执行以下步骤直到找到目标节点或Open列表为空：
   1. 从Open列表中选择代价最小的节点，作为当前节点。
   2. 将当前节点从Open列表中移除，并添加到Closed列表中。
   3. 检查当前节点是否为目标节点，如果是，则路径搜索完成。
   4. 否则，对当前节点的相邻节点进行遍历

A*算法的性能和效果受到地图复杂度、启发式函数的选择以及路径平滑等因素的影响。在实际使用中，可以根据具体需求对算法进行调优和优化

---

A*优化建议

如果需要对A*算法进行性能优化，可以考虑以下几点：

1. 使用优先队列：A*算法需要频繁地从开放列表中取出具有最小代价的节点，因此使用优先队列可以提高算法的效率。
2. 使用启发式算法：启发式算法可以在搜索过程中尽可能地快速地找到目标节点，从而提高算法效率。在实现过程中，需要设计一个好的估价函数，以便尽可能减少搜索的节点数。（好像炼丹啊）
3. 剪枝：A*算法中有一些无用的搜索节点，可以使用剪枝技术将其剪掉，从而减少搜索时间。
4. 预处理：预处理是指对搜索的地图进行预处理，以便在搜索过程中可以快速地获取地图信息，从而提高搜索效率。

还有一种针对静态地图的优化方法：使用预处理的路线图（Precomputed Roadmap）。

预处理的路线图是一种离线生成的数据结构，它将地图划分为一些相互连接的区域，并计算出每个区域之间的最短路径。在搜索过程中，可以直接使用预处理的路线图，从而避免了大量的搜索操作。