二叉树的链式访问与二叉树专题

news2024/10/6 2:28:08

二叉树的前、中、后序遍历

1.前序遍历：先访问根节点，再访问左子树，最后访问右子树
根左右
2.中序遍历：先访问左子树，再访问根，最后访问右子树
左根右
3.后序遍历：先访问左子树，再访问右子树，最后访问根
左右根

N 表示 NULL
前序访问顺序：1 2 3 N N N 4 5 N N 6 N N
中序访问顺序：N 3 N 2 N 1 N 5 N 4 N 6 N
后序访问顺序：N N 3 N 2 N N 5 N N 6 4 1
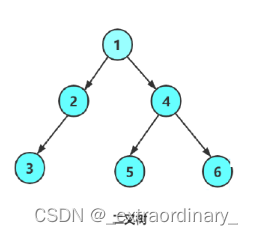
在这里插入图片描述

求二叉树第K层节点的个数

子问题是：root不为空，k不等于1
转化为求左子树加右子树第三层的节点个数
每层k都减1，如果该层有root == NULL就返回0
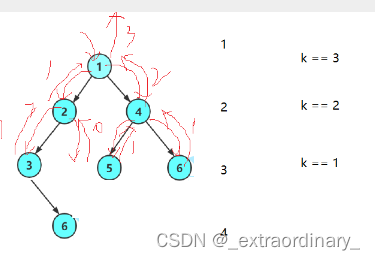
在这里插入图片描述


//求二叉树第k层的节点个数 
int TreeLevelKSize(BTNode* root,int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;

return TreeLevelKSize(root->left, k-1) + TreeLevelKSize(root->right, k-1);
}

二叉树查找值为x的节点

找到一个值为x的节点就返回，因为函数只有一个返回值
return 只能返回给上一层
如果找到了不存入一个变量中，找到的值就会重复找（后面会丢失找到的值）

//二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->val == x)
		return root;
	//只能返回给它的上一层

	//前序遍历
	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)
		return ret1;

	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
		return ret2;

	//都没找到
	return NULL;
}

leetcode相同的树

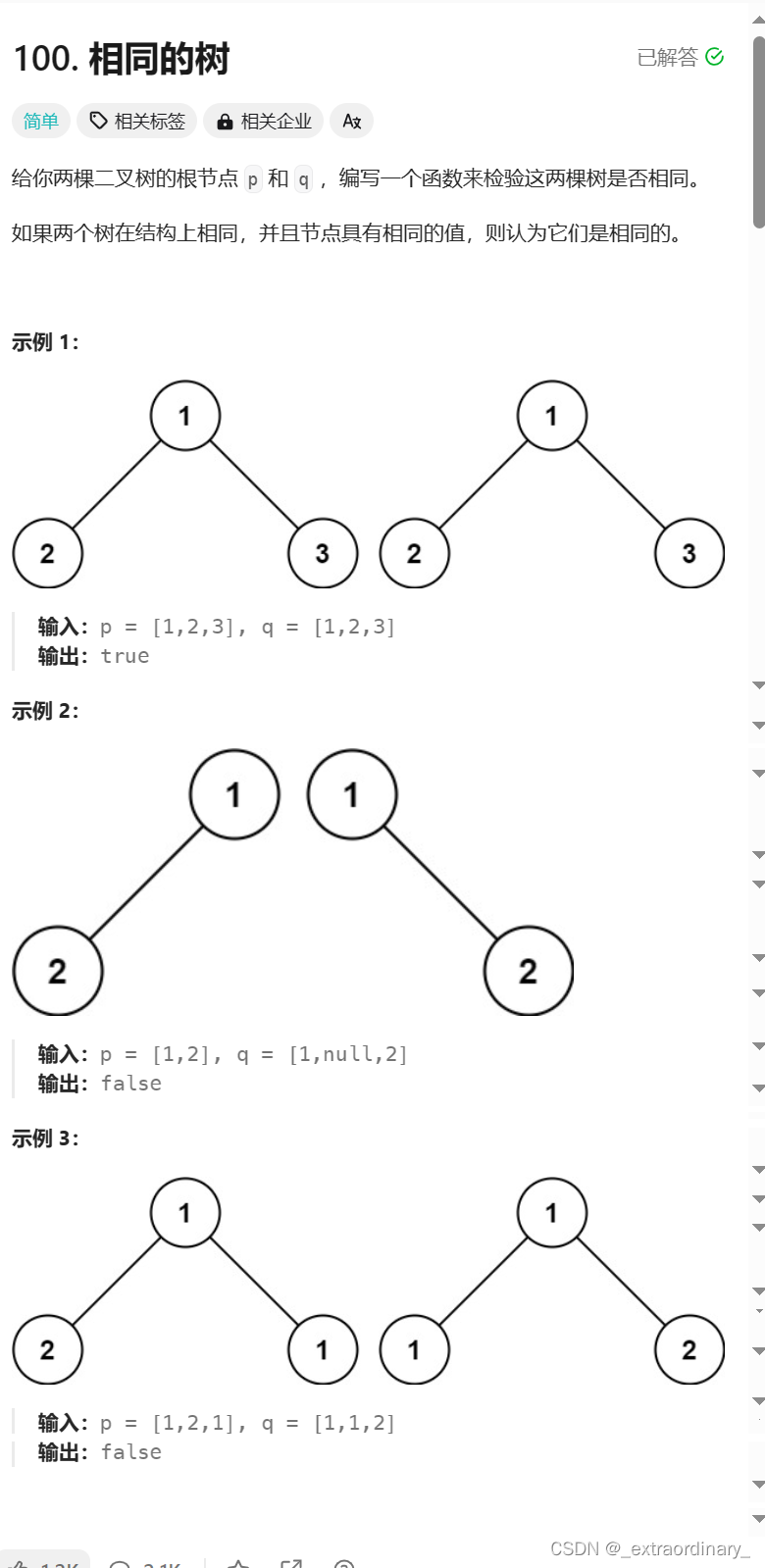
在这里插入图片描述
思路：
比较两棵树的根，左子树和右子树是否相等
1.两棵树的根都为NULL,返回true
2.其中一棵树的根为NULL,两树的节点不相同返回false
3.两树的根都不为NULL,比较两树的根的值
4.子问题：遍历两树的左子树和右子树（比较左根和右根）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    if(p == NULL&&q == NULL)
    return true;

    //其中一个节点为空，另一个节点不为空，返回false
    if(p == NULL || q == NULL)
    return false;

    //两个节点都不为空
    if(p->val != q->val)
    return false;

    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

对称二叉树

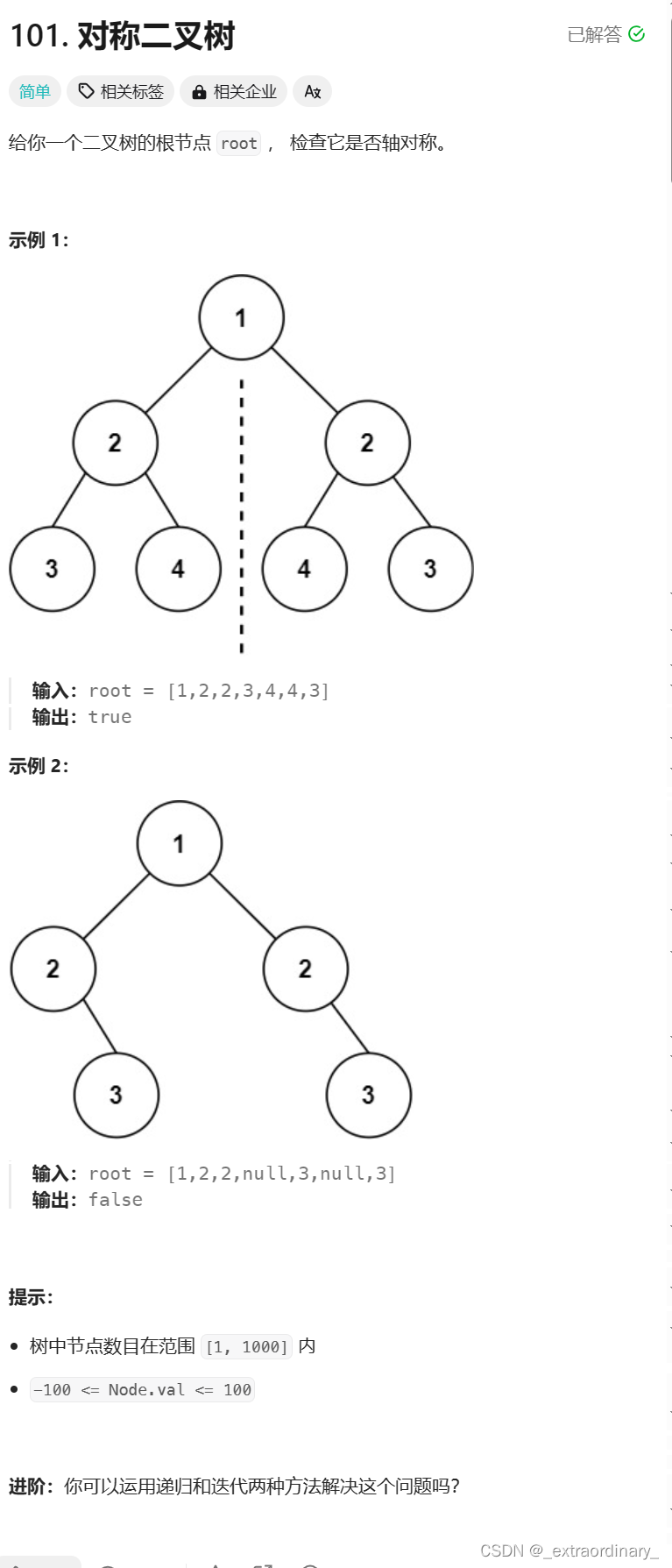
在这里插入图片描述
思路：
这题和上一题很想，可以理解为镜像二叉树（即一棵树的左子树和右子树要一样，一棵树的右子树和左子树要一样）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool _isSymmetric(struct TreeNode* p,struct TreeNode* q)
{
    if(p == NULL&&q == NULL)
    return true;
    
    if(p == NULL||q == NULL)
    return false;

    if(p->val != q->val)
    return false;

    return _isSymmetric(p->left,q->right)&&_isSymmetric(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root) 
{
    return _isSymmetric(root->left,root->right);
}

二叉树的前序遍历

在这里插入图片描述
思路：
1.先算出二叉树中有多少个节点，再开辟这么多个节点
这样不会造成空间不足或空间浪费
2.i 是数组的下标，要用指针传递过去，不用指针的话，形参i的改变不会影响实参i,可能会覆盖前面的值
在这里插入图片描述
3.前序遍历，如果有节点就把节点中的值放入数组中，如果没有就返回NULL,遵循根左右依次把值放入数组中

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
//算出树的节点个数
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//前序遍历
void preorder(struct TreeNode* root,int* arr,int* pi)
{
    if(root == NULL)
    return;

    arr[(*pi)++] = root->val;
    preorder(root->left,arr,pi);
    preorder(root->right,arr,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    *returnSize = TreeSize(root);
    int* arr = (int*)malloc(sizeof(int)*(*returnSize));

    //前序遍历
    int i = 0;
    //下标是一个小坑，如果不用指针，每次递归调用i的值是形参有时会覆盖前面的值
    preorder(root,arr,&i);

    return arr;
}

另一棵子树

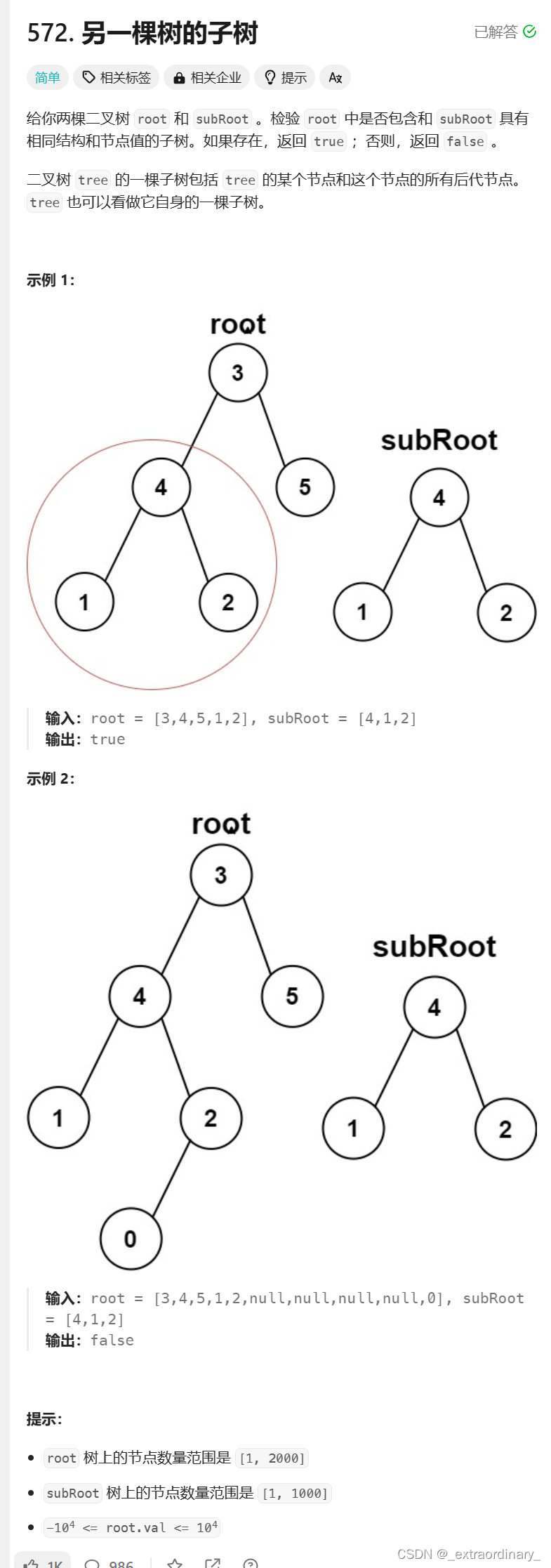
在这里插入图片描述
思路：
1.root在走，直到root == NULL都没找到值和subRoot相同的节点，那么就返回false
2.如果能找到和root相同的节点，那么比较root后面的节点（子树中）是否和subRoot相同
3.只要找到一个子树是和subRoot相同的那么就返回true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

//这里面子树与另一题两个子树是否相同有一样的逻辑
bool issametree(struct TreeNode* p,struct TreeNode* q)
{
    if(p == NULL&&q == NULL)
    return true;

    if(p == NULL || q == NULL)
    return false;

    if(p->val != q->val)
    return false;

    return issametree(p->left,q->left) && issametree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    //subRoot不为空,使用root在递归，所以root可能会走到空false
    //subRoot至少有一个节点
    if(root == NULL)
    return false;

    if(root->val == subRoot->val&&
    issametree(root,subRoot))
    return true;
    
    //root在走，subRoot不走，之后利用root和subRoot相等的节点，再用issametree比较是否是子树
    return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

牛客二叉树的遍历

在这里插入图片描述
思路：
总体来说是先开一个100个字符的字符串数组，然后构建节点，最后中序遍历打印数组
1.构建节点时要注意如果root == ‘#’时，不能在判断的时候（*pi）++,如果它不是‘#’的话还++就跳过一个字符了
2.开1个节点的树，就把数组中的值放入树中，然后为左树和右树开辟一个节点，最后返回根节点，把各个节点链接起来，return root是为了链接节点

#include <stdio.h>
#include<stdlib.h>

typedef struct TreeNode
{ 
   struct TreeNode* left;
   struct TreeNode* right;
   int val;
}TreeNode;
//构建节点
TreeNode* CreatTree(char* a,int* pi)
{
    if(a[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    
    //非空
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
    root->val = a[(*pi)++];
    //下面这里没有想出来,递归root的左边创建一个节点,
    //然后递归root的右边创建一个节点，
    //最后返回根，链接起来
    root->left = CreatTree(a,pi);
    root->right = CreatTree(a,pi);

    return root;
}
//中序遍历
void order(TreeNode* root)
{
    if(root == NULL)
    return;

    order(root->left);
    printf("%c ",root->val);
    order(root->right);
}
int main() 
{
    char a[100];
    scanf("%s",a);

    int i = 0;
    TreeNode* ret = CreatTree(a,&i);
    order(ret);

    return 0;
}