前言
思路及算法思维,指路 代码随想录。
题目来自 LeetCode。
day 55,又是一个周一,不能再坚持~
题目详情
[42] 接雨水
题目描述
42 接雨水

解题思路
前提:雨水形成的情况是凹的, 需要前中后3个元素,计算该元素左右两侧的第一个大于该高度的高度
思路:单调递增栈
重点:单调栈的思维
代码实现
C语言
单调递增栈
单调递增栈: 【横向计算形成凹行柱体的雨水】
雨水形成的情况是凹的, 需要当前新的栈顶元素, 计算的是旧的栈顶元素形成的雨水
// 单调递增栈: 雨水形成的情况是凹的, 需要当前新的栈顶元素, 计算的是旧的栈顶元素形成的雨水
int minFun(int p1, int p2)
{
return p1 < p2 ? p1 : p2;
}
int trap(int* height, int heightSize) {
int stack[heightSize];
int top = 0;
// 遍历计算每个柱子接到的雨水之和
int sum = 0;
for (int i = 0; i < heightSize; i++) {
// 单调递增栈
// 当前元素比栈顶元素大,不满足单调递增栈的要求
while (top > 0 && height[i] > height[stack[top - 1]]) {
// 弹出当前栈顶元素
int midIndex = stack[top - 1];
top--;
// 雨水形成的情况是凹的, 需要当前新的栈顶元素, 计算的是旧的栈顶元素形成的雨水
if (top > 0) {
int leftIndex = stack[top - 1];
sum += (minFun(height[leftIndex], height[i]) - height[midIndex]) * (i - leftIndex - 1);
}
}
stack[top] = i;
top++;
}
return sum;
}
双指针
双指针解法:【竖向计算每个柱体形成的雨水】
两次遍历求当前左侧最高柱子高度maxLeft[i]和右侧最高柱子高度maxRight[i]
// 双指针解法:两次遍历求当前左侧最高柱子高度maxLeft[i]和右侧最高柱子高度maxRight[i]
int maxFun(int p1, int p2)
{
return p1 > p2 ? p1 : p2;
}
int minFun(int p1, int p2)
{
return p1 < p2 ? p1 : p2;
}
int trap(int* height, int heightSize) {
int maxLeft[heightSize];
int maxRight[heightSize];
// 遍历搜索左侧最高柱子高度
maxLeft[0] = height[0];
for (int i = 1; i < heightSize; i++) {
maxLeft[i] = maxFun(height[i], maxLeft[i - 1]);
}
// 遍历搜索右侧最高柱子高度
maxRight[heightSize - 1] = height[heightSize - 1];
for (int j = heightSize - 2; j >= 0; j--) {
maxRight[j] = maxFun(height[j], maxRight[j + 1]);
}
// 遍历计算每个柱子接到的雨水之和
int sum = 0;
for (int k = 0; k < heightSize; k++) {
sum += minFun(maxLeft[k], maxRight[k]) - height[k];
}
return sum;
}
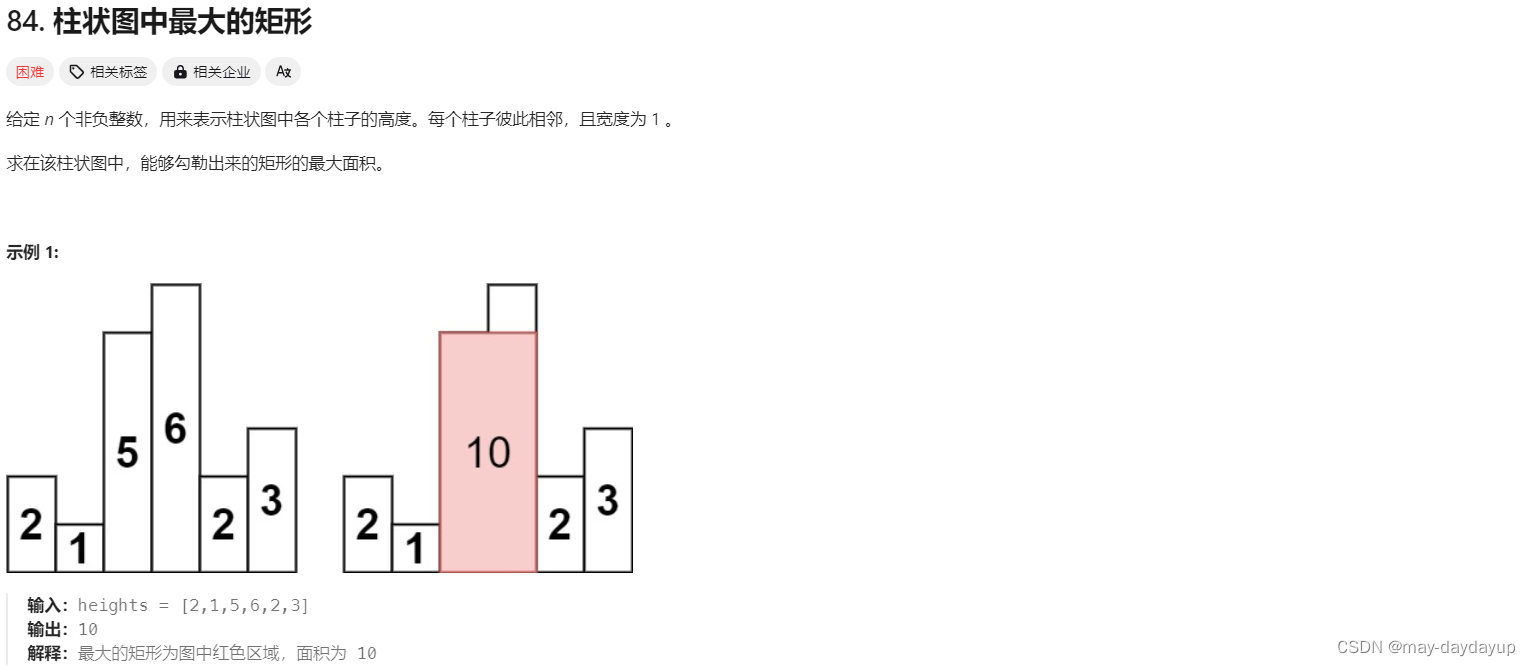
[84] 柱状图中最大的矩形
题目描述
84 柱状图中最大的矩形
解题思路
前提:柱状图形成的最大面积,需要求解该柱子左右两侧 最远>=该柱子高度的柱子宽度,即可以求解该柱子左右两侧小于该柱子高度的位置,进而计算所求宽度
思路:单调递减栈
重点:单调栈的思维
代码实现
C语言
单调递减栈
// 单调递减栈: 寻找该柱子左右两侧第一个小于该柱子高度的柱子, 即可找到最后左右两侧最远一个大于该柱子高度的连续柱子, 计算所形成的的最大面积
// 栈顶到栈底,元素依次递减
int minFun(int p1, int p2)
{
return p1 < p2 ? p1 : p2;
}
int maxFun(int p1, int p2)
{
return p1 > p2 ? p1 : p2;
}
int largestRectangleArea(int* heights, int heightsSize) {
int stack[heightsSize];
int top = 0;
int maxSum = 0;
// 遍历
for (int i = 0; i < heightsSize; i++) {
// 寻找查找栈顶柱子的右侧第一个低于栈顶柱子的柱子位置
while (top > 0 && heights[i] < heights[stack[top - 1]]) {
// 弹出栈顶元素
int midIndex = stack[top - 1];
top--;
// 计算弹出元素所形成的凸型的面积
// 判断是否形成凸的最左侧
int leftIndex = 0;
if (top > 0) {
leftIndex = stack[top - 1] + 1;
}
int rightIndex = i - 1;
int sum = heights[midIndex] * (rightIndex - leftIndex + 1);
maxSum = maxFun(maxSum, sum);
}
stack[top] = i;
top++;
}
// 判断是否最后没有形成凸的最右侧,清空栈
while (top > 0)
{
int midIndex = stack[top - 1];
top--;
if (top == 0) {
// 此时这个元素为当前元素数组中最小的元素
int sum = heights[midIndex] * heightsSize;
maxSum = maxFun(maxSum, sum);
} else {
// 此时单调栈中元素递减
int sum = heights[midIndex] * ((heightsSize - 1) - (stack[top - 1] + 1) + 1);
maxSum = maxFun(maxSum, sum);
}
}
return maxSum;
}
针对数组单调递增等不能形成凸型的特殊情况, 需要特殊处理,
所以在原数组首尾添加最小元素0, 以便对原数组做同一处理。
优化代码如下。
// 单调递减栈: 寻找该柱子左右两侧第一个小于该柱子高度的柱子, 即可找到最后左右两侧最远一个大于该柱子高度的连续柱子, 计算所形成的的最大面积
// 栈顶到栈底,元素依次递减
// 针对数组单调递增等的特殊情况, 需要特殊处理,所以在原数组首尾添加最小元素0,以便对原数组做同一处理
int maxFun(int p1, int p2)
{
return p1 > p2 ? p1 : p2;
}
int largestRectangleArea(int* heights, int heightsSize) {
int newHeightsSize = heightsSize + 2;
int newHeights[newHeightsSize];
newHeights[0] = 0;
newHeights[newHeightsSize - 1] = 0;
for (int t = 1; t < newHeightsSize - 1; t++) {
newHeights[t] = heights[t - 1];
}
int stack[newHeightsSize];
int top = 0;
int maxSum = 0;
// 遍历
for (int i = 0; i < newHeightsSize; i++) {
// 寻找查找栈顶柱子的右侧第一个低于栈顶柱子的柱子位置
// 当遍历到新数组的最后一个元素0, 必可以进入该循环进行处理
while (top > 0 && newHeights[i] < newHeights[stack[top - 1]]) {
// 弹出栈顶元素
int midIndex = stack[top - 1];
top--;
// 计算弹出元素所形成的凹型的面积
// 此处的栈中必有新数组的首元素0
int leftIndex = stack[top - 1] + 1;
int rightIndex = i - 1;
int sum = newHeights[midIndex] * (rightIndex - leftIndex + 1);
maxSum = maxFun(maxSum, sum);
}
stack[top] = i;
top++;
}
return maxSum;
}
双指针
寻找该柱子左侧的第一个小于该柱子的高度的下标minLeftIndex[i] 和 右侧第一个小于该柱子的高度的下标minRightIndex[i],
进而计算不小于该柱子高度的连续长度。
// 双指针方法: 寻找该柱子左侧的第一个小于该柱子的高度的下标minLeftIndex[i] 和 右侧第一个小于该柱子的高度的下标minRightIndex[i]
// 计算以当前柱子形成凹形状的柱子的最大面积
int minFun(int p1, int p2)
{
return p1 < p2 ? p1 : p2;
}
int maxFun(int p1, int p2)
{
return p1 > p2 ? p1 : p2;
}
int largestRectangleArea(int* heights, int heightsSize) {
int minLeftIndex[heightsSize];
int minRightIndex[heightsSize];
// 遍历,寻找该柱子左侧的第一个小于该柱子的高度的下标
minLeftIndex[0] = -1;
for (int i = 1; i < heightsSize; i++) {
int t = i - 1;
// 查找左侧第一个小于该柱子高度的柱子下标
while (t >= 0 && heights[t] >= heights[i]) {
t = minLeftIndex[t];
}
minLeftIndex[i] = t;
}
// 遍历,寻找该柱子右侧的第一个小于该柱子的高度的下标
minRightIndex[heightsSize - 1] = heightsSize;
for (int j = heightsSize - 2; j >= 0; j--) {
int t = j + 1;
// 查找右侧第一个小于该柱子高度的柱子下标
while (t < heightsSize && heights[t] >= heights[j]) {
t = minRightIndex[t];
}
minRightIndex[j] = t;
}
// 遍历寻找最大面积
int sum = 0;
int maxSum = 0;
for (int k = 0; k < heightsSize; k++) {
// 求以当前柱子形成凹形状的柱子的最大面积
int leftIndex = minLeftIndex[k] + 1;
int rightIndex = minRightIndex[k] - 1;
sum = heights[k] * (rightIndex - leftIndex + 1);
maxSum = maxFun(maxSum, sum);
}
return maxSum;
}
今日收获
- 单调栈,以及为了使用单调栈所做的变化