交换机需要多大 buffer

news2024/10/7 9:28:03

有点违背直觉，但是真事儿，交换机过境的流越多，所需 buffer 越小，这是为什么？

范氏(范雅各布森，van jacobson)管道的 aimd 流建议 buffer_size 为 bdp，这很容易理解，因为 aimd 流最小 cwnd 为最大 cwnd 的 1/2，为保持管道持续满载，1/2 * cwnd 填满管道即可，即 1/2 * cwnd = bdp，因此 buffer_size = cwnd_max = 2 * bdp。

但这是单流的推导，多流共享 buffer 场景下是否适用还要继续推导。若 buffer 配置尾丢(tail drop)，多流全局同步，范氏 style 推导依然适用，但若 buffer 配置为 red(random early detection) or codel，就要更复杂些，我先给出一个极端些的直感，再稍微详细分析随机异步流共享 buffer 场景。
所谓的极端即所有流 “均匀摊布” 在时间轴：
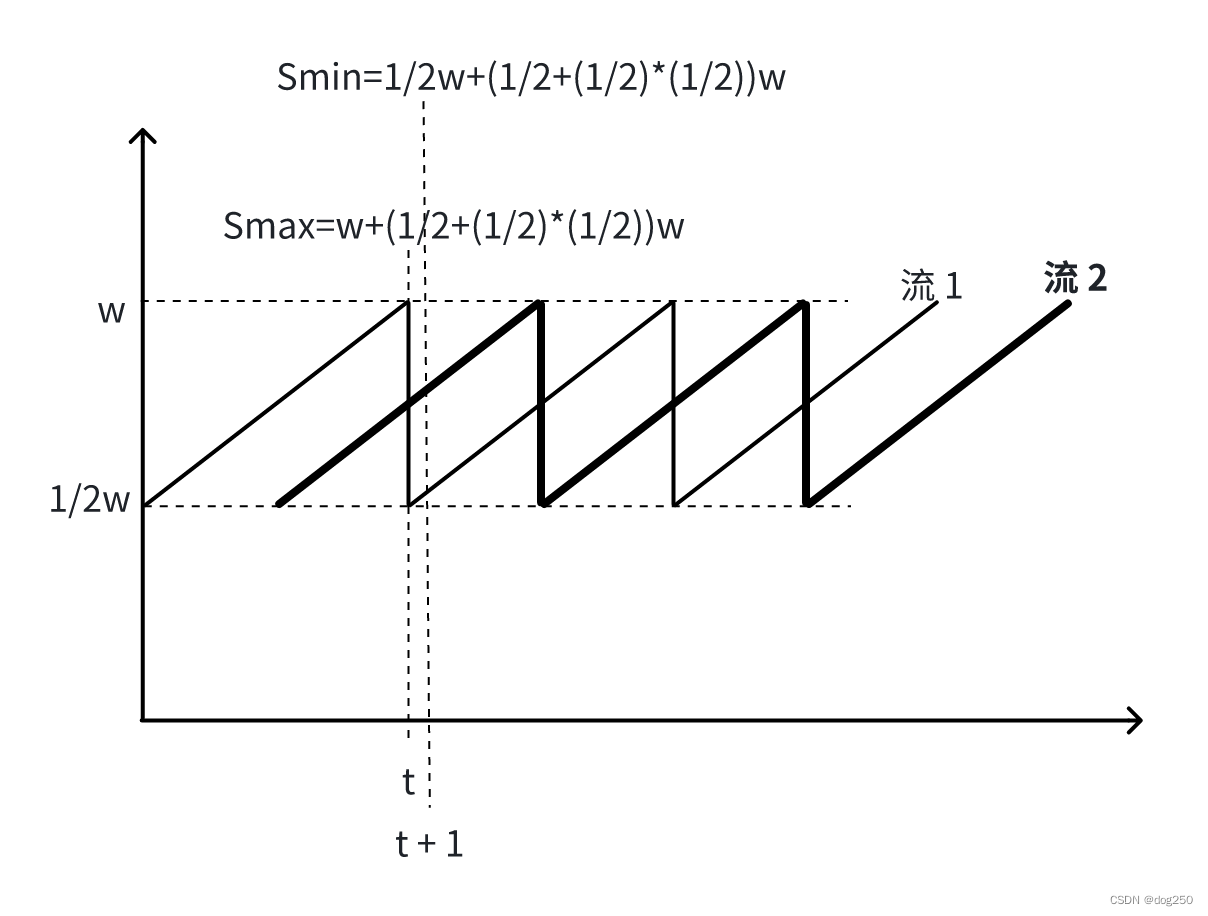
在这里插入图片描述

如上图两条流均匀摊布场景，两条流 cwnd 之和在其中一流 md 后即 t + 1 时刻获得，此时它们的 cwnd 之和为 Smin = 1 / 2w + (1 / 2 + (1 / 2) * (1 / 2))w，为保持管道满载，只需要让 Smin = bdp，而 buffer 的大小保持为 Smax - Smin 即可。

按此推广到 n 条流均匀摊布，可得：

$S_{min}=\dfrac{1}{2}w+(\dfrac{1}{2}+\dfrac{1}{2}\cdot\dfrac{1}{n})w+(\dfrac{1}{2}+\dfrac{1}{2}\cdot\dfrac{2}{n})w+...+(\dfrac{1}{2}+\dfrac{1}{2}\cdot\dfrac{n-1}{n})w$

化简可得：

$S_{min}= \dfrac{n}{2}\cdot w = bdp，w = bdp\cdot\dfrac{2}{n}$

而 Smax - Smin = (1 / 2)w，故 buffer_size = bdp / n。

这意味着 n 条流均匀摊布时，只需要保持 bdp / n 大小的 buffer 就能保持管道满载。

buffer 按流数量缩小难道这不会造成丢包加剧？持这种执念的人还是将 buffer 当带宽了，这是错误的。如果 n 条流共享带宽，目标是 n 条流均分带宽，不是分享 buffer，这意味着它们 md 后 cwnd 必降到 bdp 以下，保持管道满载意思是 cwnd 总和维持在 bdp 以上，一条流 cwnd 降到 bdp 以下，总有流填充它空出的部分。

好，现在开始步入正题。

实际的统计复用场景中，每条流独立，多条流不可能均匀摊布，其 cwnd 之和属正态分布。n 条流 cwnd 之和，每条流相当于从 (1 / 2)w 到 w 抽样 cwnd，cwnd 属均匀分布，根据中心极限定理，cwnd 的和属正态分布，设 cwnd 抽样标准差 $\sigma_{cwnd}$ ，cwnd 之和标准差为 $\sigma_{S}$ $，则$ $n\cdot\sigma_{cwnd}^2=\sigma_{S}^2$ 。

每条流的 cwnd 值属于从 (1 / 2)w 到 w 的均匀分布，其标准差为 $\sigma_{cwnd}=\dfrac{w}{2\sqrt{12}}$ ，在 n 条流共存场景， $w=\dfrac{\Sigma^n w_i}{n}$ ，因此 $\sigma_{cwnd}=\dfrac{w}{2\sqrt{12}}=\dfrac{\Sigma^n w_i}{2\sqrt{12}n}$ ，方差叠加可得：

$\sigma_S=\sqrt{n}\sigma_{cwnd}=\dfrac{\Sigma^nw_i}{4\sqrt{3}\sqrt{n}}=\dfrac{bdp+buffer}{4\sqrt{3}\sqrt{n}}$

而我们看上述表达式意味着什么：
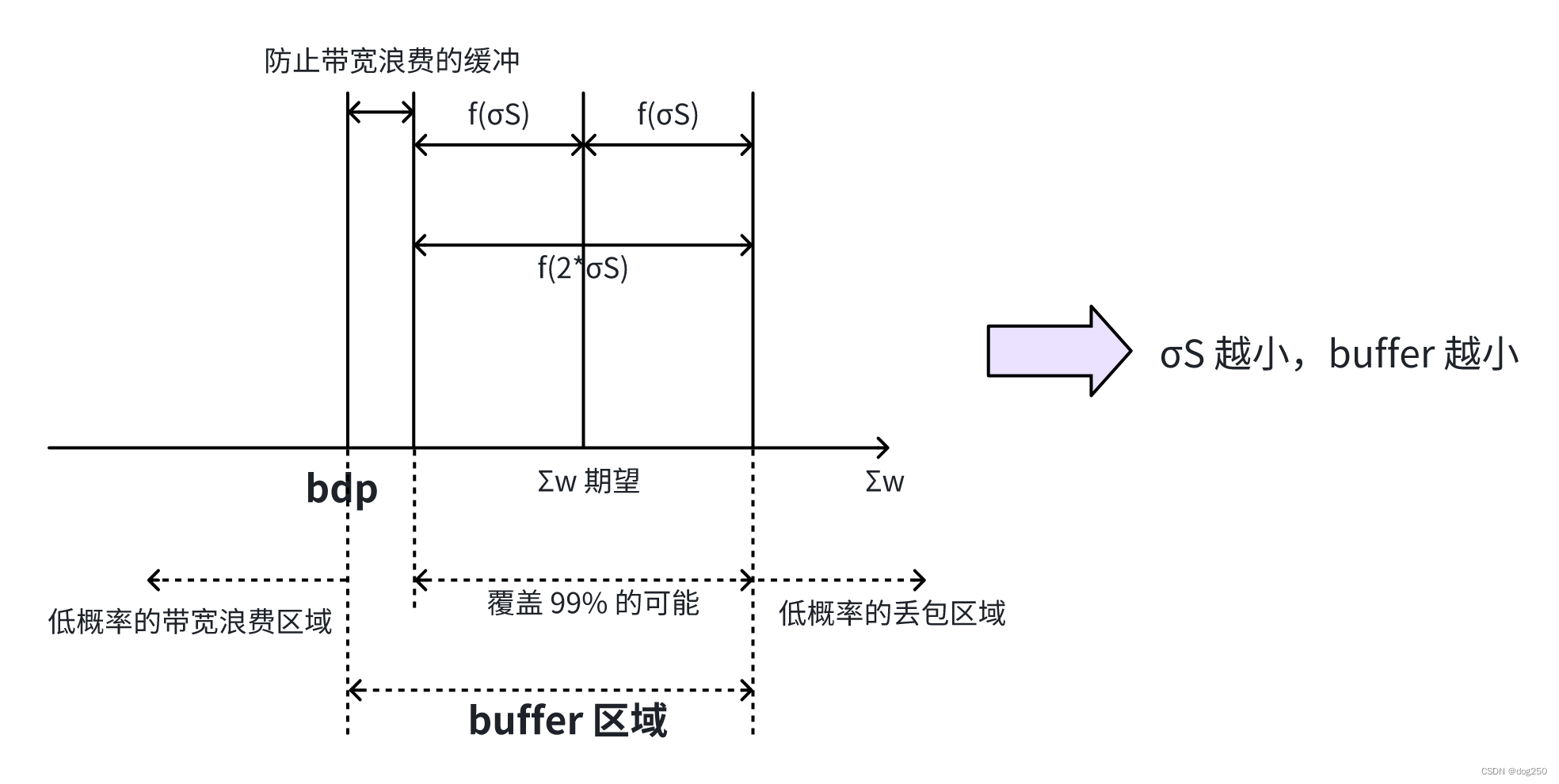
在这里插入图片描述

给定一个 buffer，n 越大，覆盖 99% 可能性的有用 buffer 越少，buffer 随着 sqrt{n} 缩小，整体上 buffer 被 n 往左边向 bdp 收缩。n 增大， $\sigma$ 减小，要让 $\sigma$ 减小，buffer 减小。

中心极限定理说的就是抽样越多钟形越高越细，抽样越多的意思就是 n 越大，随着 n 的增加，Σw 倾向于收敛到非常细高的区域，极端情况，n 无穷大，σS = 0，buffer 则不再需要，无穷条流的锯齿被平滑到 bdp 边缘，刚刚恰好填满 bdp。

依本文论点，aimd 锯齿仅在端可观测到，在交换机 buffer 的统计复用环境，多流行为效果恰就是中心极限定理 cwnd 采样求和的体现，依据的是另一种动力学。bbr 等 cc 分析应依据这种统计动力学而不是端侧的 aimd 动力学。

是故，足够大的 buffer 给了共存流量足够的腾挪折腾空间，其 buffer 挤占动力学有利于公平收敛，但也不绝对。buffer 过大，真带不来收益，带来时延而已，若不必吸收统计波动，仅固定数目 aimd 流共存，如上分析，实在无需大 buffer，流越多，buffer 用量越少即可保持管道满载。但现网部署的交换机配置稍微大的 buffer 实属吸收统计波动，比如 incast 或特殊事件(比如直播在特定时间开始后的短突发)，但即便是研发经理，恐怕也还是觉得任何场景下 buffer 越大越好吧。