在本文中，我们将深入训练过程，探讨神经网络到底是如何学习的。

内容很肝，建议收藏反复观看学习！

假设我们想创建一个神经网络，这个神经网络使用温度和星期几特征来预测每天冰淇淋的销售额。

这是我们使用的训练数据集：

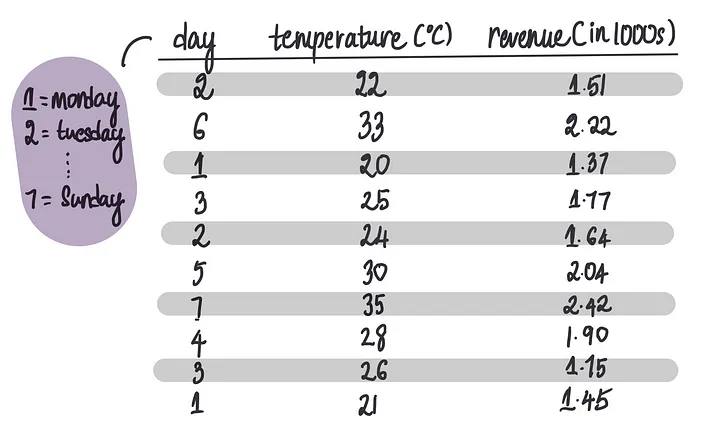
要构建一个神经网络，正如我们在之前的文章中学习的那样，我们首先需要确定其架构。

这包括确定隐藏层的数量、每层中的神经元数量以及每个神经元的激活函数。
假设我们决定使用以下架构：1个隐藏层、2个神经元，1个输出神经元，所有这些都使用整流器激活函数（ReLU）。

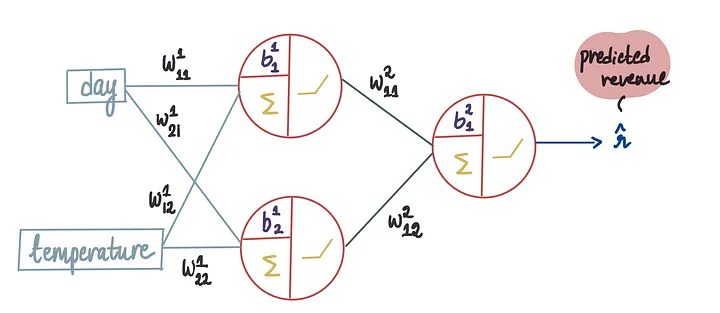
一旦我们确定了架构，就可以通过输入一些数据来训练模型了。

在这个训练过程中，神经网络将学习权重和偏置项的最优值。假设使用上面的训练数据训练模型后，它产生了以下最优值：

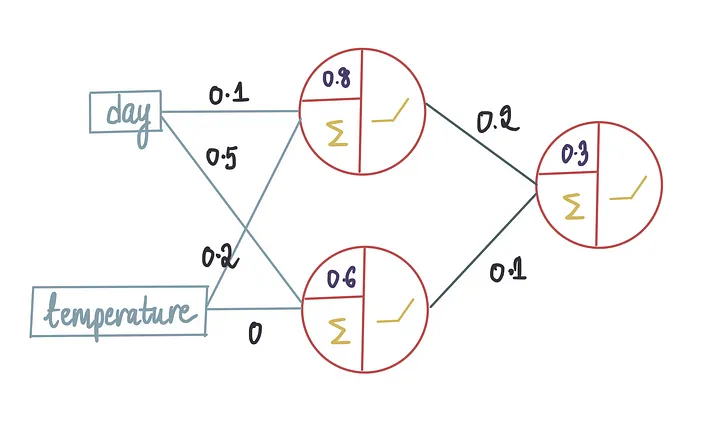
本文将重点介绍我们如何得到这些最优值。

让我们从一个简单的示例开始。假设我们有了所有最优值，除了外层神经元的偏置项。

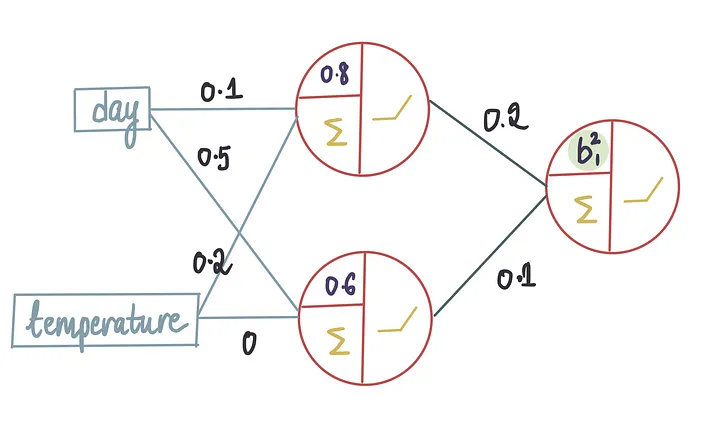
因为我们不知道偏置的确切值，所以我们首先进行初始猜测并将值设置为 0，通常，偏置值在开始时都被初始化为0。

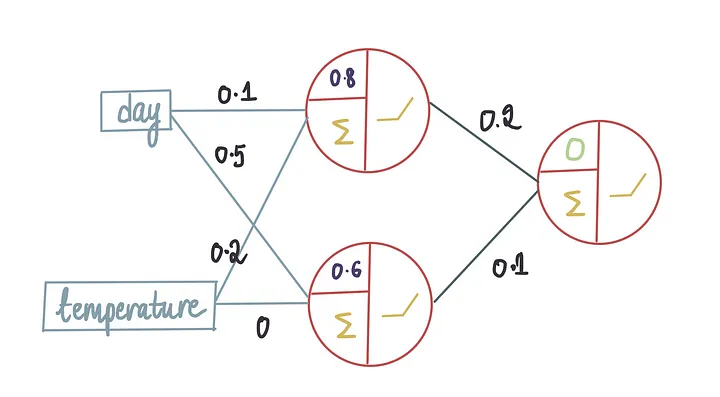
现在，我们需要将所有冰淇淋商店的特征输入以进行收入预测（也就是我们在前一篇文章中学习的前向传播），假设最后一个偏置项为0。让我们将训练数据的10行输入到神经网络中……

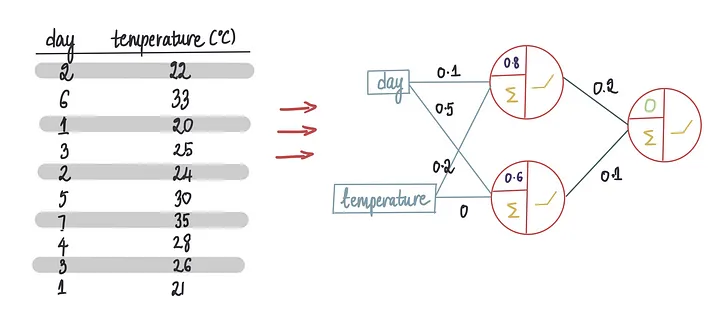
……得到以下预测：

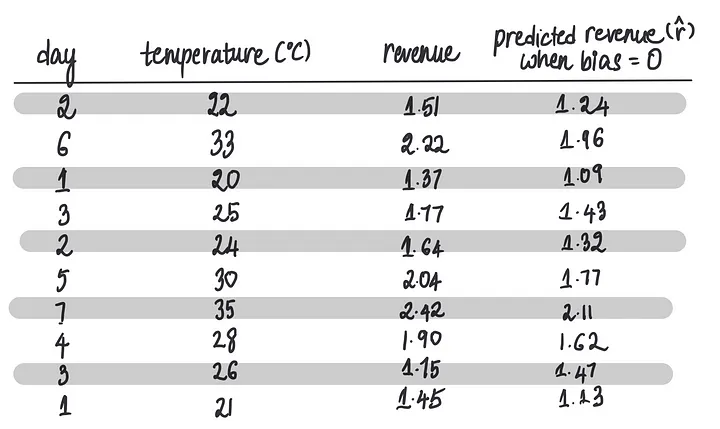
现在我们有了最后一个偏差项等于 0 时的预测，我们就可以将它们与实际收入进行比较。

在上一篇文章中，我们了解到可以使用成本函数来衡量我们预测的准确性，特别是对于我们这种情况下的均方误差（MSE）。

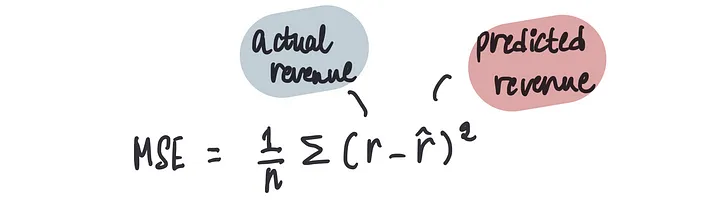
计算此模型在偏置为0时的MSE：

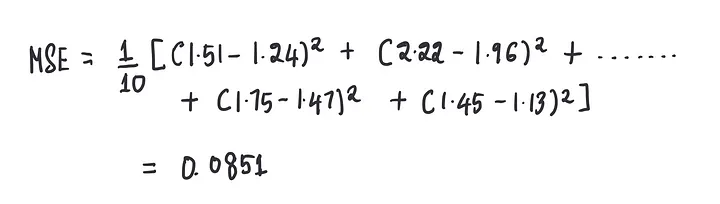
我们也知道任何模型的最终目标都是减少MSE，所以，现在的目标是找到一个最佳的偏置值，来最小化这个MSE。

比较不同偏置值下的MSE值的一种方法是通过暴力破解，并尝试为最后一个偏置项设置不同的值。

例如，让我们对略高于最后一个值 0 的偏差项进行第二次猜测。

接下来让我们尝试偏差 = 0.1。

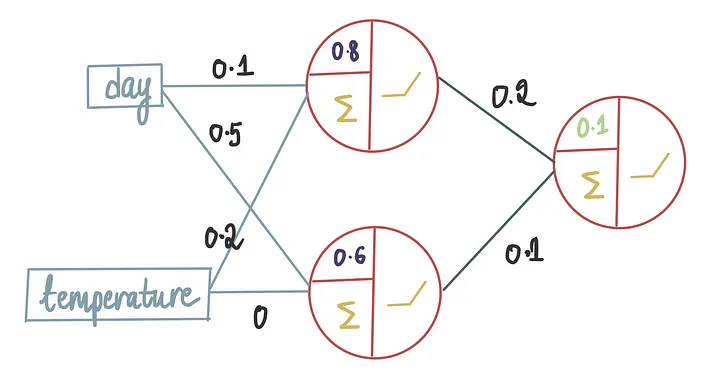
我们将训练数据传递给新的模型，该模型的偏置=0.1……

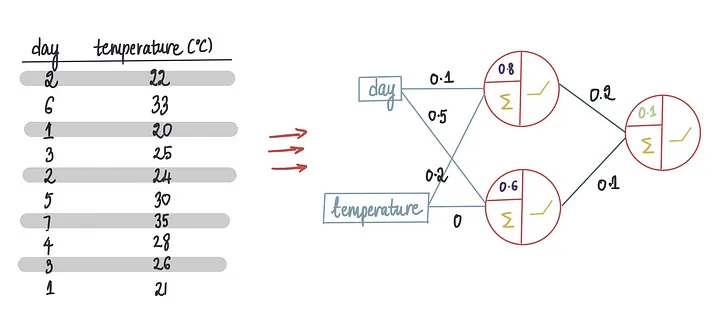
……这将导致这些预测……

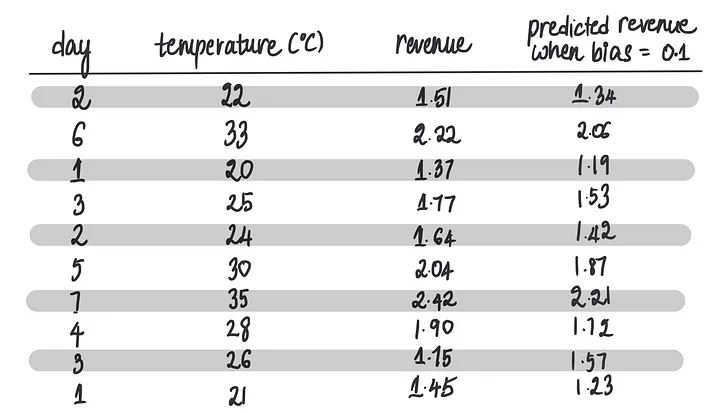
……然后我们使用这些预测来计算MSE：

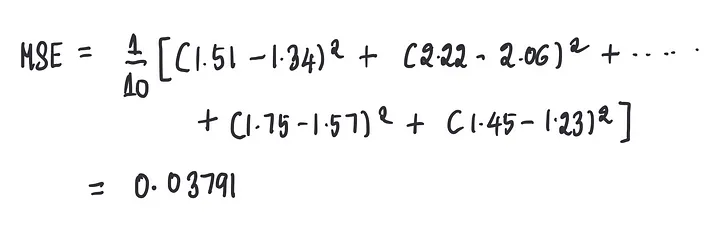
我们可以看到，当偏置设为0.1时，这个模型的MSE（0.03791）比偏置设为0时的MSE（0.08651）略好。

为了更清楚地可视化这一点，让我们将这些值绘制在图表上。

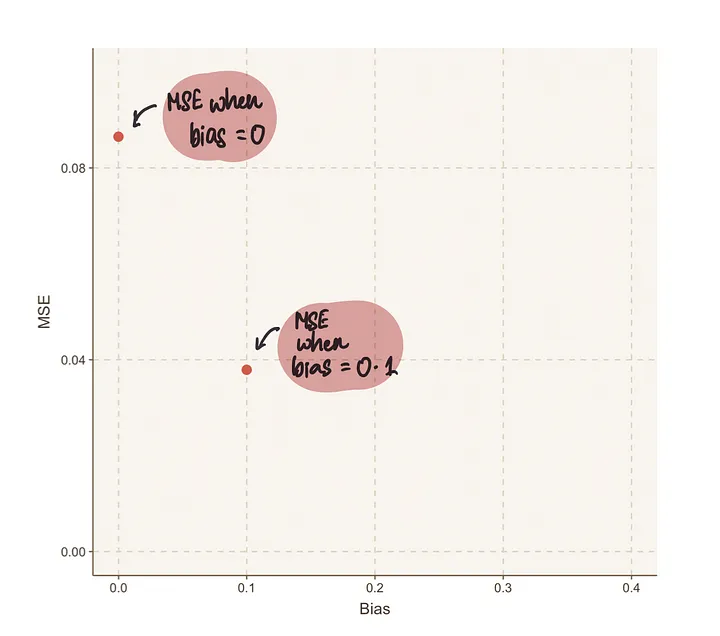
我们可以通过继续猜测值来使用这种暴力破解方法。

假设我们还猜测了另外4个值：偏置=0.2、0.3、0.4和0.5。

我们重复上述相同的过程，生成一个像这样的MSE图表：

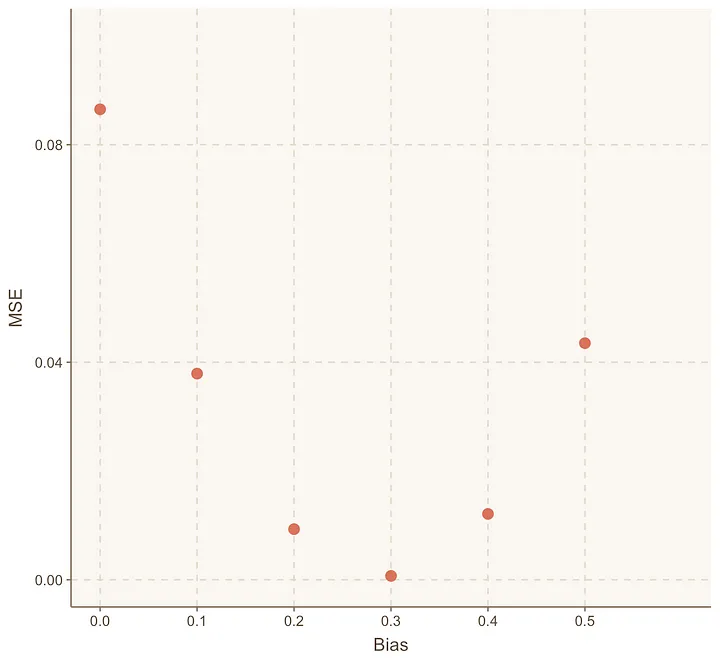
我们注意到，当偏置=0.3时，MSE达到了最低点。

而当偏置=0.4时，MSE又开始增加。

这告诉我们，在偏置=0.3时，MSE达到了最小值。

幸运的是，我们在几次有根据的猜测后就能确定这一点，然后通过进一步的尝试进行确认。

但是，如果最优的MSE值是100，那怎么办呢？在那种情况下，我们可能需要做1000次（100 x 10）猜测才能达到这个值。

因此，这种方法在寻找最优偏置值时并不是非常高效。

此外，我们如何确定具有最低MSE值的偏置就是0.3呢？如果它是0.2998或0.301呢？

所以使用这种方法很难做出精确的猜测。

梯度下降

不过我们有一个更高效的方法来确定最优偏置值。我们将使用一种叫做梯度下降的概念。

简单来说，通过使用梯度下降和导数，我们可以有效地达到任何凸曲线（基本上是一个U形曲线）的最低点。

这在我们当前的情况下是理想的，因为上面的MSE图表类似于U形曲线，我们需要找到MSE最小化的谷底。

梯度下降通过指示每一步的大小和方向来引导我们，以尽快到达曲线的底部。

现在，让我们重新开始使用梯度下降中提出的步骤来寻找最优偏置。

第 1 步：从偏差的随机初始值开始

我们可以从偏置=0开始：

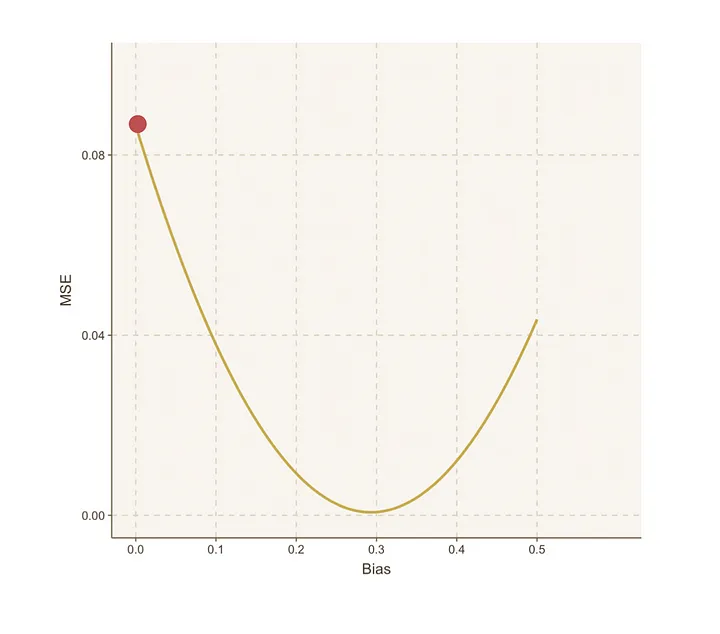
第二步：计算步长

接下来，我们需要确定应该采取的步骤的方向和大小。

这可以通过计算步长来实现，步长是将一个称为学习率的常数值与偏置值处MSE的梯度相乘的结果。

在这种情况下，对于这次迭代，偏置值为0。

注意：学习率是一个用于控制步长的常数。通常，它的值介于0和1之间。

让我们更仔细地检查导数值。我们知道MSE是r_hat的函数，如公式所示：

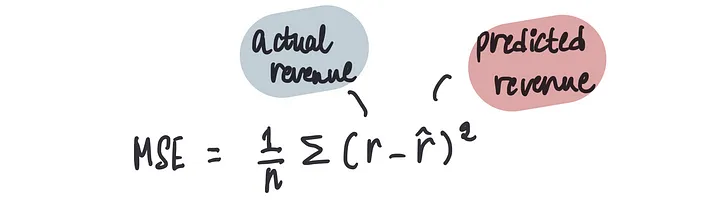
而且我们还知道r_hat是由最后一个神经元中的ReLU函数确定的，因为我们只能通过使用激活函数来获得r_hat：

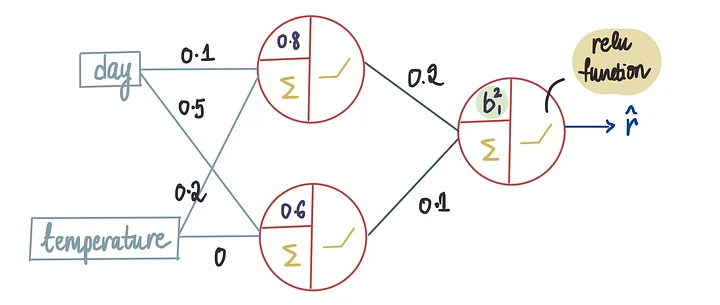
我们知道最后一个神经元中的ReLU函数包含偏置项。

现在，如果我们想要计算MSE关于偏置的导数，我们将使用称为链式法则的东西，这是微积分的一个非常重要的部分，它利用了上述三个关键信息。

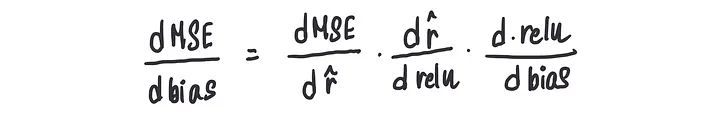
我们需要使用链式法则，因为各个项是相互依赖的，但并不直接依赖。

它被称为链式法则是因为它们都是通过一个链式结构相互连接的。

你可以认为分子和分母相互抵消了。

这就是我们如何计算MSE关于偏置的导数。

我们在当前的偏置值（0）处计算这个导数。

第三步：使用上述步长更新偏置值

**
**

这将为我们提供一个新的偏置值，这个值有可以让我们更接近最优偏置值。

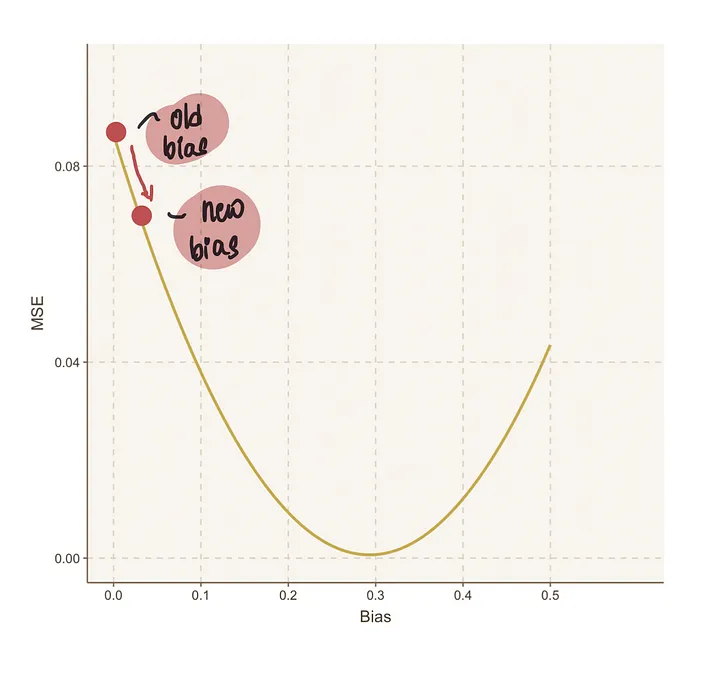
第四步：重复步骤2到3，直到我们达到最优值

我们将继续重复这一步骤的过程

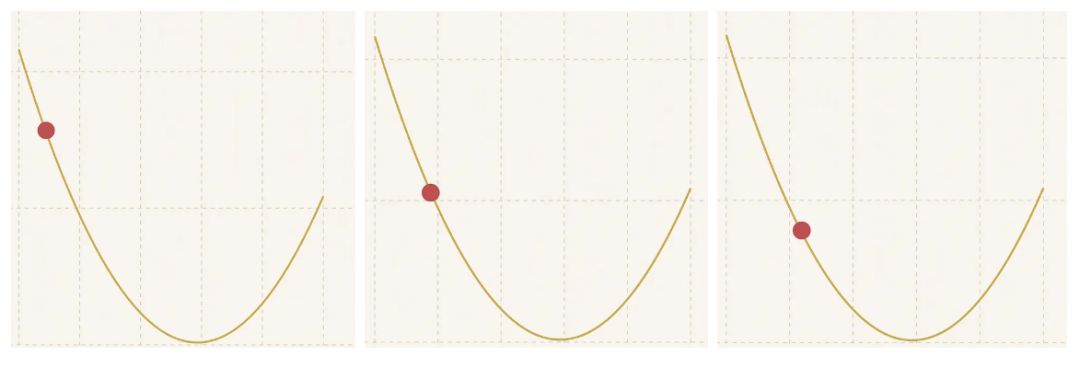
……采取微小的跳跃，随着我们逐渐接近最低点，步长也在缩小……

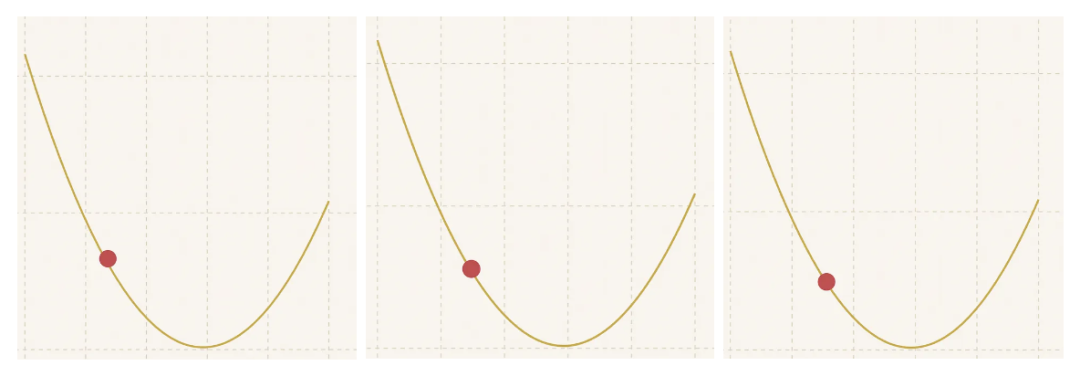
直到最后……

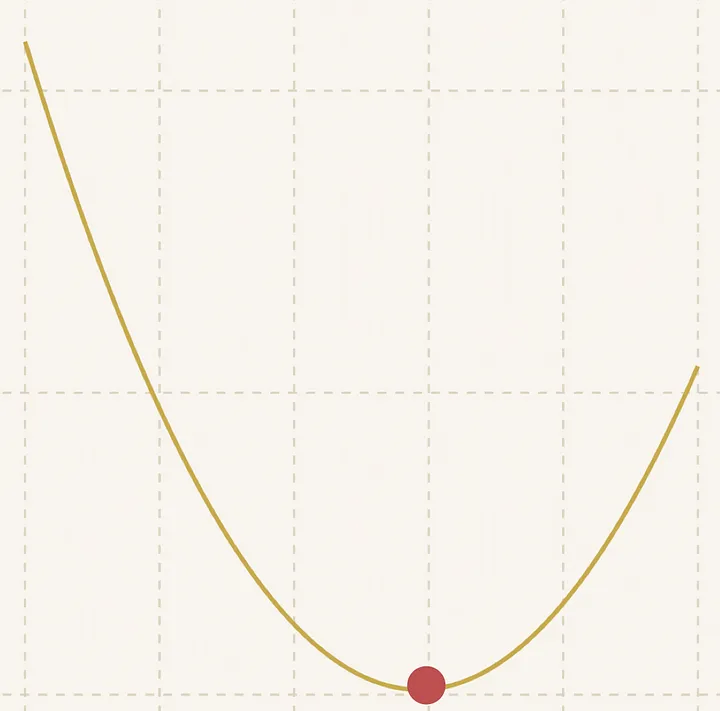
我们达到最优值！

注意：当步长接近0，或者当我们达到算法中设定的最大步数时，我们就得到了最优值。

这就是在假设其他变量的最优值已知的情况下，我们如何找到偏置项的方法。

现在，让我们再进一步，考虑一个场景，其中我们知道除了偏置项和进入最后一个神经元的第二个输入的权重之外的所有最优值。

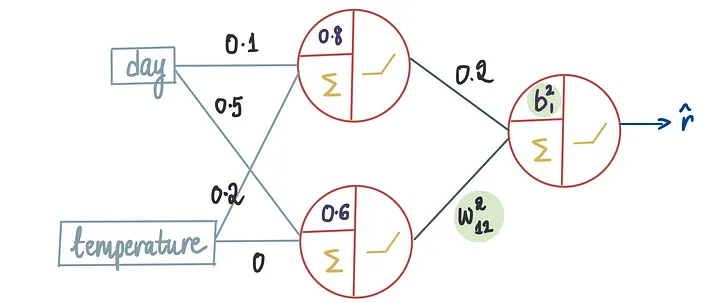
同样，我们需要找到这两个项的最优值，以使MSE最小化。

对于权重和偏置的不同值，我们创建一个MSE图。

这个图将与上面显示的图类似，但将是三维的。

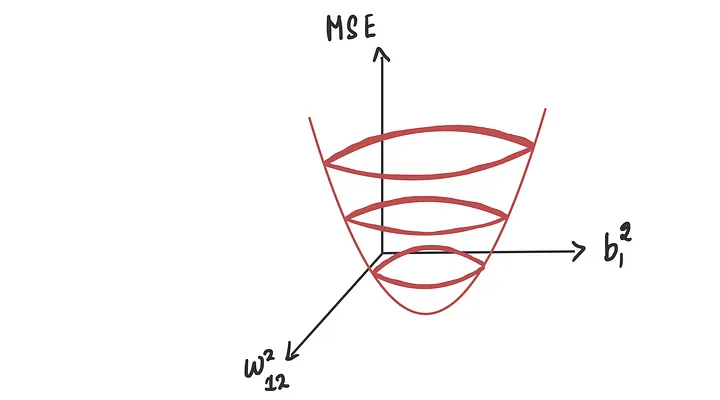
与之前的MSE曲线类似，我们需要找到使MSE最小化的点。

这个点，称为谷底点，将为我们提供偏置和权重项的最优值。

我们可以使用梯度下降法来达到这个最低点。这个过程在这里也基本上是一样的。

步骤1：随机初始化权重和偏置的值

**

---

步骤2：使用偏导数计算步长**

这里有一点小的偏差。

我们不是计算均方误差（MSE）的导数，而是计算所谓的偏导数，并同时更新步长。

这里的“同时”意味着我们需要在当前的权重和偏置值下计算偏梯度的值，并且我们再次使用链式法则：

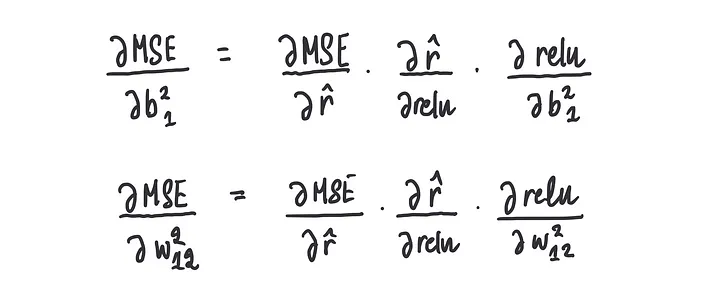
步骤3：同时更新权重和偏置项

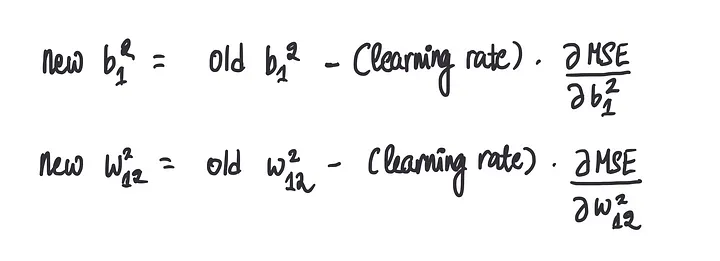
步骤4：重复步骤2-3，直到我们收敛到最优值

**
**
我们可以进一步拓展这个思路。

现在，如果我们想要优化神经网络中的所有9个值，要怎么做呢

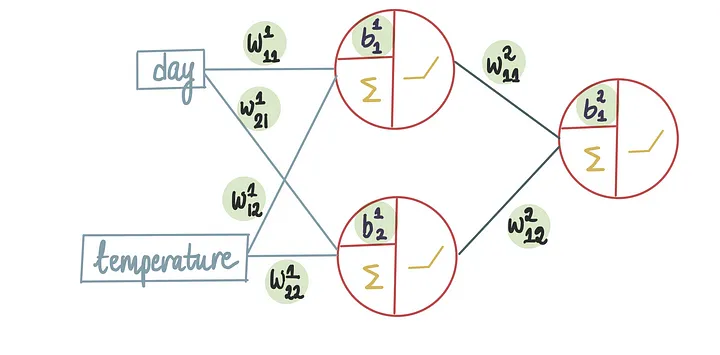
我们面临的是一个涉及九个变量同时优化的复杂问题，需要确保这九个方程在每一次迭代中都能同步更新，以共同寻找函数的最小值。

尽管随着需要同时解决的方程数量的增加，手动进行数学计算变得更加复杂，但概念仍然相同。我们试图逐渐移动到谷底，依靠梯度下降来引导我们。
通过应用上述讨论的方程和优化程序，数据的隐藏模式自然会浮现出来。

这使我们能够找到这些深层模式，而无需任何人为干预。

好的，总结一下，我们现在明白了我们总是想要最小化成本函数（在上面的案例中是MSE），以及如何使用梯度下降来获取使MSE最小化的权重和偏置项的最优值。
我们了解到，通过使用梯度下降，我们可以轻松地遍历一个凸形曲线以到达底部。

幸运的是，在我们的案例研究中，我们有一个看起来很漂亮的凸形曲线。

但是有时我们可能会遇到不产生完美凸形曲线的成本函数，而是产生像这样的东西

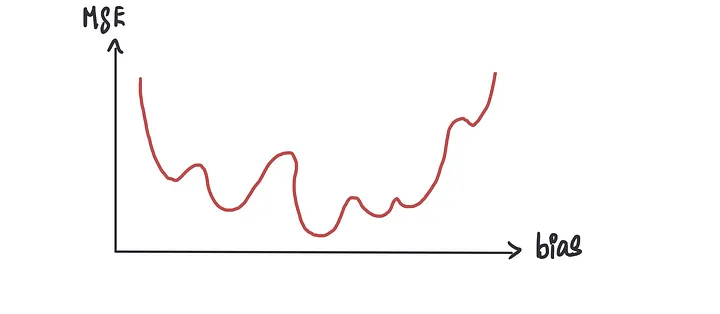
如果我们使用梯度下降法，有时可能会错误地将许多局部最小值（看起来是最低点但实际上并不是）中的一个识别为最低点，而不是全局最小值（实际的最低点）。

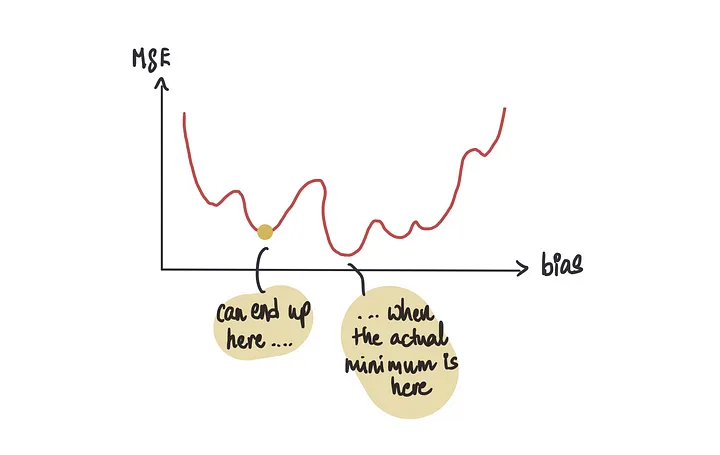
梯度下降法的另一个问题是，随着数据集中数据点数量的增加或项数的增加，执行梯度下降所需的时间也会增加。

这是因为涉及的数学计算变得更加复杂。
在我们的小例子中，我们有10个数据点（这非常不现实，通常我们有数十万个数据点），并且我们试图优化9个参数（这个数字可能非常高，取决于架构的复杂性）。

目前，对于梯度下降的每次迭代，我们使用10个数据点来计算偏导数并更新9个参数值。

这基本上就是是梯度下降在做的事：

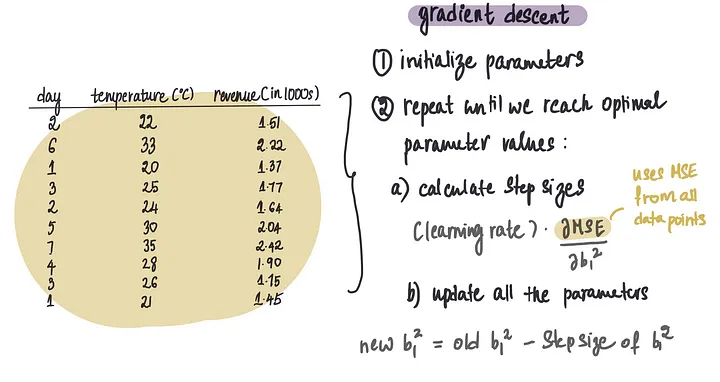
在每次迭代中，我们执行大约90次（910）小的计算，来计算每个单独数据点的MSE的导数。

通常，我们会进行大约1000次这样的迭代，总共需要进行90,000次（901000）计算。
但是，如果我们有10万个数据点而不是只有10个数据点呢？

在这种情况下，我们需要计算所有10万个数据点的MSE，并对90万个（= 9100,000）项取导数。

通常，我们会执行大约1000步梯度下降以达到我们的最优值，这将导致惊人的9亿（900,0001000）次计算。

此外，我们的数据可能会变得更加复杂，数字达到数百万，并且需要优化更多的参数。

这很快就会变得非常具有挑战性。
为了避免这个问题，我们可以利用更快、更强大的替代优化算法。

随机梯度下降

随机梯度下降（SGD）与梯度下降类似，但存在微小的差异。

在梯度下降中，我们在计算了整个包含所有10个值的训练数据集的均方误差（MSE）后更新我们的值。

然而，在SGD中，我们只使用数据集中的一个数据点来计算MSE。
该算法随机选择一个数据点，并使用它来更新参数值，而不是使用整个数据集。

这种方法更加轻便，因此比其全面覆盖的对应方法更快。

小批量梯度下降
这种方法是常规梯度下降和随机梯度下降的结合。

我们不是基于单个数据点或整个数据集来更新值，而是每次迭代处理一批数据点。我们可以选择批次大小为5、10、100、256等。
例如，如果我们的批次大小为4，我们将基于4行数据来计算用于偏导数的MSE。

​

如何学习AI大模型？

作为一名热心肠的互联网老兵，我决定把宝贵的AI知识分享给大家。 至于能学习到多少就看你的学习毅力和能力了 。我已将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

一、全套AGI大模型学习路线

AI大模型时代的学习之旅：从基础到前沿，掌握人工智能的核心技能！

二、640套AI大模型报告合集

这套包含640份报告的合集，涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师，还是对AI大模型感兴趣的爱好者，这套报告合集都将为您提供宝贵的信息和启示。

三、AI大模型经典PDF籍

随着人工智能技术的飞速发展，AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型，如GPT-3、BERT、XLNet等，以其强大的语言理解和生成能力，正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。

四、AI大模型商业化落地方案

作为普通人，入局大模型时代需要持续学习和实践，不断提高自己的技能和认知水平，同时也需要有责任感和伦理意识，为人工智能的健康发展贡献力量。