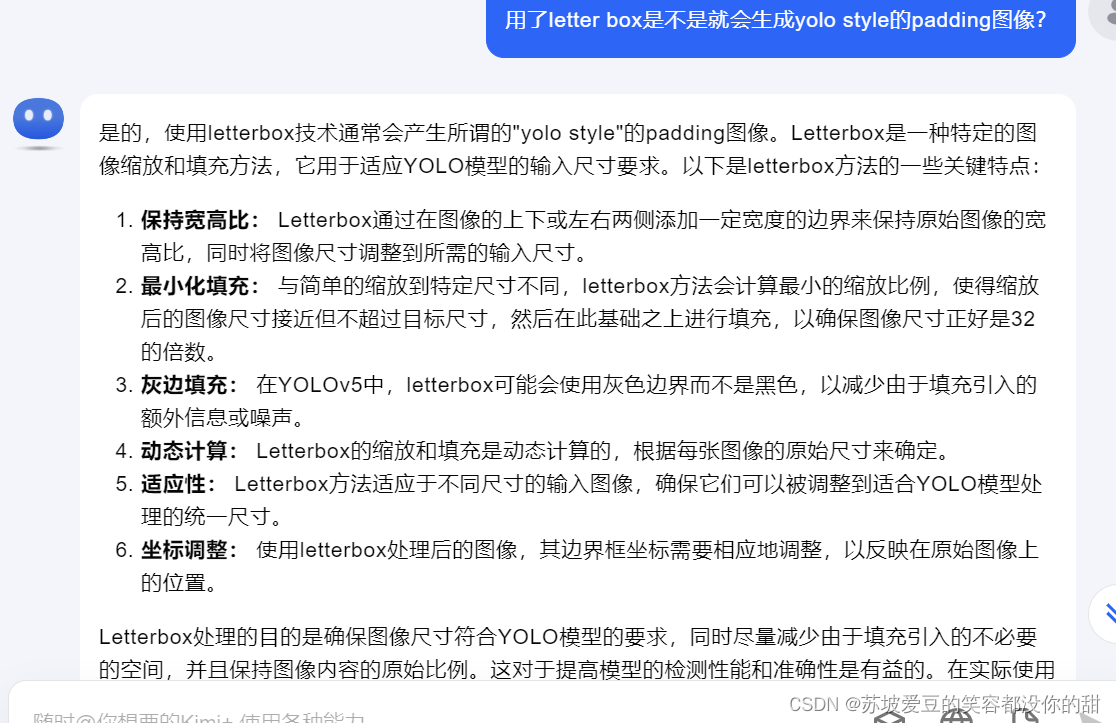
箱形图是什么？

箱形图（也称为箱线图）使用箱体和线条来表示一个或多个组的数值数据分布。箱体的边界表示数据中间50%的范围，中央线标示中位数值。线从每个箱体延伸出来，捕捉其余数据的范围，在线条之外的点表示离群值。箱形图用途很广泛，在六西格玛项目中亦经经常会应用得到。

箱形图显示按月分组的每日下载量

上面的示例箱形图显示了一个虚构的数字应用程序的每日下载量，按月分组。从这个图中可以看到，下载量从一月每天大约75次逐渐增加到八月每天大约95次。十一月和十二月的中位下载量似乎略有下降。点显示了下载量异常的天数：六月有两天和十月有一天的下载量较低。相比于等效的折线图，箱形图提供了一个更清晰的数据总体趋势表示。

什么时候应该使用箱形图？

箱形图用于显示数值数据的分布，特别是当你想要在多个组之间进行比较时。它们提供了一个一目了然的宏观信息，展示了数据组的对称性、偏度、方差和离群值。很容易看到数据的主要部分在哪里，并进行不同组之间的比较。

另一方面，箱形图的简单，也限制了它所能显示的数据密度的能力。使用箱形图时，我们无法观察分布形状的详细信息，例如分布的模态（峰的数量）和偏度。

看看下图两个不同的直方图可以产生一个相同的箱形图。 这两个直方图背后的数据集生成了中间面板中的相同箱形图。

解释箱线图

箱形图的构造基于数据集的四分位数，即将数据集分成相等四部分的值。第一个四分位数（Q1）大于25%的数据且小于其余75%。第二个四分位数（Q2）位于中间，将数据分成两半。Q2也称为中位数。第三个四分位数（Q3）大于75%的数据且小于剩下的25%。在箱线图中，箱体的两端和中央线标示这三个四分位数的位置。

箱线图如何从数据集中得出。 Q3和Q1之间的距离称为四分位距（IQR），在确定从箱体延伸出来的须的长度时起着重要作用。每个须延伸到每个侧翼内距离箱体端点1.5倍IQR以内的最远数据点。任何超过该距离的数据点被视为离群值，并用点标记。还有其他定义须长度的方法，稍后会讨论。

当数据分布对称时，可以预期中位数位于箱体的正中间：Q1和Q2之间的距离应与Q2和Q3之间的距离相同。离群值应均匀分布在箱体的两侧。如果分布偏斜，则中位数不会在箱体中间，而是偏向一侧。你可能还会发现须的长度不平衡，一侧短且无离群值，另一侧有长尾且有更多离群值。

数据形状会影响箱线图的外观。 数据结构示例 箱形图可以从包含数据值和数据组列的表格生成 可视化工具通常能够从一列未汇总的原始数据生成箱形图；箱体端、须和离群值的统计信息在绘图过程中会自动计算。当需要为多个组绘制箱形图时，组通常由第二列表示，如上表所示。

使用箱形图的最佳实践

比较多个组

当需要在组之间进行分布比较时，箱形图效果最佳。它们在数据总结中非常紧凑，通过箱线标记的位置很容易比较组。

当你只有一个组的分布要绘制时，很难证明使用箱形图的合理性。箱形图只提供数据的高层摘要，无法显示数据分布形状的详细信息。只有一个组时，我们可以选择更详细的图表类型，如直方图或密度曲线。

考虑组的顺序

如果绘制箱形图的组没有固有的顺序，则应考虑按顺序排列它们，以突出模式和洞察。一个常见的排序方法是按中位数值排序。

按团队名称和中位数排序的箱形图并排比较

常见的箱形图选项

垂直和水平箱形图

如上文所述，箱形图可以对齐，使得箱体垂直放置（组在水平轴上）或水平放置（组垂直对齐）。当有很多组要绘制或组名较长时，水平排列可能是一种有用的格式。它还允许渲染长类别名称而无需旋转或截断。另一方面，当分组变量基于时间单位时，垂直排列可能是更自然的格式。

箱形图可以水平或垂直排列

可变箱宽和凹槽

某些可视化工具包括选项，将额外的统计信息编码到箱形图中。当收集的数据代表来自更大人群的样本观察时，这很有用。

凹槽用于显示数据代表样本时对中位数最可能的值的预期。当在组之间进行比较时，可以通过凹槽范围是否重叠来判断中位数之间的差异是否具有统计显著性。如果任何凹槽区域重叠，则我们不能说中位数之间的差异具有统计显著性；如果它们没有重叠，那么我们可以有较高的信心认为实际中位数不同。

箱形图中的凹槽表示中位数真值的不确定性。 此图表明，过程B生成的组件具有更好的（更高的）故障时间，但重叠的凹槽表明中位数差异不具有统计显著性。