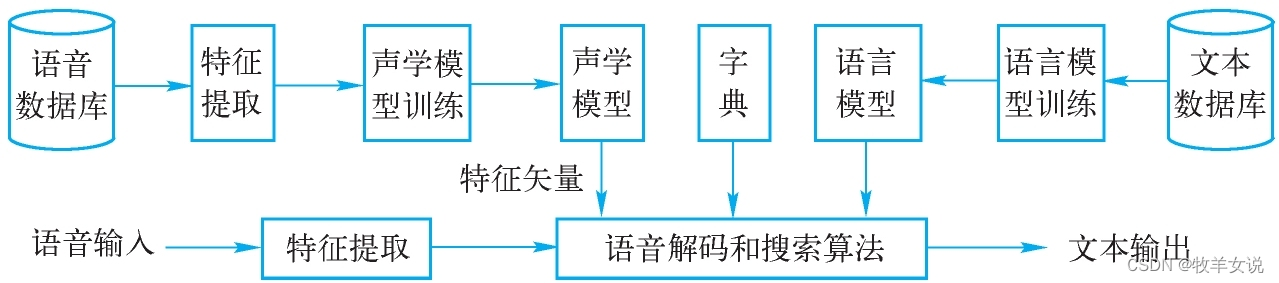
语音识别就是把一段语音信号转换成对应的文本信息,这一过程包括四个大的模块,分别是:特征提取、声学模型、语言模型、字典与解码。
本篇就来梳理一下特征提取模块的实现思路和方法。
常用的语音特征有:
- 梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficients, MFCC)
- 梅尔滤波器组系数(Mel Filter Bank, FBank,也叫log-Mel)
- 线性预测系数(Linear Prediction Coefficient, LPC)
基于深度学习网络的语音识别,目前多采用FBank特征。 获得FBank特征主要包括以下几个步骤:
- 预加重;
- 分帧、加窗;
- 快速傅里叶变换,计算功率谱;
- Mel滤波器组;
- 取对数,得到FBank。
1. 预加重(Pre-Emphasis)
在音频录制过程中,高频信号更容易衰减,高频成分的丢失,可能导致音素的共振峰不明显,使得声学模型对这些音素的建模能力不强。预加重是个一阶高通滤波器,可以提高信号高频部分的能量。
预加重的实现方法:给定时域输入信号x,预加重之后的信号y为:y(t)=x(t)−αx(t−1),其中0.9≤α≤1.0。经过预加重之后的频谱图和原始的频谱图的比较如下图所示,其中,左侧为原始频谱图,右侧为预加重处理之后的频谱图。
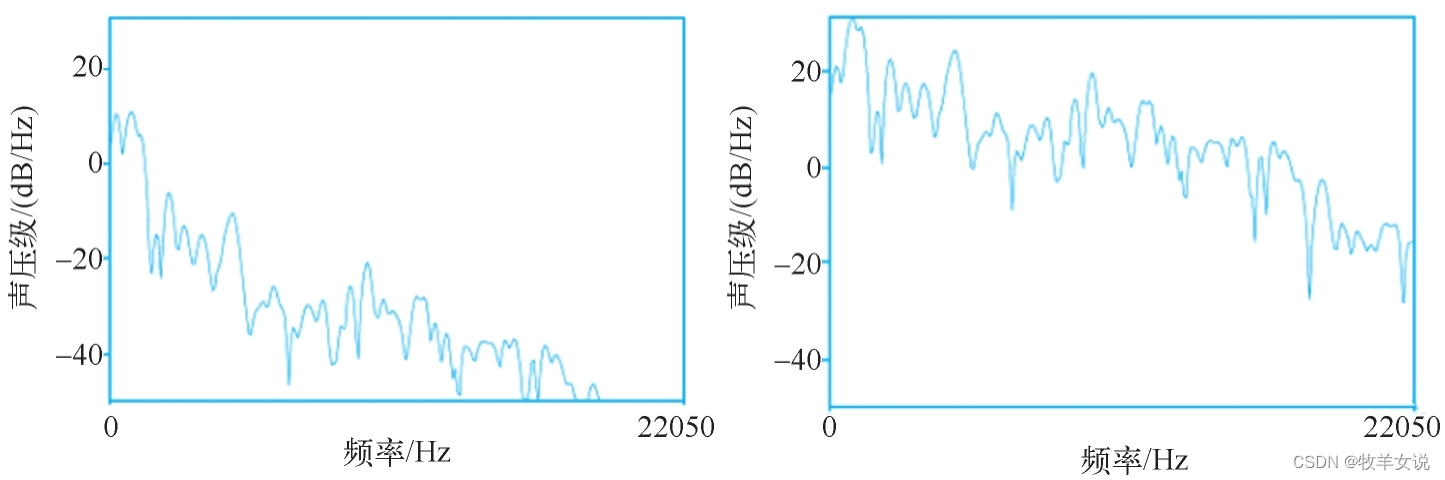
2. 分帧、加窗
语音信号是一个时变的、非稳态的信号,但在短时间范围内可以认为是时不变的、稳态的。这个短时间的长度一般取10~30ms,可在这个时间范围内进行语音信号处理。这就是分帧。
分帧一般采用交叠分段的方法,这是为了使帧与帧之间平滑过渡,保持其连续性。前一帧和后一帧的交叠部分称为帧移,帧移与帧长的比值一般为0~1/2。分帧如下图所示:
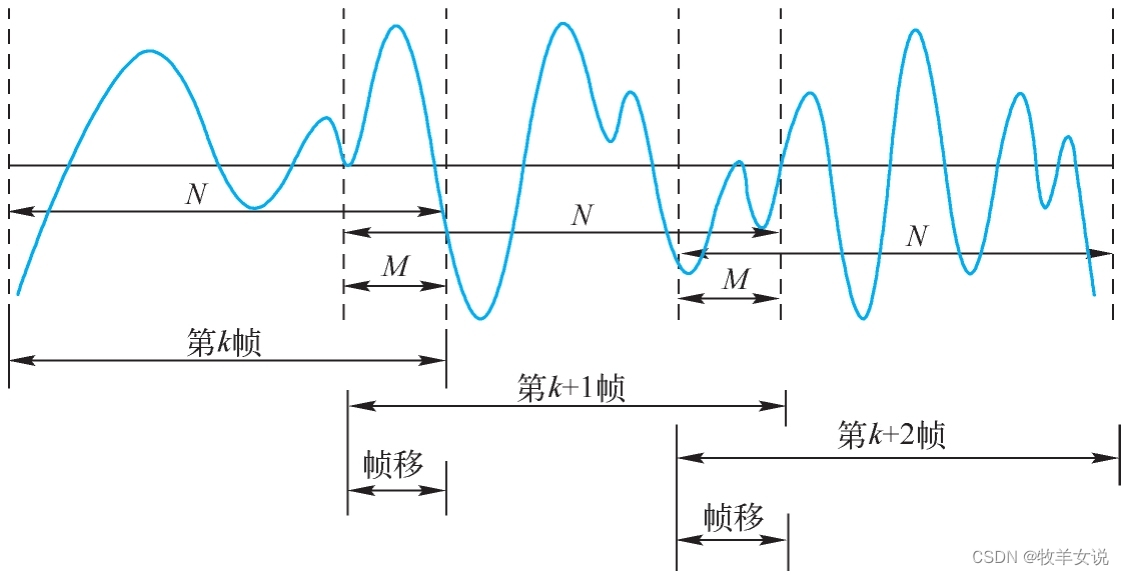
分帧之后,需要使用有限长度窗口进行加权处理,也就是加窗,即sw(n) = s(n) * w(n)。那么,为什么要加窗呢?这是因为后面要对信号进行快速傅里叶变换(FFT)。FFT处理的要求是,信号要么从-∞到+∞,要么为周期信号。由于语音信号只能是有限长度信号,并且分帧后的信号是非周期的,进行FFT处理时会存在频率泄露的问题。为了尽可能地减小频率泄露,就需要对信号进行加窗处理。那么,窗函数的选择就需要满足:(1) 窗函数频谱主瓣宽度尽量窄,以得到较高的频率分辨能力;(2) 窗函数旁瓣衰减尽量大,以减少泄露。
下图显示了加窗和不加窗的FFT变换对比:
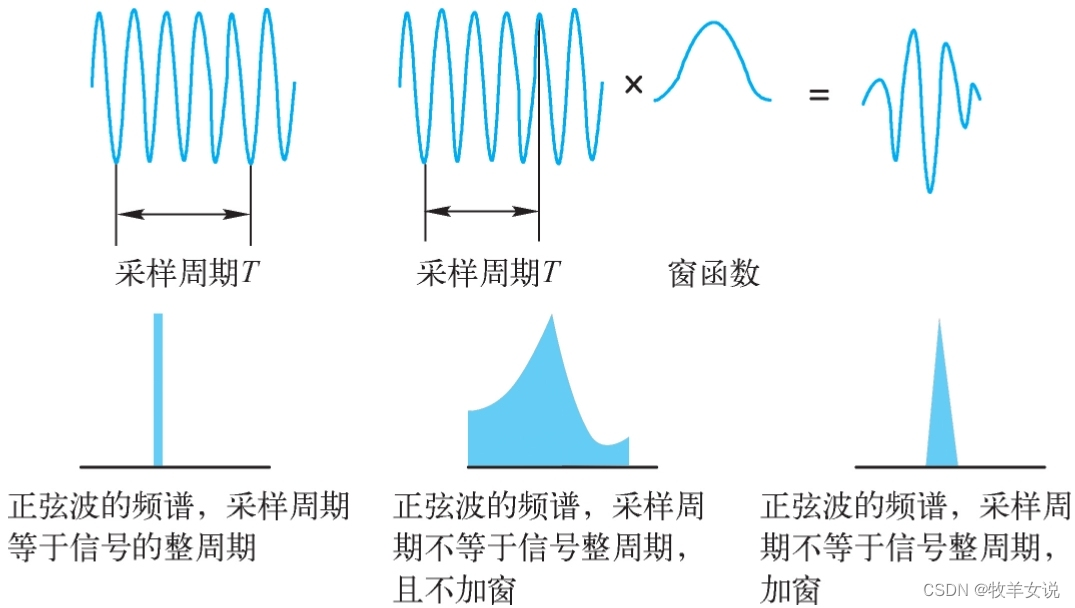
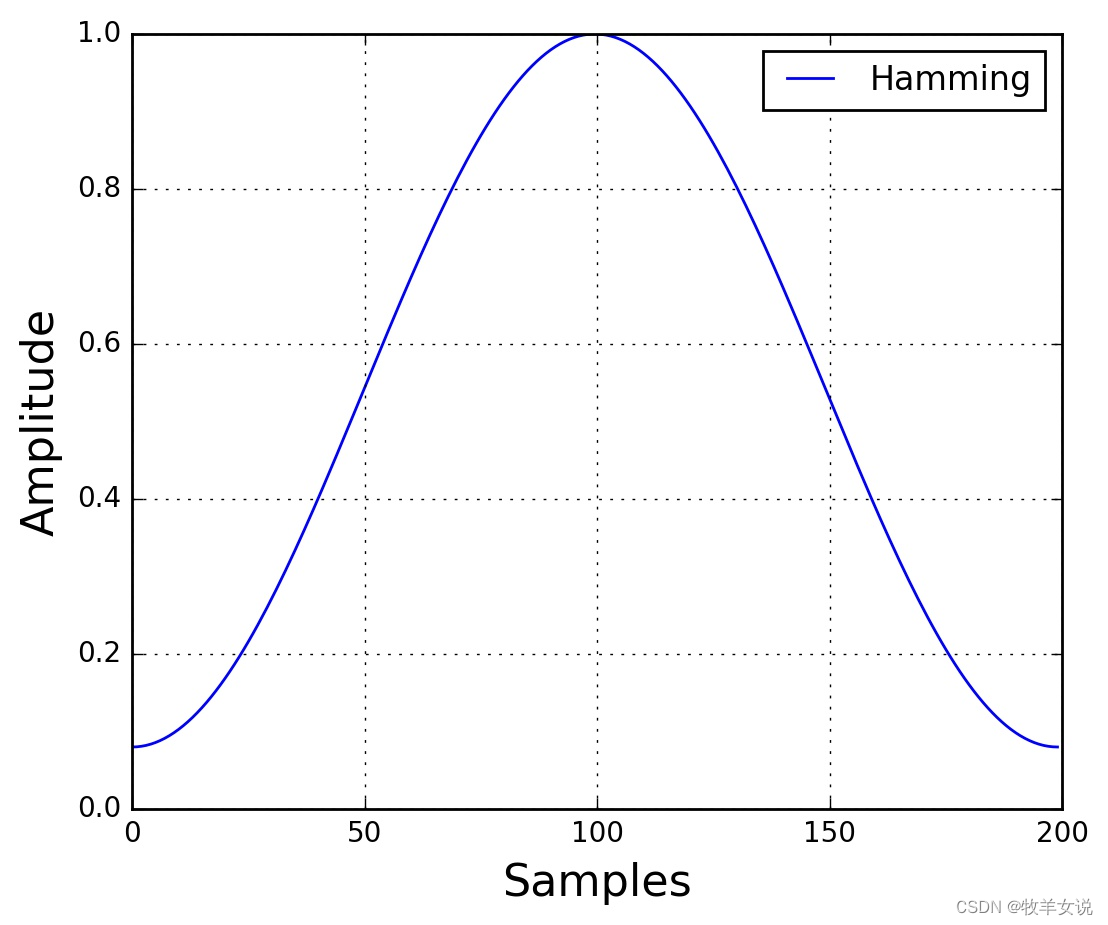
常用的加窗函数有汉明窗(Hamming)、汉宁窗(Hanning)等。其中,汉明窗的窗函数表达式为:
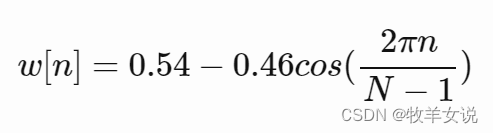
其中,0≤n≤N−1,N为窗口长度。窗口图形绘制如下:
3. 短时快速傅里叶变换(STFT),计算功率谱
对于每一帧加窗信号,进行N点FFT变换,也称为短时傅里叶变换(STFT),N通常取256或512。然后,计算能量谱:
![]()
4. Mel滤波器组
人耳对不同频率的声音有不同的感知能力,通常情况下,人耳对低频的感知辨识力比高频更好,为了模拟人耳对不同频率的非线性感知能力,引入了Mel频率。赫兹频率(f)与Mel频率(m)之间的转换关系如下:
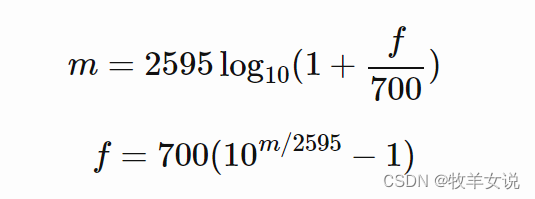
该步是通过定义M个三角滤波器组,对上一步得到的功率谱进行滤波。M的取值范围一般在22~40,标准值为26,这里取40。滤波器组中的每个滤波器都是三角形的,中心频率为f(m),该处响应为1,中心频率两边线性减小到0。各f(m)之间的间隔随着m值的增大而变宽,如下图所示:
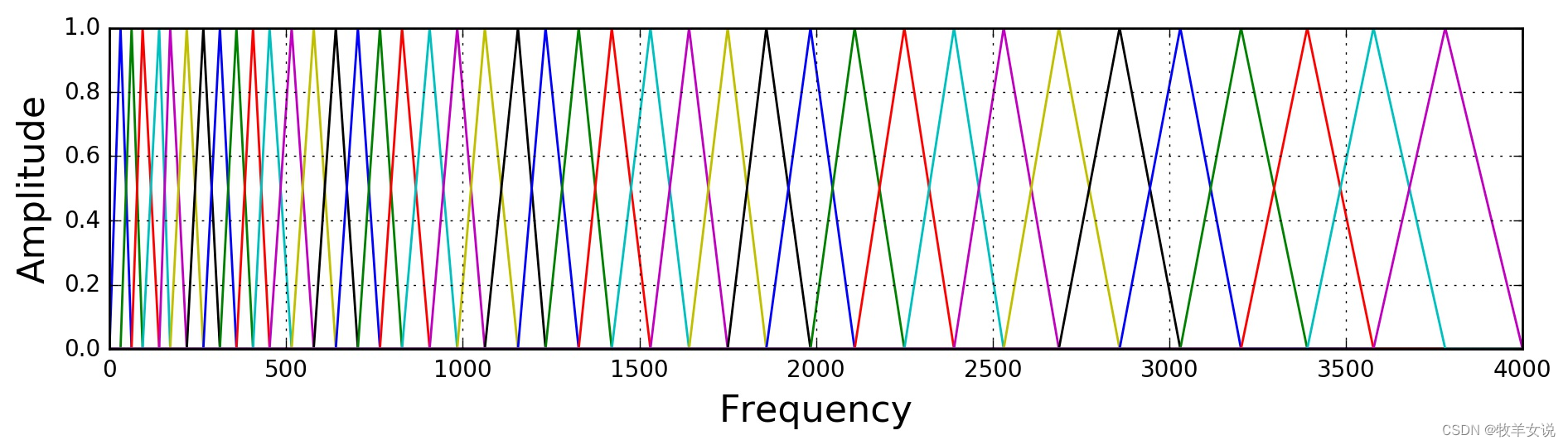
三角滤波器的定义如下:
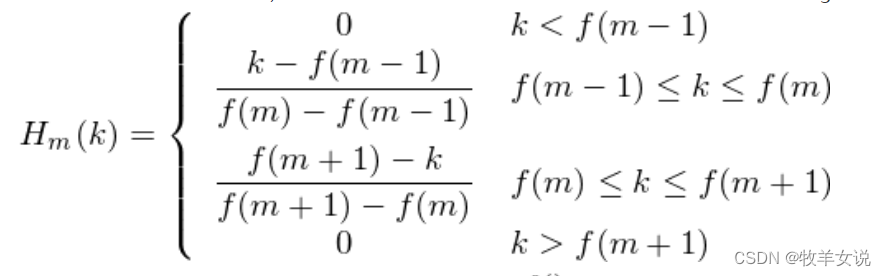
f(m)是在Mel尺度上转换回赫兹频率的位置,由于滤波器最终对第3步计算出来的功率谱进行滤波,因此,在实现中,可以将滤波器位置转换成FFT bin所在的位置来计算。为了说明这一点,用一段代码来描述这个过程:
low_freq_mel = 0
high_freq_mel = (2595 * numpy.log10(1 + (sample_rate / 2) / 700)) # Convert Hz to Mel
mel_points = numpy.linspace(low_freq_mel, high_freq_mel, nfilt + 2) # Equally spaced in Mel scale,在Mel频率范围内均匀创建nfilt+2也就是40个点
hz_points = (700 * (10**(mel_points / 2595) - 1)) # Convert Mel to Hz,将42个点的Mel points转回赫兹频率
bin = numpy.floor((NFFT + 1) * hz_points / sample_rate) # 将hz_points转换到FFT bin
fbank = numpy.zeros((nfilt, int(numpy.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
f_m_minus = int(bin[m - 1]) # left
f_m = int(bin[m]) # center
f_m_plus = int(bin[m + 1]) # right
for k in range(f_m_minus, f_m):
fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1]) # 三角滤波器左侧
for k in range(f_m, f_m_plus):
fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m]) # 三角滤波器右侧
filter_banks = numpy.dot(pow_frames, fbank.T) # pow_frames即当前帧的功率谱
filter_banks = numpy.where(filter_banks == 0, numpy.finfo(float).eps, filter_banks) # Numerical Stability
filter_banks = 20 * numpy.log10(filter_banks) # dB,进行对数计算,得到最终的FBank特征5. 取对数,得到FBank
这一步较简单,在上一步的Python代码中,对三角滤波器组的输出取对数,得到最终的FBank特征。不再赘述。
6. 均值归一化(Mean Normalization)
为了平衡频谱并提高信噪比,可以通过减去(所有帧的)系数平均值的方式来进行归一化。
filter_banks -= (numpy.mean(filter_banks, axis=0) + 1e-8)7. MFCC特征
由于许多ASR系统使用MFCC特征,这里做一个补充说明。
由于FBank系数存在高度相关性,在一些机器学习系统(如之前流行的GMMs-HMMs)中会存在问题,因此,如果对Fbank进行DCT变换来对FBank系数进行去相关,则可以得到MFCC(Mel-Frequency Cepstral Coefficients)。MFCC是FBank的一种压缩表示。在ASR系统中,一般会保留前2~13个系数,其他的则被丢弃。被丢弃的这些系数表示filter bank的快速变化,这些精细的细节对某些ASR系统是没有贡献的。
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1 : (num_ceps + 1)] # num_ceps = 2 - 13还可以对MFCC应用正弦提升来改善ASR在噪声信号下的识别能力:
(nframes, ncoeff) = mfcc.shape
n = numpy.arange(ncoeff)
lift = 1 + (cep_lifter / 2) * numpy.sin(numpy.pi * n / cep_lifter)
mfcc *= lift MFCC也可以应用均值归一化。
参考资料:
Practical Cryptography
Speech Processing for Machine Learning: Filter banks, Mel-Frequency Cepstral Coefficients (MFCCs) and What’s In-Between | Haytham Fayek
《人工智能技术》,郑孝宗主编