基于蚁群算法的XX市旅游景点线路优化系统
(一)客户需求:
①考虑旅游景点的空间分布、游客偏好等因素,实现了旅游线路的智能规划
②游客选择一景点出发经过所要游览的所有景点只一次,最后回到出发点的前提下,要求所走路程最少。
③界面:展示路径,有景点显示,描述一下路径规划
(二)景点数据:
关林(关羽之墓) 112.48,34.61
洛邑古城 112.49,34.68
应天门 116.35,39.88
隋唐遗址植物园 112.45,34.64
白马寺 112.61,34.72
王城公园 112.42,34.67
龙门石窟 112.48,34.56
(三) 蚁群算法
蚁群算法是一种模拟蚁群觅食行为的优化算法,通过模拟蚂蚁在寻找食物时的行为来解决优化问题。
蚁群算法的基本原理是,蚂蚁会通过释放信息素来与其他蚂蚁进行信息交流。在寻找食物的过程中,当一只蚂蚁找到了食物后,会回到巢穴并释放一种称为信息素的化学物质。而其他蚂蚁在移动时会通过感知到这些信息素的浓度来判断哪条路径是更适合寻找食物的。随着时间的推移,蚂蚁会逐渐增加对路径上信息素的释放,从而引导其他蚂蚁选择更短路径。
蚁群算法的优点是能够在复杂的问题中找到较好的解决方案,并且具有较好的鲁棒性和适应性。它的应用领域广泛,包括路线规划、资源分配、组合优化等。
蚁群算法的步骤如下:
- 初始化蚂蚁的位置和信息素浓度。
- 蚂蚁按照一定的规则选择下一个移动的位置。
- 蚂蚁在移动过程中更新信息素浓度。
- 重复步骤2和3,直到找到满意的解决方案或达到迭代次数。
- 通过更新信息素浓度来优化路径选择的过程。
蚁群算法的关键在于信息素的更新和蚂蚁移动规则的设计。合适的信息素更新策略可以增强蚂蚁选择更好路径的能力,而适当的蚂蚁移动规则可以使蚂蚁能够在搜索空间中进行探索和利用的平衡。
代码实现
主函数
clc
close all
clear all
%%
namelist={
'关林(关羽之墓)'
'洛邑古城'
'应天门'
'隋唐遗址植物园'
'白马寺'
'王城公园'
'龙门石窟'};
pos=[112.48,34.61
112.49,34.68
112.467302,34.682326
112.45,34.64
112.61,34.72
112.42,34.67
112.48,34.56];
%%
s="请输入起点:\n 1 关林(关羽之墓)\n 2 洛邑古城\n 3 应天门\n 4 隋唐遗址植物园\n 5 白马寺\n 6 王城公园\n 7 龙门石窟\n";
startid=input(s);
fprintf('已选择起点: %s',namelist{startid})
N=numel(pos)/2;
figure
geoscatter(pos(:,2),pos(:,1),200,'gp','filled')
hold on
for n=1:N
text(pos(n,2)+0.005,pos(n,1),namelist{n})
end
%% 计算距离矩阵
D=zeros(N);
for i=1:N
for j=i+1:N
D(i,j)=SphereDist([pos(i,2),pos(i,1)],[pos(j,2),pos(j,1)]);
D(j,i)=D(i,j);
end
end
route=myACO(D,startid);
lat = [pos(route,2)' pos(startid,2)'];
lon = [pos(route,1)' pos(startid,1)'];
geoplot(lat,lon,"--b","LineWidth",2)
text(pos(startid,2)-0.005,pos(startid,1),'起点')
geoscatter(pos(startid,2),pos(startid,1),150,'ro','filled')
蚁群算法
function bestroute=myACO(D,startid)
n=size(D,1);
%% 初始化参数
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 200; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%% 迭代寻找最佳路径
while iter <= iter_max
% 随机产生各个蚂蚁的起点城市
start = startid*ones(m,1);
% for i = 1:m
% temp = randperm(n);
% start(i) = temp(1);
% end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
iter = iter + 1;
Table = zeros(m,n);
end
bestroute=Route_best(end,:);
结果演示
脚本版:
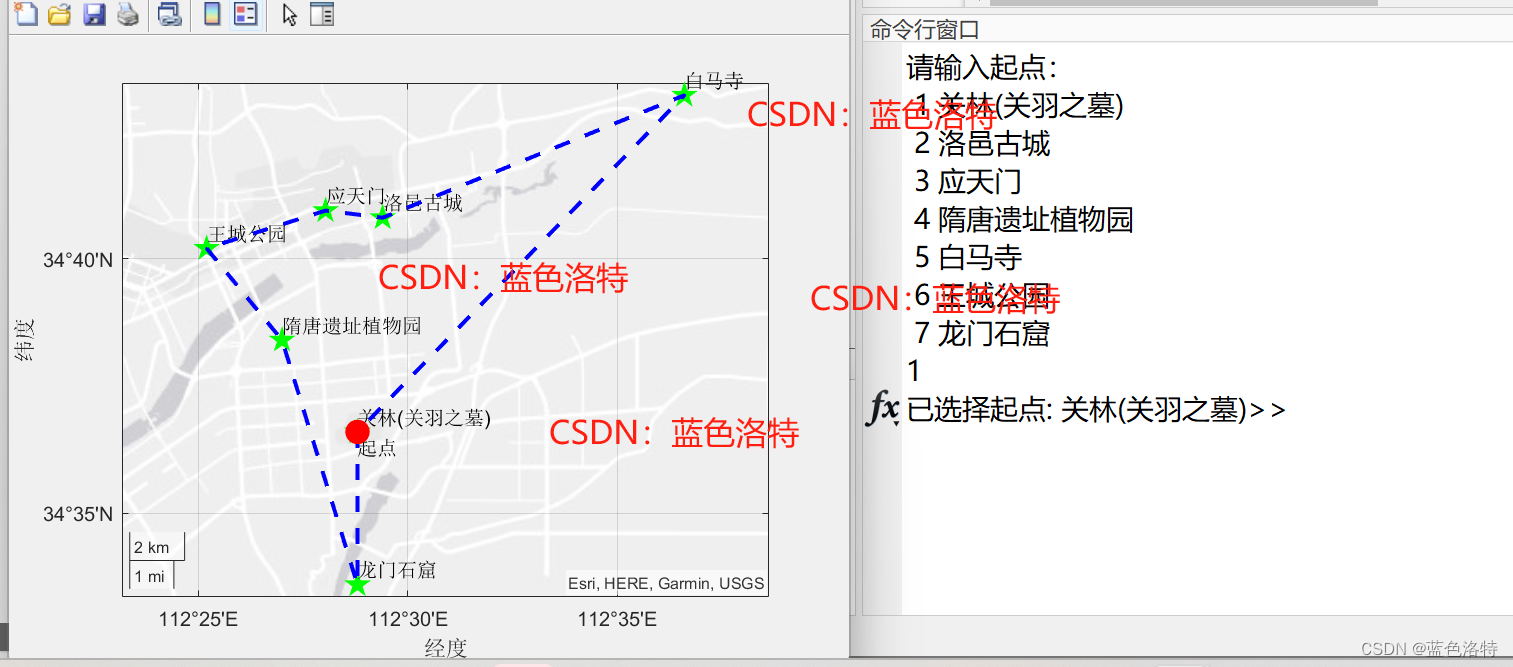
GUI版本:

(五)完整项目分享
提供完整项目分享和项目定制,欢迎咨询