降维算法是一类数据处理技术,主要用于将高维数据映射到低维空间中,从而减少数据的维度。降维不仅可以减少计算复杂度,提高算法性能,还可以帮助数据可视化。常见的降维算法包括主成分分析(PCA)、线性判别分析(LDA)、多维缩放(MDS)、独立成分分析(ICA)、t-分布邻域嵌入(t-SNE)等。
主成分分析(PCA)
主成分(Principal Components)是主成分分析(PCA)中用于减少数据维度的新变量。这些新变量是通过将原始变量线性组合得到的,它们按数据中的方差大小排序。主成分的主要目的是在保持数据主要信息的同时,尽量减少数据的维度。
主成分的定义和性质
-
方差最大化:第一主成分(PC1)是原始数据线性组合后方差最大的方向。第二主成分(PC2)是在正交于第一主成分的方向上方差最大的方向,以此类推。
-
正交性:所有主成分之间都是正交的,即彼此独立不相关。这保证了主成分可以有效地表示原始数据的变化。
-
降维效果:通过选取前几个主成分,可以在很大程度上保留原始数据的变异性,从而实现数据的降维。
PCA的基本步骤
-
标准化数据:如果原始数据的量纲不同,首先需要标准化数据。
-
计算协方差矩阵:计算数据的协方差矩阵,以描述变量之间的关系。
-
特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量。
-
选择主成分:选择特征值最大的几个特征向量作为主成分,这些特征向量是新的坐标系的轴。
应用场景:
-
数据预处理:降维减少数据冗余。
-
数据可视化:高维数据的二维或三维可视化。
Python可视化实例:
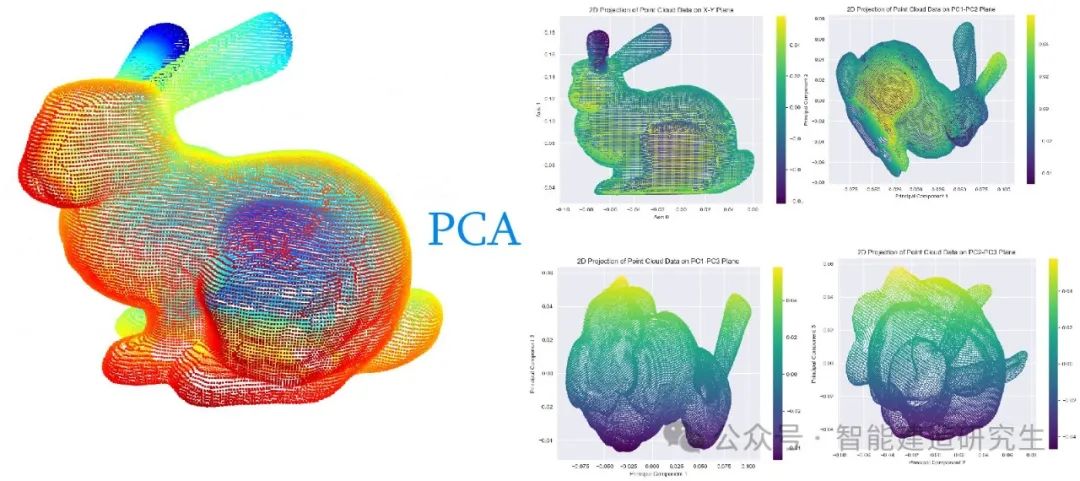
我们使用的Stanford Bunny 数据集是一个经典的三维点云数据集,由斯坦福大学计算机图形实验室在1994年发布。这个数据集包含了一个陶瓷兔子的三维扫描数据,广泛用于计算机图形学、计算机视觉、3D建模和点云处理等领域的研究和教学。我们将三维点云数据经过PCA处理后得到其在不同主成分的二维投影。
import os
import urllib.request
import tarfile
import numpy as np
import open3d as o3d
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
# 下载并解压Stanford Bunny数据集
url = "http://graphics.stanford.edu/pub/3Dscanrep/bunny.tar.gz"
download_path = "bunny.tar.gz"
extract_folder = "bunny"
# 下载数据集
if not os.path.exists(download_path):
print("正在下载数据...")
urllib.request.urlretrieve(url, download_path)
print("下载完成。")
# 解压数据集
if not os.path.exists(extract_folder):
print("正在解压数据...")
with tarfile.open(download_path, "r:gz") as tar:
tar.extractall(path=extract_folder)
print("解压完成。")
# 加载点云数据
# 解压后的路径
ply_path = os.path.join(extract_folder, "bunny", "reconstruction", "bun_zipper.ply")
# 使用open3d读取点云数据
pcd = o3d.io.read_point_cloud(ply_path)
points = np.asarray(pcd.points)
# 打印数据形状
print("点云数据形状: ", points.shape)
# 使用PCA进行降维
pca = PCA(n_components=3)
points_pca = pca.fit_transform(points)
# 打印主成分方差解释比例
print("主成分方差解释比例: ", pca.explained_variance_ratio_)
# 使用open3d进行三维可视化
o3d.visualization.draw_geometries([pcd], window_name='Original Point Cloud', width=800, height=600)
# 使用投影到不同主成分平面进行二维可视化
def plot_projection(points, axes, title_suffix):
plt.figure(figsize=(8, 6))
plt.scatter(points[:, axes[0]], points[:, axes[1]], c=points[:, 2], cmap='viridis', s=1)
plt.colorbar()
plt.xlabel(f'Principal Component {axes[0] + 1}')
plt.ylabel(f'Principal Component {axes[1] + 1}')
plt.title(f'2D Projection of Point Cloud Data on {title_suffix}')
plt.show()
# 投影到不同主成分平面
# 投影到第一主成分和第二主成分平面
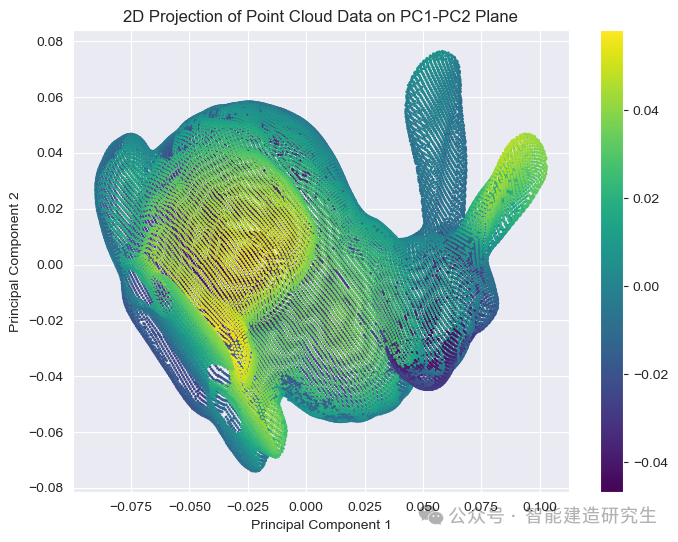
plot_projection(points_pca, [0, 1], "PC1-PC2 Plane")
# 投影到第二主成分和第三主成分平面
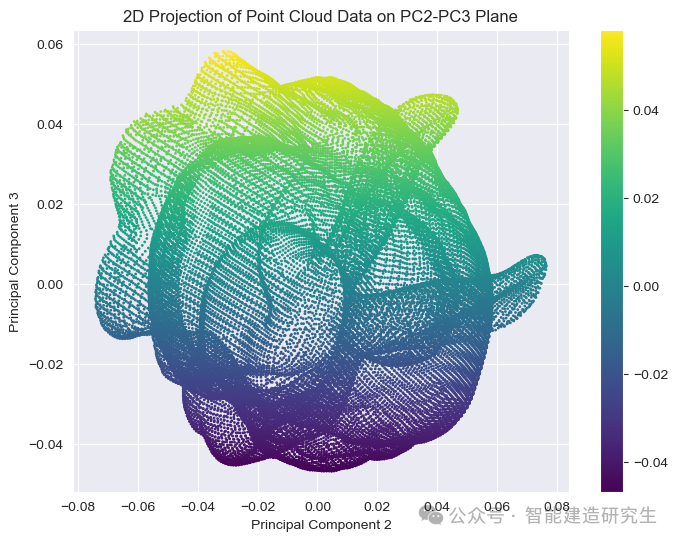
plot_projection(points_pca, [1, 2], "PC2-PC3 Plane")
# 投影到第一主成分和第三主成分平面
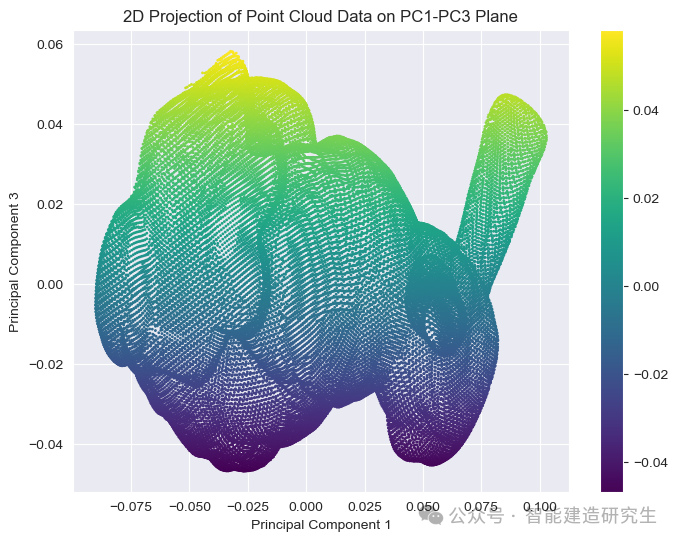
plot_projection(points_pca, [0, 2], "PC1-PC3 Plane")
'''
点云数据形状: (35947, 3)
'''
原始三维点云:
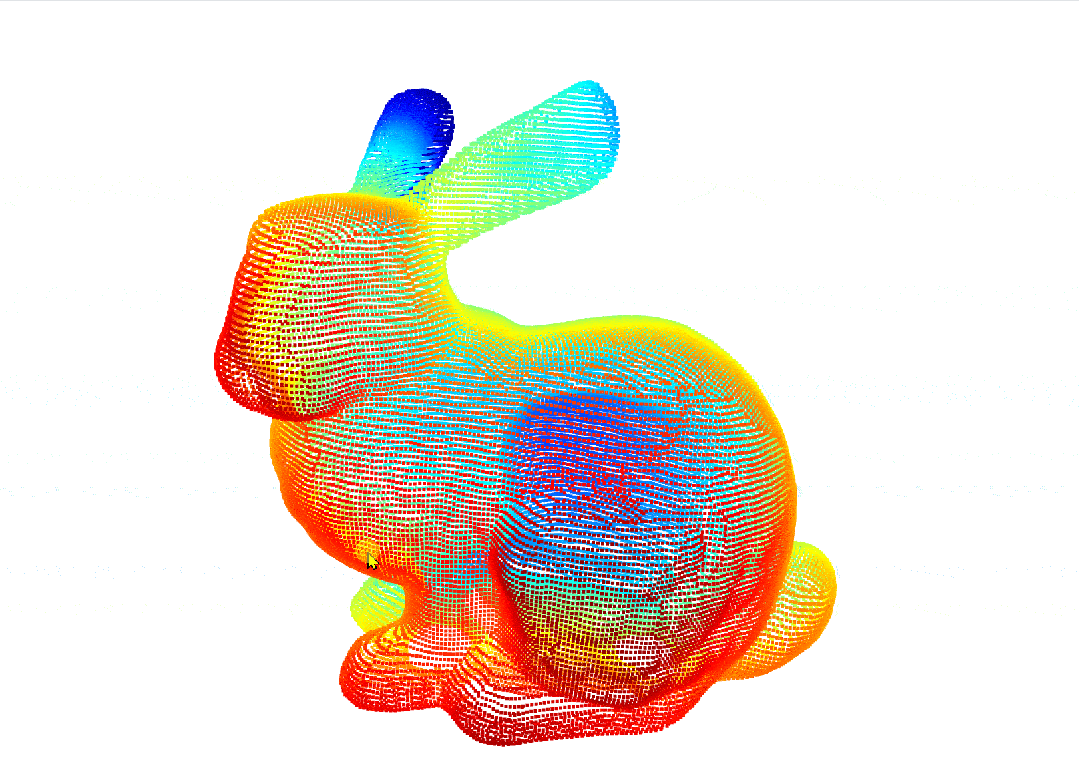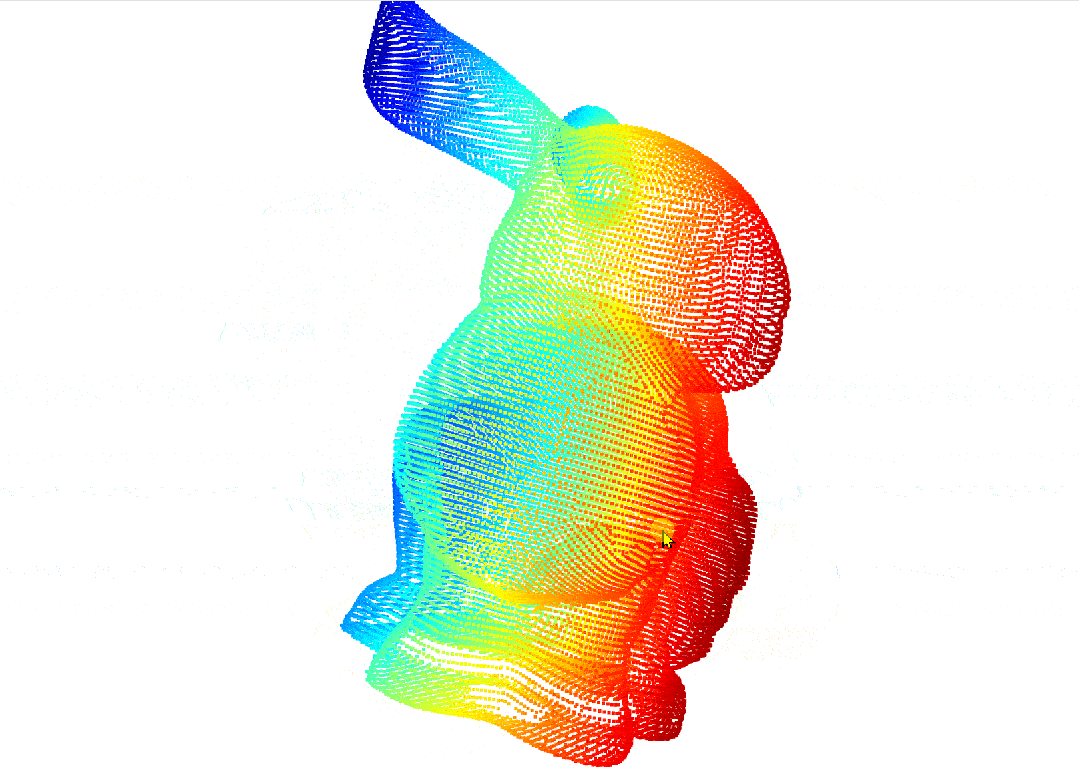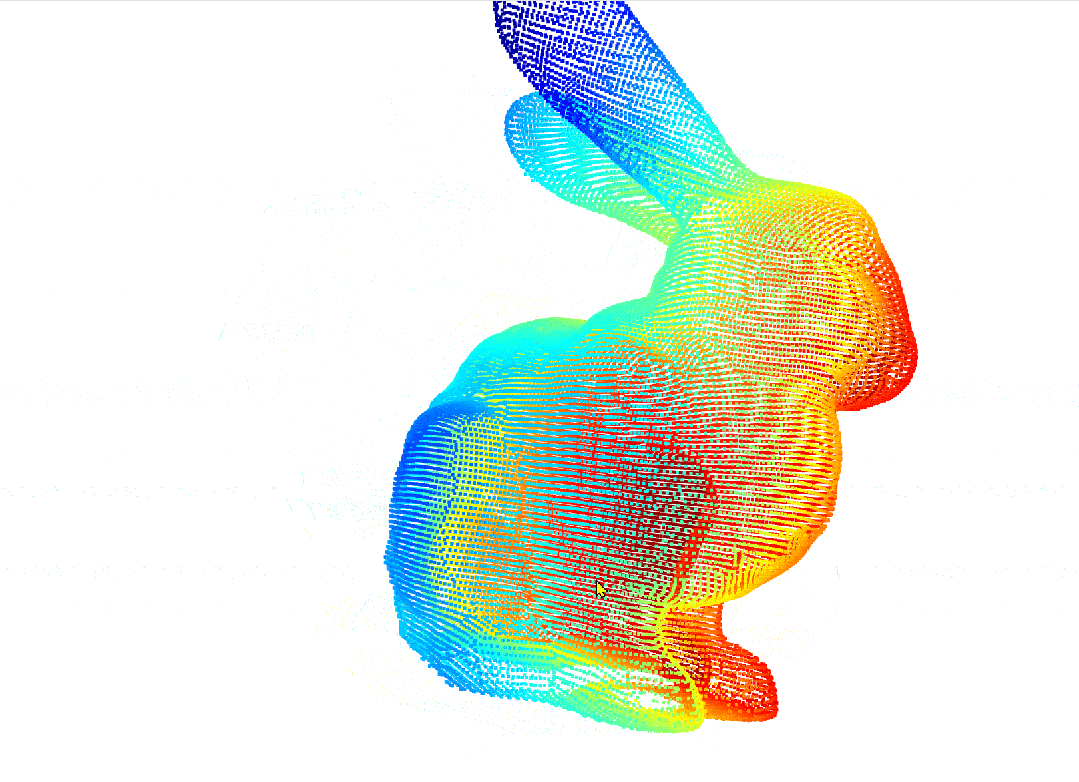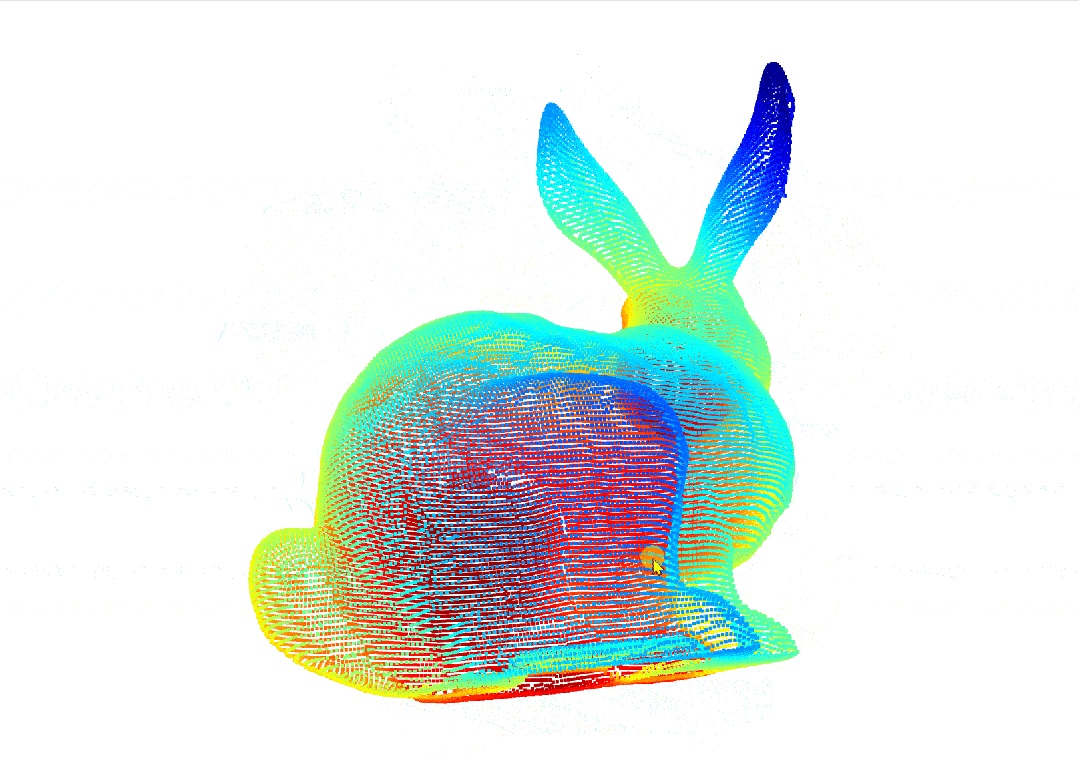
经过PAC处理后的点云:
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!