第28天,贪心算法part02,题目难度在增加,要锻炼贪心思维能力(ง •_•)ง,编程语言:C++
目录
122.买卖股票的最佳时机II
55. 跳跃游戏
45.跳跃游戏II
1005.K次取反后最大化的数组和
总结:
122.买卖股票的最佳时机II
文档讲解:代码随想录买卖股票的最佳时机II
视频讲解:手撕买卖股票的最佳时机II
题目:

学习: 本题最关键的在于理解每天价格之间的关系,事实上从第二天起每一天都会存在利润,只不过有的时候利润是负,有的时候利润是正。因此依据贪心思想,我们收集所有的正利润,得到的就会是最大的利润。不拘泥于选择哪一天买进,而是把每天都作为可能买进,可能卖出的选择,从而收割所有的正利润。
代码:
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int result = 0; //统计利润
//贪心思路,每次只收集正利润
for(int i = 1; i < prices.size(); i++) {
//贪心没有套路,只能靠多了解锻炼
int profit = prices[i] - prices[i - 1];
if(profit > 0) {
result += profit;
}
}
return result;
}
};总结:贪心没有套路,只能通过多练习题目,了解更多的题型,提高贪心的思维能力。
55. 跳跃游戏
文档讲解:代码随想录跳跃游戏
视频讲解:手撕跳跃游戏
题目:

学习:本题不能拘泥在每一步怎么跳上,因为跳跃的方法有很多种,如果关注点在跳多少,怎么跳上就会使得需要遍历的情况很多,并且数组一旦长起来,耗费的时间也会指数增加。
本题的关键在于理解并找到能够跳跃的最大长度(最大覆盖范围),从下标为0开始,我们每走一步确定当前能够到达的最大长度(局部最优),直到最大长度大于等于数组的长度说明能够到达终点,或者是我们遍历能够达到的最大长度后,还是没有达到终点则说明不能到达终点(整体最优)。用图来表示为:
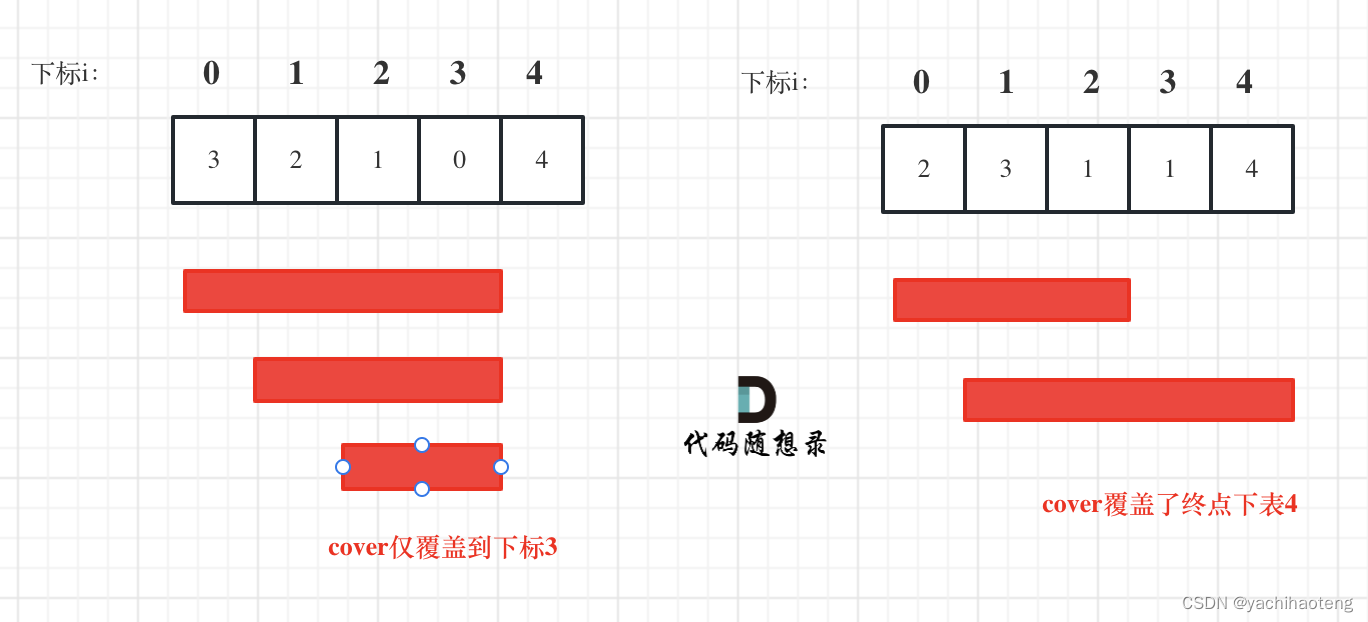
下标 i 在cover范围内移动,每次我们找到了更大的cover,就进行更新。
代码:
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:
bool canJump(vector<int>& nums) {
//贪心策略,找到跳跃的最大覆盖范围
int cover = 0; //初始化覆盖范围
for(int i = 0; i <= cover; i++) {
//更新跳跃的最大覆盖范围
cover = max(cover, i + nums[i]);
//说明覆盖到了最后一个节点
if(maxboard >= nums.size() - 1) return true;
}
return false;
}
};45.跳跃游戏II
文档讲解:代码随想录跳跃游戏II
视频讲解:手撕跳跃游戏II
题目:

学习: 本题与上一题不同的地方在于,本题需要统计走的步数,不能单纯的看覆盖的范围大小了,同时本题题干也说明了一定能够到达最后的位置。
但本题依旧需要用到每一步的覆盖范围,不同的在于,本题需要用一个变量记录前一步覆盖的范围,而遍历过程中下标i超过了覆盖范围时,就说明要走下一步了,此时前一步的覆盖范围就变成了当前的最大覆盖范围,之后依次类推直到找到覆盖范围到达最后的节点。用图来表示为:
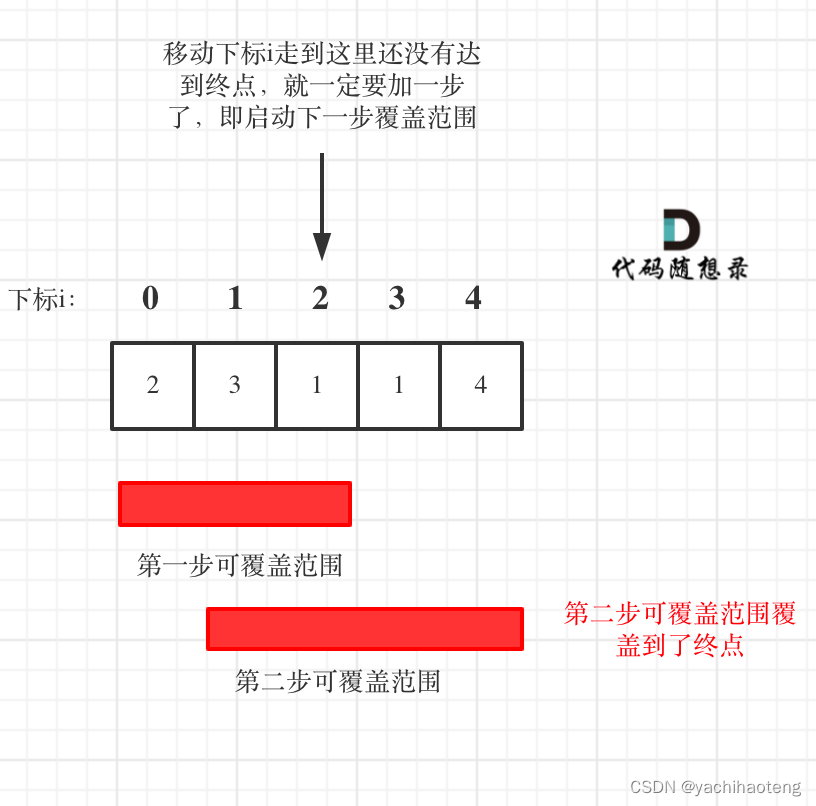
代码:关键在于:1.如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。2.如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:
int jump(vector<int>& nums) {
if (nums.size() == 1) return 0;
int result = 0; //记录跳跃的步数
int precover = 0; //当前覆盖最远距离下标
int cover = 0; //下一步覆盖最远距离下标
for(int i = 0; i < nums.size(); i++) {
cover = max(cover, i + nums[i]);
if(i == precover) {
result++;
precover = cover;
if (precover >= nums.size() - 1) {
return result;
}
}
}
return result;
}
};总结:本题的贪心依旧十分巧妙,理解本题的关键在于: 以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点,这个范围内最少步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
1005.K次取反后最大化的数组和
文档讲解:代码随想录K次取反后最大化的数组和
视频讲解:手撕K次取反后最大化的数组和
题目:

学习:显然本题的贪心想法是很容易能够想到的,本题有两个贪心的部分:1.当数组中存在负数,且k大于0时,我们局部最优就是将绝对值最大的负数进行反转,这样才能够最终得到最大的数组之和。2.当数组中不存在负数后,k还大于0,此时我们局部最优的方式应该是将绝对值最小的正整数(包含0)进行反转,并且只对其进行反转,这样的话如果k为偶数,最后还是只有正整数,如果k为负数,那这个负数也会是绝对值最小的那个,最终就能得到数组和最大。
代码:根据上述贪心逻辑,我们可以写出代码如下,主要注意两点:1.要先对数组进行排序;2.要找到绝对值最小的数,包括从负数变为正数后的那些数。
//时间复杂度O(nlogn)排序算法复杂度
//空间复杂度O(1)
class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
//贪心逻辑,先对负数进行取反(先取反绝对值最小的负数)
//如果k还有剩余,对最小的正数进行取反
sort(nums.begin(), nums.end());
int count = INT_MAX; //记录最小的正数,包括负数变成的正数
int result = 0; //记录最终和
//取反所有负数
for (int i = 0; i < nums.size(); i++) {
if(k > 0 && nums[i] < 0) {
k--;
nums[i] *= -1;
}
count = min(count, nums[i]);
result += nums[i];
}
//如果还有奇数次的k,把最小的正数取反,如果是偶数的k就不用了,因为可以对一个数反复取反
if(k%2 == 1) {
//把最小的正数取反也就意味着减去两倍的count(减去原先的count,再加上负数的count)
result -= count*2;
}
return result;
}
};本题对于排序算法还有可以优化的部分,可以最开始就通过绝对值大小对数组进行排序。最后可以根据以下步骤进行代码编写:
- 第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
- 第二步:从前向后遍历,遇到负数将其变为正数,同时K--
- 第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
- 第四步:求和
代码:
//时间复杂度O(nlogn)
//空间复杂度O(1)
class Solution {
static bool cmp(int a, int b) {
return abs(a) > abs(b);
}
public:
int largestSumAfterKNegations(vector<int>& A, int K) {
sort(A.begin(), A.end(), cmp); // 第一步
for (int i = 0; i < A.size(); i++) { // 第二步
if (A[i] < 0 && K > 0) {
A[i] *= -1;
K--;
}
}
if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步
int result = 0;
for (int a : A) result += a; // 第四步
return result;
}
};总结:
贪心算法,更多的还是考研一个常识性和思维性的东西,需要多加练习,多加锻炼。